二分搜索算法
二分搜索最初是来源于对方程解的思考.
在解决方程式解时可以这样考虑,无论方程对应的曲线走势如何,如果有解的话,那么曲线必然会经过x=0这条直线.
曲线如果经过此直线,且呈现出单调性的话,则可以用"二分"策略予以解决.
具体就是先确定一个包含解的区间,然后二分这个区间,最终把区间缩小到可以满足精度要求即可.
初中课本中就有经典的求2的正根,就是以这种二分的策略进行尝试的.
通常的二分搜索可以极大的减少尝试的次数,缩短时间复杂度为log(n).
/*************以下时牛顿迭代法****************/
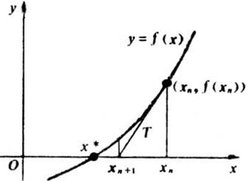
牛顿迭代法可不是用二分来实现的,从上面的图可以看出,只需确定一个曲线上的坐标,然后就可以迭代下去.如果在此点附近有解的话,最终会在根处收敛.
具体的迭代算法,可以百度百科的介绍尝试,这个不难.
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
继续讲二分:
二分搜索.从名字就能看出来,它是用于搜索的,源于其搜索的策略极佳,搜索效率很好. 一般时间复杂度限制高的题都不会卡到二分.
二分应用场景很丰富,不仅限于给处一个数,问它是否已存在? 还能适用于其他有关于固定要求的题型,如:最值,极值,和任意能被确定的,唯一的特征值的搜索
它的代码模式也很模板化,不过要注意,左右区间以及判断依据,别搞错了.
例题:
https://ac.nowcoder.com/acm/contest/1000/A
1 #include <cstdio> 2 #include <iostream> 3 #include<cstring> 4 #include<algorithm> 5 const int N = 100005; 6 int cows[N]; double sum[N]; 7 8 struct node 9 { 10 int i,j; 11 double avg; 12 }no[N]; 13 int n, m,cnt=0; 14 15 bool cmp(const node a,const node b) 16 { 17 return a.avg<a.avg; 18 } 19 void f() 20 { 21 memset(sum,0,sizeof(double)*N); 22 for(int i=1;i<=n;i++) 23 { 24 sum[i]=sum[i-1]+cows[i]; 25 } 26 } 27 28 void init() 29 { 30 for(int i=1;i<=n;i++) 31 { 32 for(int j=i+m-1;j<=n;j++) 33 { 34 no[cnt++]=(node){i,j,(sum[j]-sum[i]+cows[i])*1.0/(j-i+1)}; 35 //if((sum[j]-sum[i]+cows[i])*1ll/(j-i+1)>=avg) return true; 36 } 37 } 38 std::sort(no,no+cnt,cmp); 39 } 40 bool check(double avg) 41 {//检查原奶牛场中是否存在子场序列,其满足长度要求且满足average要求 42 /*for(int i=1;i<=n;i++) 43 { 44 for(int j=i+m-1;j<=n;j++) 45 { 46 if((sum[j]-sum[i]+cows[i])*1ll/(j-i+1)>=avg) return true; 47 } 48 } 49 */ 50 int flag=0; 51 for(int i=0;i<cnt;i++)if(no[i].avg>avg&&no[i].j-no[i].i+1==m) flag=1; 52 if(flag) return true; 53 return false; 54 55 56 57 //return false; 58 } 59 60 int main() { 61 scanf("%d %d", &n, &m); 62 double l = 0, r = 0; 63 for (int i = 1; i <= n; i++) { 64 scanf("%d", &cows[i]); 65 r = std::max(r, (double)cows[i]); 66 } 67 f(); 68 init(); 69 while(r - l > 1e-5) {//以前这里我看成了r-1就导致了失误,结果是l。。。 70 double mid = (l + r) / 2; 71 if(check(mid)) l = mid; 72 else r = mid; 73 } printf("%d\n", (int)(r * 1000)); 74 return 0; 75 }
例题是让我们求一个数列中满足一定条件的子数列的最大平均值大小?
从问题可以料想,这个数列中的这个子数列的最大平均值肯定是唯一的,不可能存在a是最大平均值,也存在一个不等于a的b,使得b也是最大平均值!
所以通常最能想到的解法就是枚举每一个子数列,找出最大的平均值.
不过这样效率低,所以就可以通过对这个平均值量进行二分搜索.
对每一个当前平均值,我们有:
如果存在比它大的子数列平均值,则解区间向右压缩一半
否则,解区间向左压缩一半
知道解出答案为止.
注意:解题时,题意简化很重要.



