西瓜书课后习题——第四章

4.1

不含有特征向量相同但标记不同的冲突数据 and 决策树按照属性特征来划分，相同属性特征的样本最终会进入同一个叶子节点 >- 如果含有特征向量相同但标记不同的冲突数据 >- 必然至少存在一对样本，属性相同而分类不同，即产生了训练误差 >- 不含有特征向量相同但标记不同的冲突数据

4.2

简单的使用最小误差原理会导致机器学习产生严重的过拟合，严重影响机器学习的泛化能力。

4.3

信息熵（香农熵）计算公式为   $Ent(D)=-\sum_{k=1}^{|y|}p_{k}log_{2}p_{k}$  其中，$p_{k}$是当前样本集合D中第k类样本所占比例，|y|代表共有多少类样本，计算香农熵主要就是计算$p_{k}=\frac{第k类样本的数量}{样本总数}$ ，而第k类样本的数量可以通过建立字典来统计，样本总数就简单了。

香农熵的实现代码：

def calcShannoEnt(dataset):
    from math import log
    total_number = len(dataset)
    label_dict = {}
    for data_line in dataset:
        label = data_line[-1]
        label_dict[label] = label_dict.get(label,0) + 1
    #计算香农熵
    ShannoEnt = 0
    for key in label_dict.keys():
        prob = float(label_dict[key]) / total_number
        ShannoEnt -= prob * log(prob, 2)
    return ShannoEnt

R代码
library(rpart)
data <- read.csv('/home/zwt/PycharmProjects/test/data/data_4.3.csv')
data <- data[-1] #删除编号
data
dtree <- rpart(好瓜~., data = data, method = 'class', parms = list(split = 'information'),control=list(minsplit=1,minbucket=round(1/3)))
printcp(dtree)
print(dtree)
opar<-par(no.readonly = T)
par(mfrow=c(1,2))
library(rpart.plot)
png(file='/home/zwt/PycharmProjects/test/Machine_Learning/课后题/tree.png')
rpart.plot(dtree,branch=1,type=4,fallen.leaves=T,cex=0.8,sub='剪枝前')
par(opar)
dev.off()

4.4

 

R代码
library(rpart)
data <- read.csv('/home/zwt/PycharmProjects/test/data/data_4.2.csv')
data <- data[-1] #删除编号
data
#未剪枝
dtree <- rpart(好瓜~., data = data, method = 'class', parms = list(split = 'gini'), control = list(minsplit=1,minbucket=round(1/3)))
printcp(dtree)
print(dtree)
#剪枝(未区分预剪枝和后剪枝)
#查看上一步dtree的结果发现xerror最小对应的CP值为0.125，因此可以指定cp=0.125进行剪枝
#xtree<-prune(dtree,cp=0.125)
#也可以编写通用函数选择xerror最小的CP值进行剪枝
tree<-prune(dtree,cp=dtree$cptable[which.min(dtree$cptable[,"xerror"]),"CP"])
opar<-par(no.readonly = T)
par(mfrow=c(1,2))
library(rpart.plot)
png(file='/home/zwt/PycharmProjects/test/Machine_Learning/课后题/tree4.4.1.png')
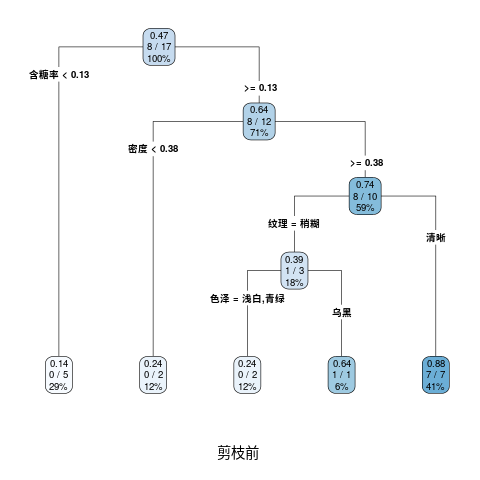
rpart.plot(dtree,branch=1,type=4,fallen.leaves=T,cex=0.8,sub='剪枝前')
png(file = "/home/zwt/PycharmProjects/test/Machine_Learning/课后题/tree4.4.2.png")
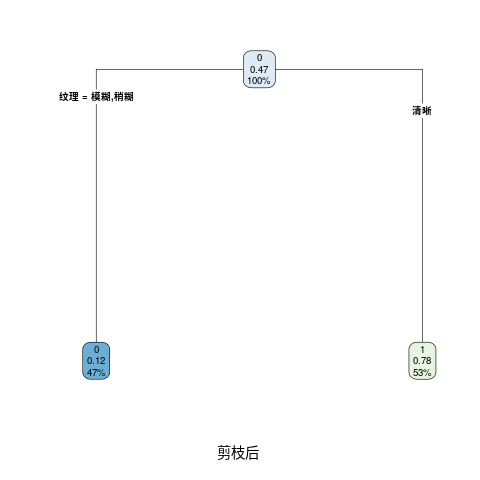
rpart.plot(xtree,branch=1, type=4,fallen.leaves=T,cex=0.8, sub="剪枝后")
par(opar)
dev.off()

 

 

4.5

 

R代码
library(rpart)
data <- read.csv('/home/zwt/PycharmProjects/test/data/data_4.3.csv')
data <- data[-1] #删除编号
data
dtree <- rpart(好瓜~., data = data, method = 'poisson', control=list(minsplit=1,minbucket=round(1/3)))
printcp(dtree)
print(dtree)
opar<-par(no.readonly = T)
par(mfrow=c(1,2))
library(rpart.plot)
png(file='/home/zwt/PycharmProjects/test/Machine_Learning/课后题/tree4.5.png')
rpart.plot(dtree,branch=1,type=4,fallen.leaves=T,cex=0.8,sub='剪枝前')
par(opar)
dev.off()

 

4.6

UCI数据集

4.7

直接递归会导致大量的临时变量被存储，层数过深时会导致“栈”溢出。用队列进行层次遍历生成决策树，用Max_Depth来控制决策树的最大深度，队列中每个元素代表着决策树的每个节点，它必要的属性有：样本集合、剩余属性集合、当前层数标记、父节点序号。队列开始只有一个元素，就是最初的状态，带着所有样本的根节点。然后当队列不为空的时候开始循环，每次取出一个元素来判断是否需要划分，如果不需要，该元素就变成一个叶节点，弹出队列就不用再管了；如果需要划分就找出最好的划分属性，然后分成n个子区间，依次送入队列，继续循环，直到队列为空。

是否需要划分有三个依据：当前所有样本属于一类、当前所有样本属性完全相同、达到Max_Depth

这样即完成了层次遍历(广度优先搜索)决策树的构建。

显然由于每次出队列的元素要先完全划分，所以进行的是预剪枝算法，队列结构很方便，如果是后剪枝，必须要等到决策树完全生成才能进行。

4.8

4.9

4.10