西瓜书课后习题——第三章
3.1
式3.2 $f(x)=\omega ^{T}x+b$ 中,$\omega ^{T}$ 和b有各自的意义,简单来说,$\omega ^{T}$ 决定学习得到模型(直线、平面)的方向,而b则决定截距,当学习得到的模型恰好经过原点时,可以不考虑偏置项b。偏置项b实质上就是体现拟合模型整体上的浮动,可以看做是其它变量留下的偏差的线性修正,因此一般情况下是需要考虑偏置项的。但如果对数据集进行了归一化处理,即对目标变量减去均值向量,此时就不需要考虑偏置项了。
3.2
对区间[a,b]上定义的函数f(x),若它对区间中任意两点x1,x2均有$f(\frac{x1+x2}{2})\leq \frac{f(x1)+f(x2)}{2}$,则称f(x)为区间[a,b]上的凸函数。对于实数集上的函数,可通过二阶导数来判断:若二阶导数在区间上非负,则称为凸函数,在区间上恒大于零,则称为严格凸函数。
对于式3.18 $y=\frac{1}{1+e^{-(\omega ^{T}x+b)}}$,有
$\frac{dy}{d\omega ^{T}}=\frac{1}{(1+e^{-(\omega ^{T}x+b)})^{2}}e^{-(\omega ^{T}x+b)}(-x)=(-x)\frac{1}{1+e^{-(\omega ^{T}x+b)}}(1-\frac{1}{1+e^{-(\omega ^{T}x+b)}})=xy(y-1)=x(y^{2}-y)$
$\frac{d}{d\omega ^{T}}(\frac{dy}{d\omega ^{T}})=x(2y-1)(\frac{dy}{d\omega ^{T}})=x^{2}y(2y-1)(y-1)$
其中,y的取值范围是(0,1),不难看出二阶导有正有负,所以该函数非凸。
3.3
对率回归即Logis regression
西瓜集数据如图所示:
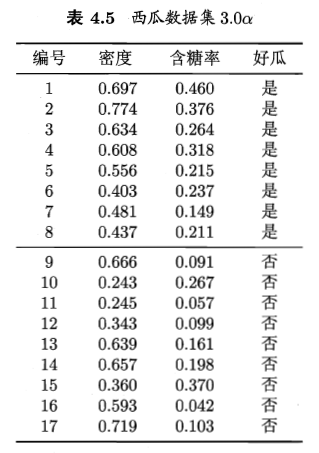
将好瓜这一列变量用0/1变量代替,进行对率回归学习,python代码如下:

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
dataset = pd.read_csv('/home/zwt/Desktop/watermelon3a.csv')
#数据预处理
X = dataset[['密度','含糖率']]
Y = dataset['好瓜']
good_melon = dataset[dataset['好瓜'] == 1]
bad_melon = dataset[dataset['好瓜'] == 0]
#画图
f1 = plt.figure(1)
plt.title('watermelon_3a')
plt.xlabel('density')
plt.ylabel('radio_sugar')
plt.xlim(0,1)
plt.ylim(0,1)
plt.scatter(bad_melon['密度'],bad_melon['含糖率'],marker='o',color='r',s=100,label='bad')
plt.scatter(good_melon['密度'],good_melon['含糖率'],marker='o',color='g',s=100,label='good')
plt.legend(loc='upper right')
#分割训练集和验证集
X_train,X_test,Y_train,Y_test = model_selection.train_test_split(X,Y,test_size=0.5,random_state=0)
#训练
log_model = LogisticRegression()
log_model.fit(X_train,Y_train)
#验证
Y_pred = log_model.predict(X_test)
#汇总
print(metrics.confusion_matrix(Y_test, Y_pred))
print(metrics.classification_report(Y_test, Y_pred, target_names=['Bad','Good']))
print(log_model.coef_)
theta1, theta2 = log_model.coef_[0][0], log_model.coef_[0][1]
X_pred = np.linspace(0,1,100)
line_pred = theta1 + theta2 * X_pred
plt.plot(X_pred, line_pred)
plt.show()

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
dataset = pd.read_csv('/home/zwt/Desktop/watermelon3a.csv')
#数据预处理
X = dataset[['密度','含糖率']]
Y = dataset['好瓜']
good_melon = dataset[dataset['好瓜'] == 1]
bad_melon = dataset[dataset['好瓜'] == 0]
#画图
f1 = plt.figure(1)
plt.title('watermelon_3a')
plt.xlabel('density')
plt.ylabel('radio_sugar')
plt.xlim(0,1)
plt.ylim(0,1)
plt.scatter(bad_melon['密度'],bad_melon['含糖率'],marker='o',color='r',s=100,label='bad')
plt.scatter(good_melon['密度'],good_melon['含糖率'],marker='o',color='g',s=100,label='good')
plt.legend(loc='upper right')
#分割训练集和验证集
X_train,X_test,Y_train,Y_test = model_selection.train_test_split(X,Y,test_size=0.5,random_state=0)
#训练
log_model = LogisticRegression()
log_model.fit(X_train,Y_train)
#验证
Y_pred = log_model.predict(X_test)
#汇总
print(metrics.confusion_matrix(Y_test, Y_pred))
print(metrics.classification_report(Y_test, Y_pred))
print(log_model.coef_)
theta1, theta2 = log_model.coef_[0][0], log_model.coef_[0][1]
X_pred = np.linspace(0,1,100)
line_pred = theta1 + theta2 * X_pred
plt.plot(X_pred, line_pred)
plt.show()
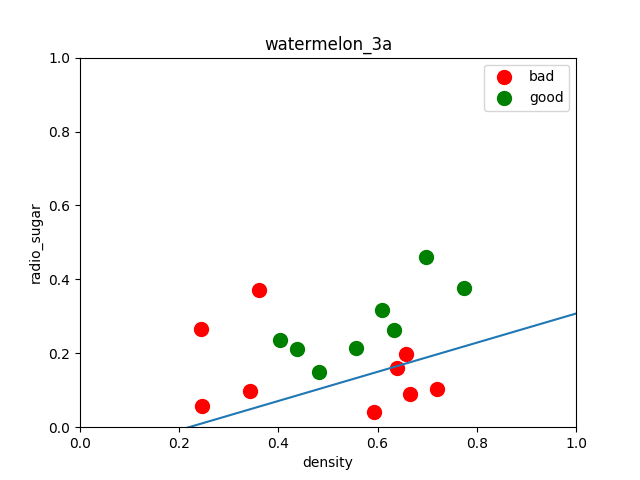
模型效果输出(查准率、查全率、预测效果评分):
precision recall f1-score support
Bad 0.75 0.60 0.67 5
Good 0.60 0.75 0.67 4
micro avg 0.67 0.67 0.67 9
macro avg 0.68 0.68 0.67 9
weighted avg 0.68 0.67 0.67 9
也可以输出验证集的实际结果和预测结果:
密度 含糖率 Y_test Y_pred
1 0.774 0.376 1 1
6 0.481 0.149 1 0
8 0.666 0.091 0 0
9 0.243 0.267 0 1
13 0.657 0.198 0 0
4 0.556 0.215 1 1
2 0.634 0.264 1 1
14 0.360 0.370 0 1
10 0.245 0.057 0 0
3.4
首先附上使用葡萄酒品质数据做的对率回归学习代码

import numpy as np import matplotlib.pyplot as plt import pandas as pd pd.set_option('display.max_rows',None) pd.set_option('max_colwidth',200) pd.set_option('expand_frame_repr', False) from sklearn import model_selection from sklearn.linear_model import LogisticRegression from sklearn import metrics dataset = pd.read_csv('/home/zwt/Desktop/winequality-red_new.csv') #数据预处理 dataset['quality2'] = dataset['quality'].apply(lambda x: 0 if x < 5 else 1) #新加入二分类变量是否为好酒,基于原数据中quality的值,其大于等于5就定义为好酒,反之坏酒 X = dataset[["fixed_acidity","volatile_acidity","citric_acid","residual_sugar","chlorides","free_sulfur_dioxide","total_sulfur_dioxide","density","pH","sulphates","alcohol"]] Y = dataset["quality2"] #分割训练集和验证集 X_train,X_test,Y_train,Y_test = model_selection.train_test_split(X,Y,test_size=0.5,random_state=0) #训练 log_model = LogisticRegression() log_model.fit(X_train,Y_train) #验证 Y_pred = log_model.predict(X_test) #汇总 print(metrics.confusion_matrix(Y_test, Y_pred)) print(metrics.classification_report(Y_test, Y_pred)) print(log_model.coef_)
其中,从UCI下载的数据集格式有问题,无法直接使用,先编写程序将格式调整完毕再使用数据

fr = open('/home/zwt/Desktop/winequality-red.csv','r',encoding='utf-8')
fw = open('/home/zwt/Desktop/winequality-red_new.csv','w',encoding='utf-8')
f = fr.readlines()
for line in f:
line = line.replace(';',',')
fw.write(line)
fr.close()
fw.close()
两种方法的错误率比较

from sklearn.linear_model import LogisticRegression from sklearn import model_selection from sklearn.datasets import load_wine # 载入wine数据 dataset = load_wine() #10次10折交叉验证法生成训练集和测试集 def tenfolds(): k = 0 truth = 0 while k < 10: kf = model_selection.KFold(n_splits=10, random_state=None, shuffle=True) for x_train_index, x_test_index in kf.split(dataset.data): x_train = dataset.data[x_train_index] y_train = dataset.target[x_train_index] x_test = dataset.data[x_test_index] y_test = dataset.target[x_test_index] # 用对率回归进行训练,拟合数据 log_model = LogisticRegression() log_model.fit(x_train, y_train) # 用训练好的模型预测 y_pred = log_model.predict(x_test) for i in range(len(x_test)): #这里和留一法不同,是因为10折交叉验证的验证集是len(dataset.target)/10,验证集的预测集也是,都是一个列表,是一串数字,而留一法是一个数字 if y_pred[i] == y_test[i]: truth += 1 k += 1 # 计算精度 accuracy = truth/(len(x_train)+len(x_test)) #accuracy = truth/len(dataset.target) print("用10次10折交叉验证对率回归的精度是:", accuracy) tenfolds() #留一法 def leaveone(): loo = model_selection.LeaveOneOut() i = 0 true = 0 while i < len(dataset.target): for x_train_index, x_test_index in loo.split(dataset.data): x_train = dataset.data[x_train_index] y_train = dataset.target[x_train_index] x_test = dataset.data[x_test_index] y_test = dataset.target[x_test_index] # 用对率回归进行训练,拟合数据 log_model = LogisticRegression() log_model.fit(x_train, y_train) # 用训练好的模型预测 y_pred = log_model.predict(x_test) if y_pred == y_test: true += 1 i += 1 # 计算精度 accuracy = true / len(dataset.target) print("用留一法验证对率回归的精度是:", accuracy) leaveone()
3.5

import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn import model_selection from sklearn import metrics dataset = pd.read_csv('/home/zwt/Desktop/watermelon3a.csv') #数据预处理 X = dataset[['密度','含糖率']] Y = dataset['好瓜'] #分割训练集和验证集 X_train,X_test,Y_train,Y_test = model_selection.train_test_split(X,Y,test_size=0.5,random_state=0) #训练 LDA_model = LinearDiscriminantAnalysis() LDA_model.fit(X_train,Y_train) #验证 Y_pred = LDA_model.predict(X_test) #汇总 print(metrics.confusion_matrix(Y_test, Y_pred)) print(metrics.classification_report(Y_test, Y_pred, target_names=['Bad','Good'])) print(LDA_model.coef_) #画图 good_melon = dataset[dataset['好瓜'] == 1] bad_melon = dataset[dataset['好瓜'] == 0] plt.scatter(bad_melon['密度'],bad_melon['含糖率'],marker='o',color='r',s=100,label='bad') plt.scatter(good_melon['密度'],good_melon['含糖率'],marker='o',color='g',s=100,label='good')

import numpy as np import matplotlib.pyplot as plt data = [[0.697, 0.460, 1], [0.774, 0.376, 1], [0.634, 0.264, 1], [0.608, 0.318, 1], [0.556, 0.215, 1], [0.403, 0.237, 1], [0.481, 0.149, 1], [0.437, 0.211, 1], [0.666, 0.091, 0], [0.243, 0.267, 0], [0.245, 0.057, 0], [0.343, 0.099, 0], [0.639, 0.161, 0], [0.657, 0.198, 0], [0.360, 0.370, 0], [0.593, 0.042, 0], [0.719, 0.103, 0]] #数据集按瓜好坏分类 data = np.array([i[:-1] for i in data]) X0 = np.array(data[:8]) X1 = np.array(data[8:]) #求正反例均值 miu0 = np.mean(X0, axis=0).reshape((-1, 1)) miu1 = np.mean(X1, axis=0).reshape((-1, 1)) #求协方差 cov0 = np.cov(X0, rowvar=False) cov1 = np.cov(X1, rowvar=False) #求出w S_w = np.mat(cov0 + cov1) Omiga = S_w.I * (miu0 - miu1) #画出点、直线 plt.scatter(X0[:, 0], X0[:, 1], c='b', label='+', marker = '+') plt.scatter(X1[:, 0], X1[:, 1], c='r', label='-', marker = '_') plt.plot([0, 1], [0, -Omiga[0] / Omiga[1]], label='y') plt.xlabel('密度', fontproperties='SimHei', fontsize=15, color='green'); plt.ylabel('含糖率', fontproperties='SimHei', fontsize=15, color='green'); plt.title(r'LinearDiscriminantAnalysis', fontproperties='SimHei', fontsize=25); plt.legend() plt.show()
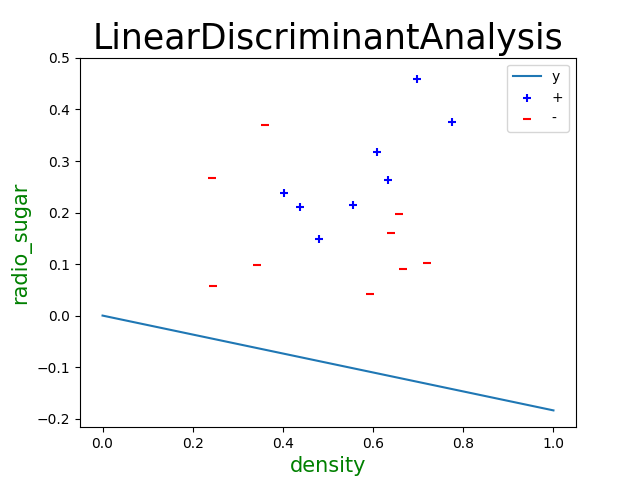
3.6
对于非线性可分的数据,要想使用判别分析,一般思想是将其映射到更高维的空间上,使它在高维空间上线性可分进一步使用判别分析。
3.7
3.8
理论上的(纠错输出码)ECOC码能理想纠错的重要条件是每个码位出错的概率相当,因为如果某个码位的错误率很高,会导致这位始终保持相同的结果,不再有分类作用,这就相当于全0或者全 1的分类器。
3.9
书中提到,对于OvR,MvM来说,由于对每个类进行了相同的处理,其拆解出的二分类任务中类别不平衡的影响会相互抵消,因此通常不需要专门处理。以ECOC编码为例,每个生成的二分类器会将所有样本分成较为均衡的二类,使类别不平衡的影响减小。当然拆解后仍然可能出现明显的类别不平衡现象,比如一个超级大类和一群小类。
3.10
数据集(密码rw81)



