数据结构
线性表
线性表的顺序表示
静态分配
#define MaxSize 10 // 定义最大长度
typedef struct {
int data[MaxSize]; // ElemType = int, * 用静态的“数组”存访数据元素
int length; // 顺序表的当前长度
} SqList;
动态分配
#define InitSize 10 // 顺序表的初始长度
typedef struct {
int * data; // ElemType = int, * 声明动态分配数组的指针
int MaxSize; // 顺序表的最大容量
int length; // 顺序表的当前长度
} SqList;
// 初始化顺序表
void InitList(SqList &L) {
// 用 malloc 函数申请一片连续的存储空间
L.data = (int *)malloc(InitSize * sizeof(int));
L.length = 0;
L.MaxSize = InitSize;
}
特点:
- 可随机访问,查找元素所需时间复杂度为
O(1)。 - 存储密度高,每个节点只存储数据元素。
- 拓展容量不方便(即使使用动态分配的方式实现,拓展长度的时间复杂度也比较高,因为需要把数据复制到新的区域)。
- 插入删除操作不方便,需移动大量元素:
O(n)。
线性表的链式表示
单链表
struct LNode{ //定义单链表节点类型 LNode:结点
ElemType data; //每个结点存放一个数据元素 data:数据域
struct LNode *next; //指针指向下一个结点 next:指针域
};
双链表
typedef struct DNode{ //定义双链表结点类型
ElemType data; //数据域
struct DNode *prior, *next; //前驱和后继指针
}DNode, *DLinklist;
循环单链表
最后一个结点的指针不是NULL,而是指向头结点
循环双链表
表头结点的prior指向表尾结点,表尾结点的next指向头结点
静态链表
#define MaxSize 10 //静态链表的最大长度
typedef struct{ //静态链表结构类型的定义
ELemType data; //存储数据元素
int next; //下一个元素的数组下标
}SLinkList[MaxSize];
void testSLinkList(){
SLinkList a;
}
栈 (stack)
栈是特殊的线性表:只允许在一端进行插入或删除操作, 其逻辑结构与普通线性表相同
栈顶:允许进行插入和删除的一端 (最上面的为栈顶元素)
栈底:不允许进行插入和删除的一端 (最下面的为栈底元素)
空栈:不含任何元素的空表
特点:后进先出(后进栈的元素先出栈)
缺点:栈的大小不可变,解决方法——共享栈
栈的顺序存储
#define MaxSize 10 //定义栈中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //静态数组存放栈中元素
int top; //栈顶元素
}SqStack;
void testStack(){
SqStack S; //声明一个顺序栈(分配空间)
//连续的存储空间大小为 MaxSize*sizeof(ElemType)
}
栈的链式存储结构
因此,链栈实际上就是一个只能采用头插法插入或删除数据的链表
typedef struct Linknode{
ElemType data; //数据域
struct Linknode *next; //指针域
}*LiStack; //栈类型的定义
应用
- 栈在括号匹配中的应用
- 中缀表达式 (需要界限符)
- 后缀表达式 (逆波兰表达式)
- 栈在递归中的应用
队列(Queue)
- 队列是操作受限的线性表,只允许在一端进行插入 (入队),另一端进行删除 (出队)
- 操作特性:先进先出 FIFO
- 队头:允许删除的一端
- 队尾:允许插入的一端
- 空队列:不含任何元素的空表
# define MaxSize 10; //定义队列中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //用静态数组存放队列元素
//连续的存储空间,大小为——MaxSize*sizeof(ElemType)
int front, rear; //队头指针和队尾指针
}SqQueue;
- 队头指针:指向队头元素;
- 队尾指针:指向队尾元素的后一个位置(下一个应该插入的位置)
循环队列(判满)
方案一: 牺牲一个单元来区分队空和队满
队尾指针的再下一个位置就是队头,即 (Q.rear+1)%MaxSize == Q.front
- 循环队列——入队:只能从队尾插入(判满使用方案一)
bool EnQueue(SqQueue &Q, ElemType x){
if((Q.rear+1)%MaxSize == Q.front) //队满
return false;
Q.data[Q.rear] = x; //将x插入队尾
Q.rear = (Q.rear + 1) % MaxSize; //队尾指针加1取模
return true;
}
- 循环队列——出队:只能让队头元素出队
//出队,删除一个队头元素,用x返回
bool DeQueue(SqQueue &Q, ElemType &x){
if(Q.rear == Q.front) //队空报错
return false;
x = Q.data[Q.front];
Q.front = (Q.front + 1) % MaxSize; //队头指针后移动
return true;
}
- 循环队列——获得队头元素
bool GetHead(SqQueue &Q, ElemType &x){
if(Q.rear == Q.front) //队空报错
return false;
x = Q.data[Q.front];
return true;
}
方案二: 不牺牲存储空间,设置size
定义一个变量 size用于记录队列此时记录了几个数据元素,初始化 size = 0,进队成功 size++,出队成功size--,根据size的值判断队满与队空
队满条件:size == MaxSize
队空条件:size == 0
方案三: 不牺牲存储空间,设置tag
定义一个变量 tag,tag = 0 --最近进行的是删除操作;tag = 1 --最近进行的是插入操作;
每次删除操作成功时,都令tag = 0;只有删除操作,才可能导致队空;
每次插入操作成功时,都令tag = 1;只有插入操作,才可能导致队满;
队满条件:Q.front == Q.rear && tag == 1
队空条件:Q.front == Q.rear && tag == 0
队列的链式存储结构
typedef struct LinkNode{ //链式队列结点
ElemType data;
struct LinkNode *next;
}
typedef struct{ //链式队列
LinkNode *front, *rear; //队列的队头和队尾指针
}LinkQueue;
双端队列
- 双端队列允许从两端插入、两端删除的线性表;
- 如果只使用其中一端的插入、删除操作,则等同于栈;
- 输入受限的双端队列:允许一端插入,两端删除的线性表;
- 输出受限的双端队列:允许两端插入,一端删除的线性表;
串
顺序表
#define MAXLEN 255 //预定义最大串长为255
typedef struct{
char ch[MAXLEN]; //静态数组实现(定长顺序存储)
//每个分量存储一个字符
//每个char字符占1B
int length; //串的实际长度
}SString;
堆分配
//动态数组实现
typedef struct{
char *ch; //按串长分配存储区,ch指向串的基地址
int length; //串的长度
}HString;
HString S;
S.ch = (char *) malloc(MAXLINE * sizeof(char)); //基地址指针指向连续空间的起始位置
//malloc()需要手动free()
S.length;
链式存储
typedef struct StringNode{
char ch; //每个结点存1个字符
struct StringNode *next;
}StringNode, * String;
树
顺序存储
#define MaxSize 100
struct TreeNode{
ElemType value; //结点中的数据元素
bool isEmpty; //结点是否为空
}
链式存储
//二叉树的结点
struct ElemType{
int value;
};
typedef struct BiTnode{
ElemType data; //数据域
struct BiTNode *lchild, *rchild; //左、右孩子指针
}BiTNode, *BiTree;
计算机科学中的树
| 二叉树 | ▪ 二叉树▪ 二叉查找树▪ 笛卡尔树▪ [Top tree](http://baike.baidu.com/searchword/?word=Top tree&pic=1&sug=1&enc=utf8)▪ T树 |
|---|---|
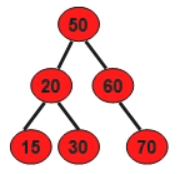
二叉查找树
中序有序
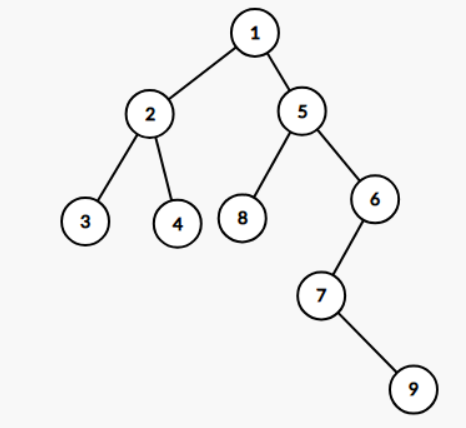
笛卡尔树
范围最值查询与最低公共祖先( 距离两个节点最近的共同祖先 )
| 自平衡二叉查找树 | ▪ AA树▪ AVL树▪ 红黑树▪ 伸展树▪ 树堆▪ 节点大小平衡树 |
|---|---|
AVL树
本质上还是一棵二叉搜索树,它的特点是:
1.本身首先是一棵二叉搜索树。
2.带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
也就是说,AVL树,本质上是带了平衡功能的二叉查找树(二叉排序树,二叉搜索树)。
红黑树
是一种特化的AVL树 , 它可以在O(log n)时间内做查找,插入和删除
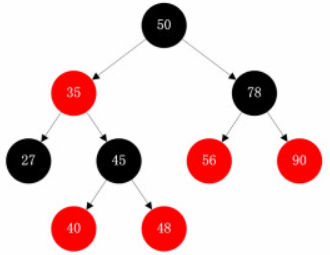
在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
性质1. 结点是红色或黑色。
性质2. 根结点是黑色。
性质3. 所有叶子都是黑色。(叶子是NIL结点)
性质4. 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
性质5. 从任一节结点其每个叶子的所有路径都包含相同数目的黑色结点。
这些约束强制了红黑树的关键性质:
从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。
结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例。
这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
| B树 | B树 B+树 B*树 Bx树 UB树 2-3树 2-3-4树 |
|---|---|
B树(B-)
而B-树查询时间复杂度不固定,与 key 在树中的位置有关,最好为O(1)。
B-树,这里的 B 表示 balance( 平衡的意思),B-树是一种多路自平衡的搜索树
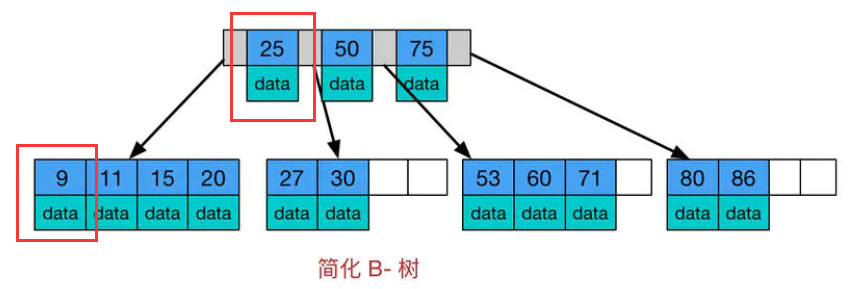
B-树有如下特点:
- 所有键值分布在整颗树中(索引值和具体data都在每个节点里);
- 任何一个关键字出现且只出现在一个结点中;
- 搜索有可能在非叶子结点结束(最好情况O(1)就能找到数据);
- 在关键字全集内做一次查找,性能逼近二分查找;
B-树是专门为外部存储器设计的,如磁盘,它对于读取和写入大块数据有良好的性能,所以一般被用在文件系统及数据库中。
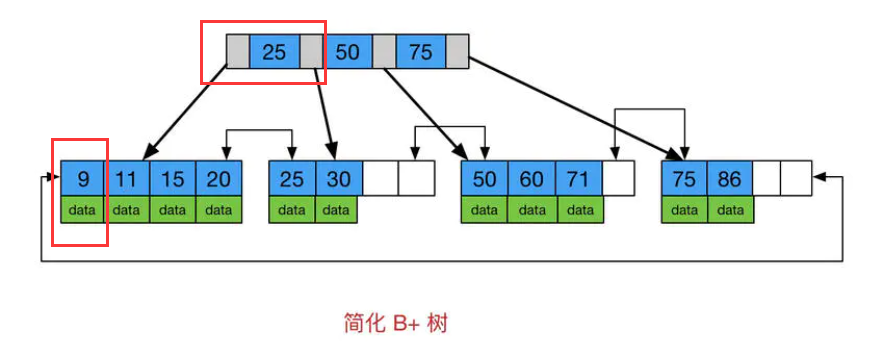
B+ 树
时间复杂度固定为 log n
| Trie | ▪ 前缀树▪ 后缀树▪ 基数树 |
|---|---|
| 空间划分树 | ▪ 四叉树▪ 八叉树▪ k-d树▪ vp-树▪ R树▪ R*树▪ R+树▪ X树▪ M树▪ 线段树▪ 希尔伯特R树▪ 优先R树 |
|---|---|
算法
typora插入动图技巧 <img src="图片地址" style="zoom: 100%" />
冒泡排序
对一个列表多次重复遍历。它要比较相邻的两项,并且交换顺序
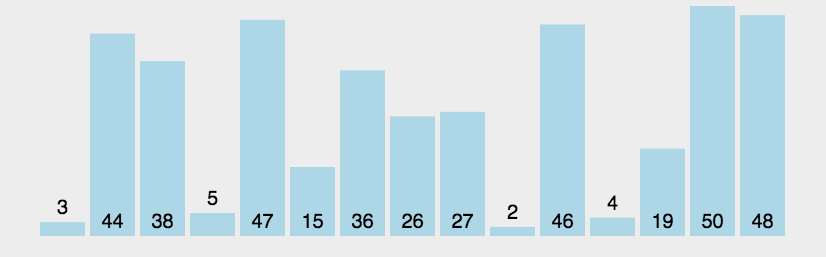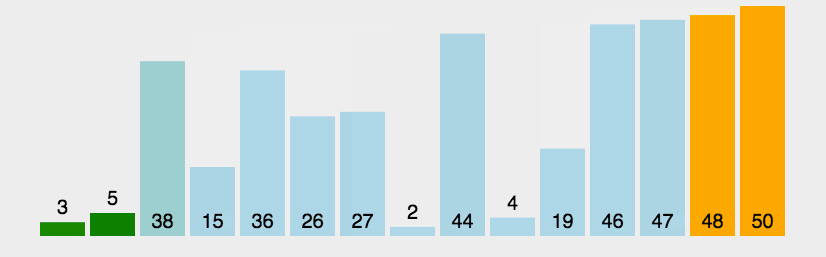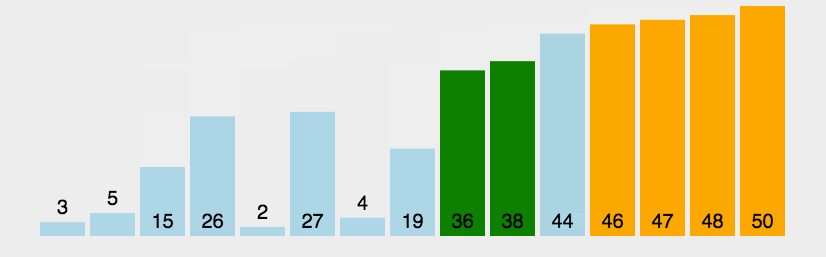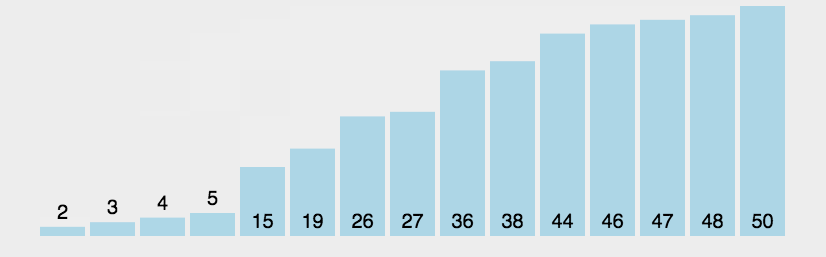
选择排序
每遍历一次列表只交换一次数据将它换到正确的位置 。
一共需要 n-1 次遍历来排好 n 个数据 。
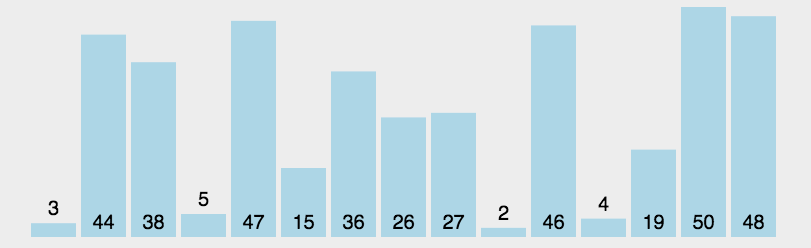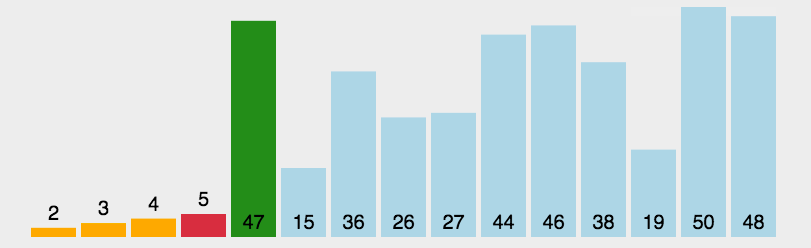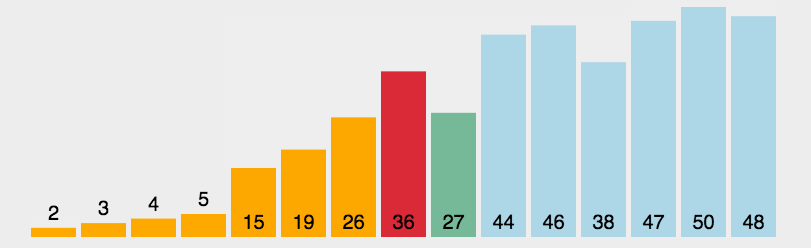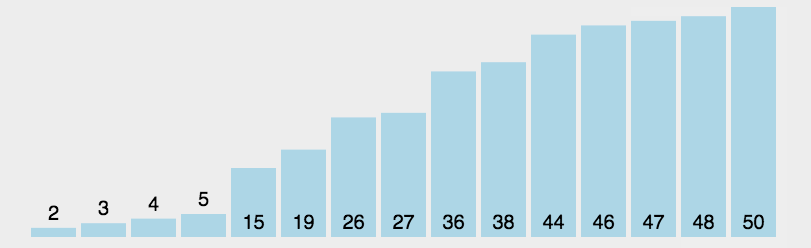
插入排序
每一个新的数据项被 插入到前边的子表里
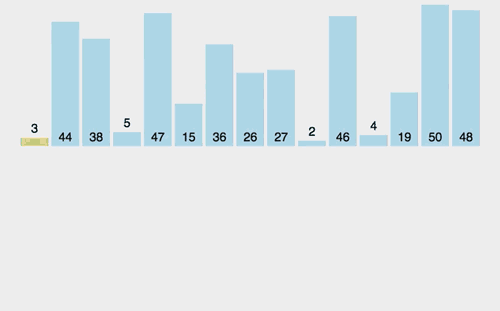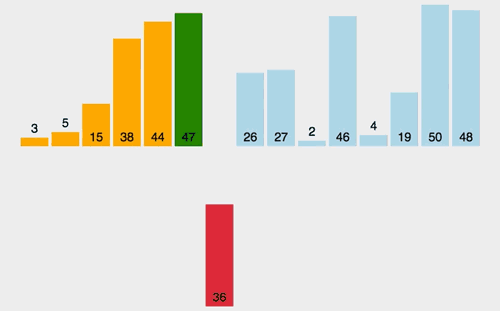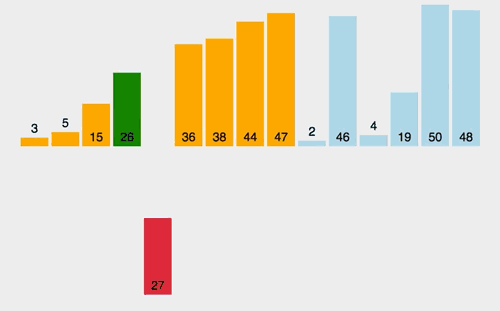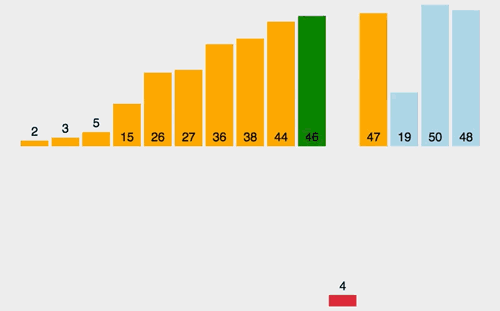
希尔排序
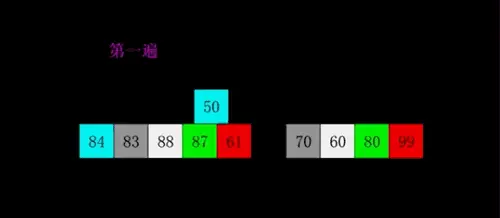
缩小间隔排序
它以插入排序为基础,将原来要排序的列表划分为一些子列表,再对每一个子列表执行插入排序 。
归并排序
把两个排序好了的列表结合在一起组合成一个单一的有序的新列表
归并排序是一种递归算法,它持续地将一个列表分成两半
如果列表是空的或者 只有一个元素,那么根据定义,它就被排序好了(最基本的情况 )
如果列表里的元素超过一个,我们就把列表拆分,然后分别对两个部分调用递归排序。
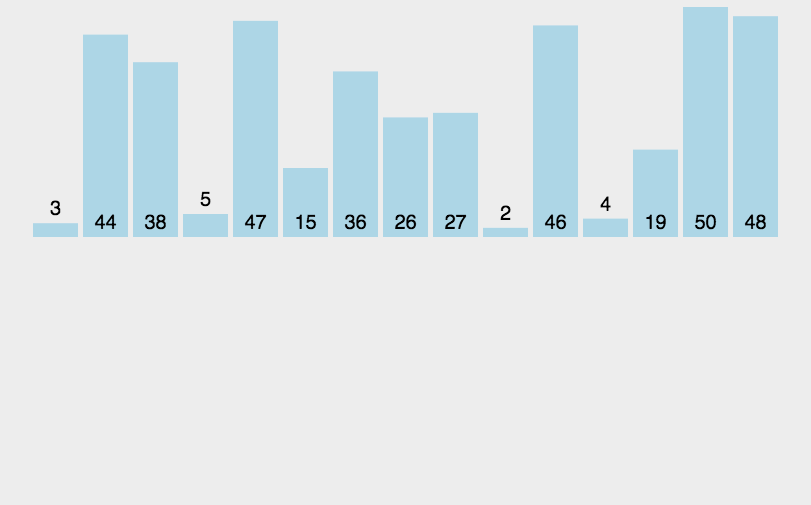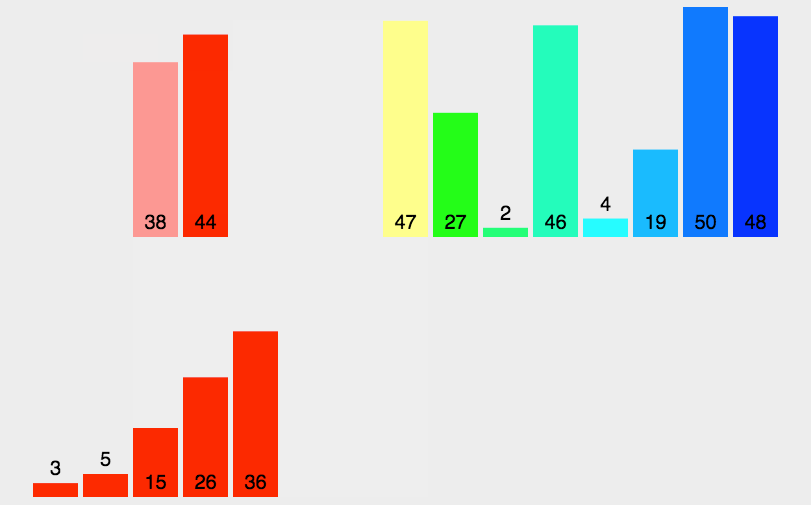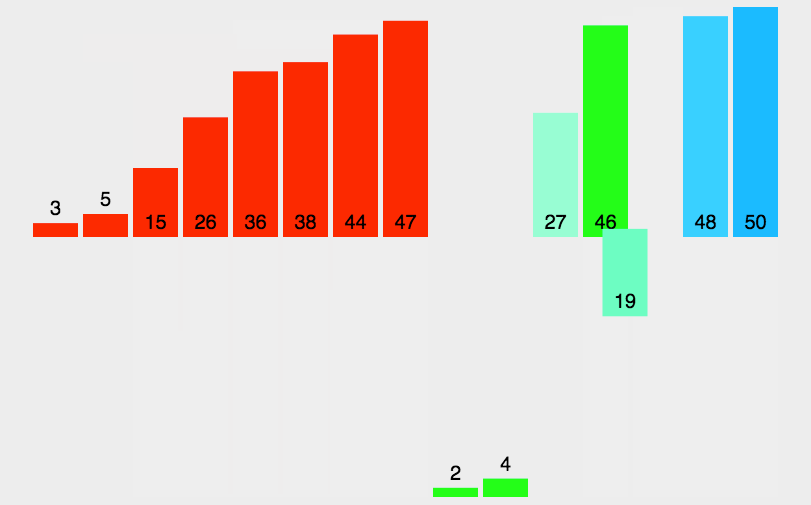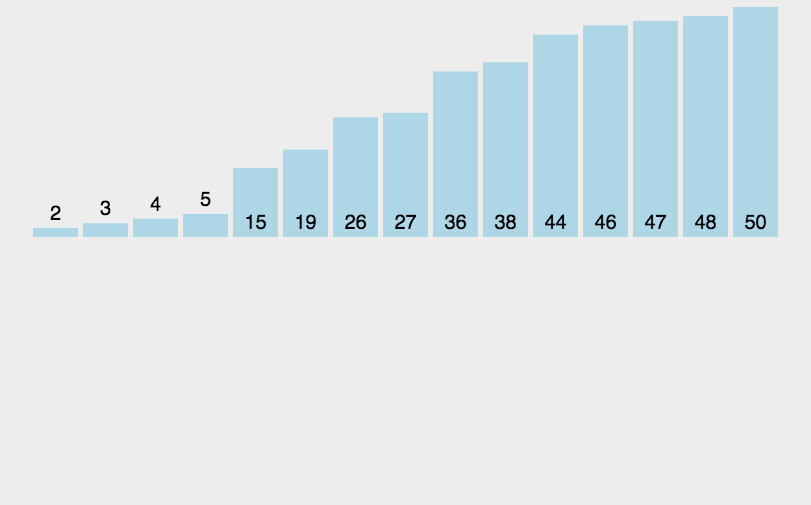
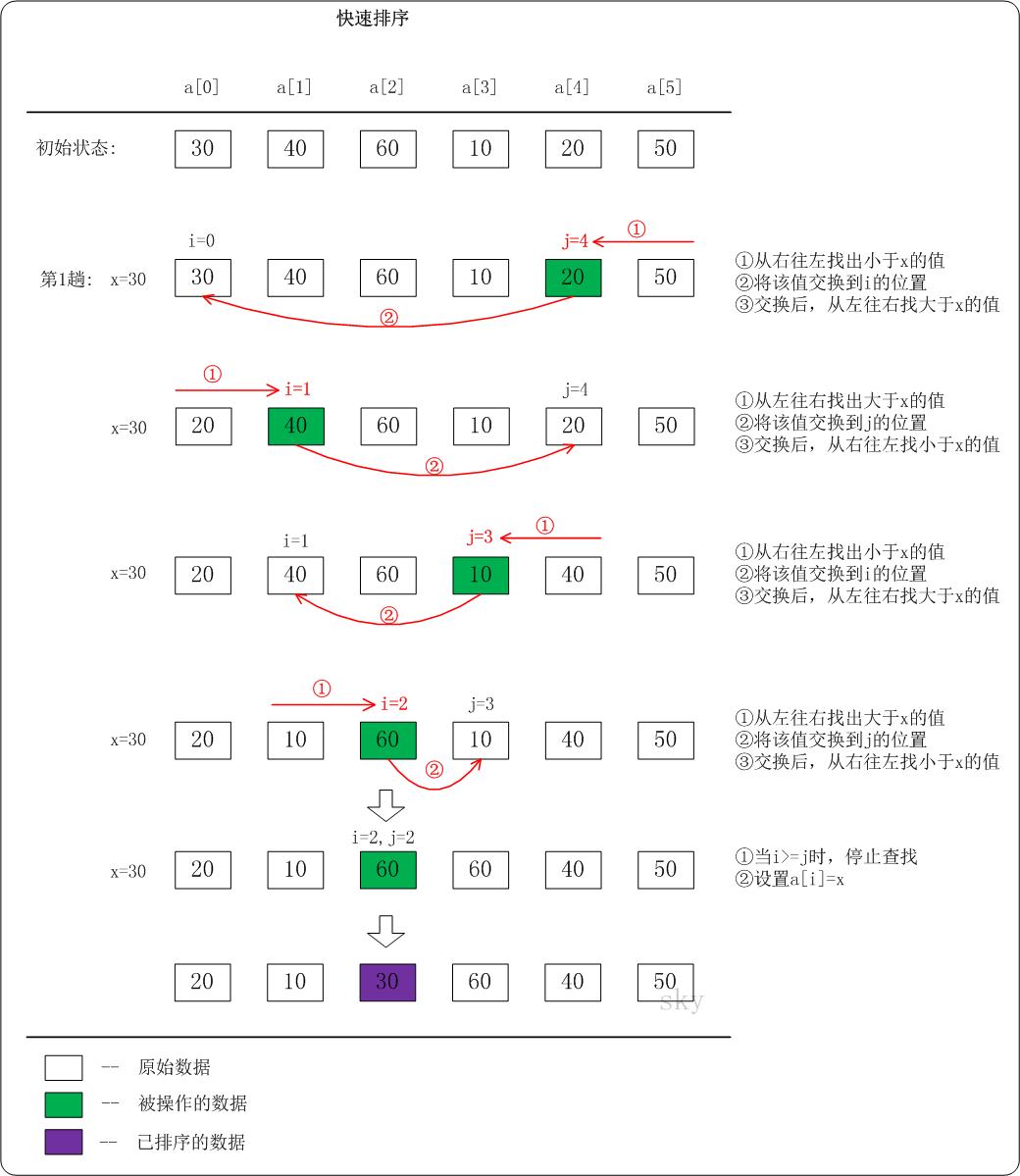
快速排序