常用损失函数和模型评价指标小结
一、损失函数/代价函数/误差函数
1.1 回归问题
平方损失函数(最小二乘法)
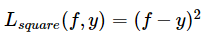
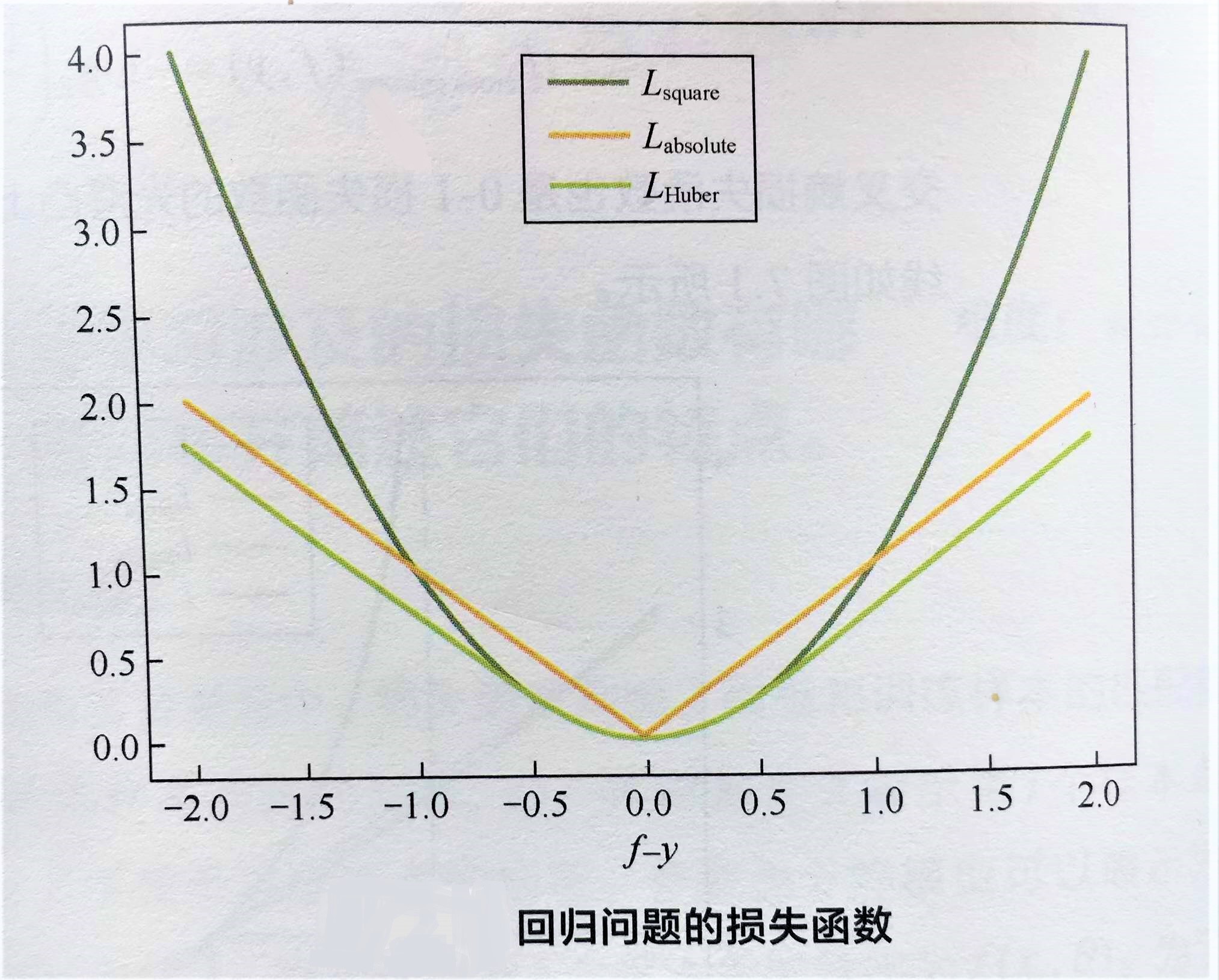
光滑损失函数,可用梯度下降法求最优解,
缺点:异常点该损失函数惩罚力度大,因此,对异常点比较敏感。为解决该问题,可以采用绝对损失函数
绝对损失函数
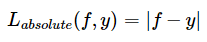
对异常点更鲁棒一些,
缺点:在f=y处无法求导。综合考虑可导性和对异常点鲁棒性,可采用Huber损失函数
Huber损失函数
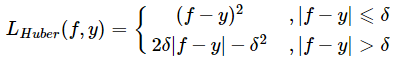
|f-y|较小时,为平方损失,在|f-y|较大时,为线性损失,就解决了异常点鲁棒问题。同时,分段函数处处可导。
缺点:但,Huber损失的问题是我们可能需要不断调整超参数delta。
1.2 分类问题
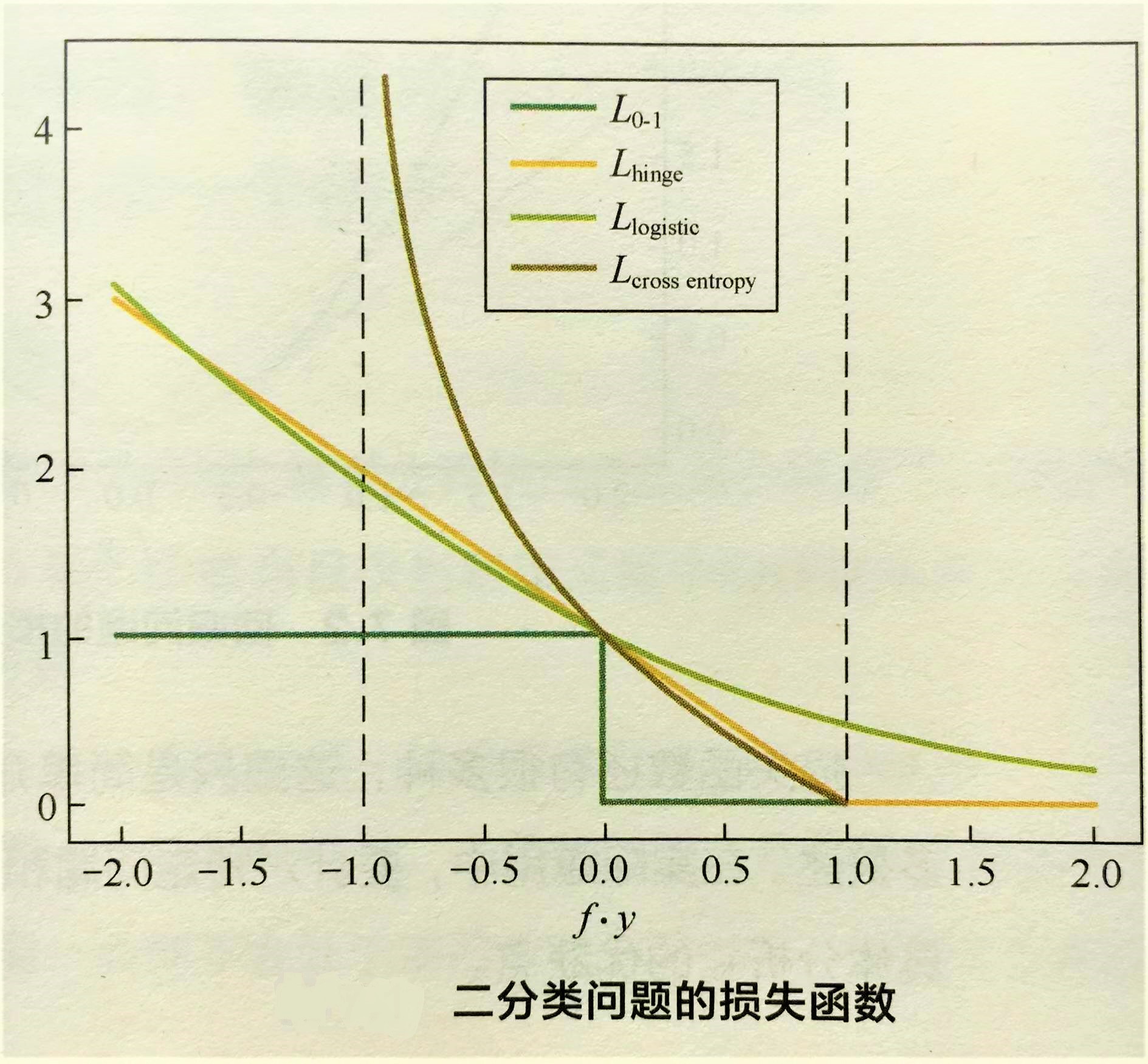
0-1损失函数
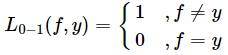
能直观刻画分类错误率,
缺点:由于非凸、非光滑,很难对该函数进行优化求解
应用:0-1损失函数在朴素贝叶斯模型的推导中会用到。
Hinge损失函数
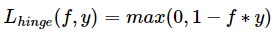
是0-1损失函数一个代理函数,且是它相对紧的凸上界;fy>1时,该损失函数不对样本点做任何惩罚,
缺点:在f*y=1处不可导,不能用梯度下降法求最优解,而是用次梯度下降法
应用:Hinge损失函数是SVM模型的基础
指数损失函数
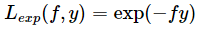
应用:指数损失函数在AdaBoost模型的推导中会用到。
对数损失函数
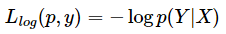
应用:对数损失函数在Logistic回归模型的推导中会用到。
Logistic损失函数
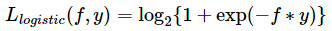
是0-1损失函数另一个代理函数,且是它的凸上界,且该函数处处光滑,可用梯度下降求解,
缺点:该损失函数对所有样本点有所惩罚,所以对异常值相对更敏感。
交叉熵(Cross Entropy )损失函数
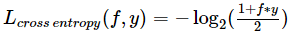
当预测值f属于[-1,1],是0-1损失函数另一个常用代理函数,且是它的光滑凸上界。
二、评价指标
2.1 回归问题
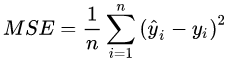
绝对误差(MAE)L1
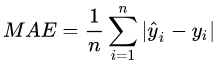
R-squared:决定系数,是一个评价拟合好坏的指标。被人们称为最好的衡量线性回归法的指标。
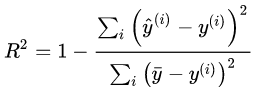
如果我们使用同一个算法模型,解决不同的问题,由于不同的数据集的量纲不同,MSE、RMSE等指标不能体现此模型针对不同问题所表现的优劣,也就无法判断模型更适合预测哪个问题。 得到的性能度量都在[0, 1]之间,可以判断此模型更适合预测哪个问题。
2.2 分类问题
混淆矩阵
准确率
查准率(响应率)
查全率(召回率/捕获率)
P-R曲线
ROC曲线
AUC值
KS值
2.3 聚类问题
外部指标
Jaccard(杰卡德)系数
FM指数
Rand指数
标准化互信息
内部指标
DB指数
Dunn指数
轮廓系数
定义:轮廓系数适用于训练样本类别信息未知的情况。假设某个样本点与它同类别的群内点的平均距离为a,与它距离最近的非同类别的群外点的平均距离为b,
则轮廓系数定义为
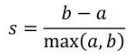
性质:
(1)轮廓系数的取值范围是[−1,1],同类别样本点的距离越近,且不同类别的样本点距离越远,则得到的轮廓系数的值就越大。
(2)对于一个样本集合,它的轮廓系数是所有样本轮廓系数的平均值。
【参考】
【2】机器学习模型评估指标汇总
轮廓系数适用于训练样本类别信息未知的情况。假设某个样本点与它同类别的群内点的平均距离为a,与它距离最近的非同类别的群外点的平均距离为b,则轮廓系数定义为



