数据标准化和归一化 方法小结
特征缩放主要几种方法：
| 类型 | 规范化方法 | sklearn 类名 | 说明 |
| 标准化 | Standardization 标准差标准化 | StandardScaler | 得到均值为0，标准差1的近似正态分布。如果存在异常值，标准化后影响程度也被降低。 |
| / | 稳健标准化 | RobustScaler | RobustScaler和StandardScaler比较近似，但是它并不是用均值和方差来进行转换，而是使用中位数和四分位矩。我个人比较喜欢将RobustScaler这种方法称为“粗暴缩放”，因为它会直接把一些异常值踢出去，有点类似我们看体育节目中评委常说的‘去掉一个最高分，去掉一个最低分’这样的情况。 |
| 区间化 | Min-max normalization 极差归一化 | MinMaxScaler | 移动并缩放数据，默认区间化到[0,1]，也可指定到其它任何区间。 |
| / | Scaling to unit length 缩放至单位长度 | Normalizer | 对每个样本点进行缩放，使得特征向量的欧式长度等于1。注意：这种是以样本（行）为单位，不是以特征（列）为单位 进行L1或L2范数变换计算。 |
-
背景——>为什么要标准化？
数据标准化处理是数据挖掘的一项基础工作，不同指标往往具有不同的量纲和量纲单位，这样的情况会影响到数据分析的结果误差，为了消除不同指标之间的量纲和取值范围差异的影响，需要进行数据标准化处理，以解决数据指标之间的可比性。
什么是消除指标的量纲？
一般情况下，我们所收集的数据是有单位的，比如收集到一份个人信息，其中包括人的身高和体重两个指标，身高有单位cm，体重有单位kg，这俩指标对应数据量级差别就很大，导致数据的分析结果可能由量级较大的指标值决定，而忽略了量级小的指标。所以消除量纲是有必要的，去除不同指标数据单位的不统一，使之全部变成没有单位的可比较的数据，便于之后的分析。消除指标的量纲就是消除它们的单位。
什么是量纲？
物理量按照其属性分为两类：
1.物理量的大小与度量所选用的单位有关，称为有量纲量
2.物理量的大小与度量所选的单位无关，称为无量纲量去量纲指的是去除数据单位之间的不统一，将数据统一变换为无单位(统一单位)的数据集。
标准化（standardization）和归一化（normalization）都属于特征缩放（feature scaling）的方法，可以统称为数据“规范化”。
-
标准化vs归一化vs中心化定义
（1）如，Z-score结果只是消除量纲单位影响，统一变成均值0，标准差1的分布（不一定正态），使得不同变量之间具有可比性，叫做标准化；
（2）如，min-max除了消除量纲，还将结果都映射到一定区间（默认[0~1]）内，归一化因此得名，归一化也属于标准化范畴。
（3）数据的中心化是指原数据减去其平均值后（即离差结果），原数据的坐标平移至中心点（0,0），该组数据的均值将变为0，因此，也被称为零均值化。
简单举例：譬如某小公司老板员工共5人，5人的工资,分别为12000、5000、8000、3000、4000元，这5个数据作为一个独立的数据集，平均值为6400元，每个人的工资依次减去平均水平6400，得到5600、-1400、1600、-3400、-2400，新的5个数据其平均值等于0，这个过程就是数据的中心化。
-
标准化和归一化联系和区别
联系
标准化和归一化本质上都是对数据的线性变换，对向量X按照比例压缩再进行平移。二者都不会改变原始数据排列顺序。
区别
1、归一化会严格的限定变换后数据的范围，如默认[0 ,1]区间；标准化变换后的数据没有严格区间范围，只是其均值是0 ，标准差为1 的分布。
2、以min-max归一化为例，缩放比例只和极限值有关，通常受异常值影响大；Z分数标准化分母是标准差，缩放比例受所有样本点影响。
-
数据规范化两个主要作用
（1）保障模型准确性。
消除量纲单位，减少方差大的特征的影响，使不同量纲的特征处于同一数值量级，指标之间具有可比性，适合进行综合对比评价，提高分类器的准确性；
一些算法需要计算样本点之间的距离(如欧氏距离)，例如KNN、kmeans等聚类算法。如果一个特征变量值域范围非常大，那么距离计算就主要取决于这个特征，出现“大数吃小数”的情况，从而与实际情况相悖。
（2）加快收敛速度。
在使用梯度下降的方法求解最优化问题时， 归一化/标准化后可以加快梯度下降的求解速度，即提升模型的收敛速度。对于线性模型，数据归一化使梯度下降过程更加平缓，更易正确的收敛到最优解。
（3）将数据限制到一定区间，使得运算更为便捷。
-
数据规范化2种方法（常用）
1，2方法都需要依赖样本所有数据，而3方法只依赖当前数据，可以动态使用，好理解。
1. Z-score标准化方法（标准差标准化 |0-1标准化）——>消除量纲影响，结果映射为均值为0，标准差为1的分布
转化函数为：
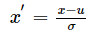，其中 μ为所有样本数据的均值（mean），σ为所有样本数据的标准差（standard deviation）。
性质：
（1）根据公式，新得到的标准化数据的意义是“给定数据距离均值相对来说有多少个标准差”。各个指标数据标准化之后数据就会全部统一起来，就不会有的指标数据非常大比如10000，而有的指标数据非常小比如10。
（2）如果原数据正态分布，经过标准化的数据就是标准正态分布，即均值为0，标准差为1。
（3）在Z-score标准化中，新的数据由于对方差进行了归一化，这时候每个维度的量纲其实已经等价了，每个维度都服从均值为0,、方差为1的正态分布，在计算距离的时候，每个维度都是去量纲化的，避免了不同量纲的选取对距离计算产生的巨大影响。
适用：
（1）适用于本身服从正态分布的数据。
（2）如果无从下手，可以优先考虑使用Z-score标准化，更通用，
（3）在后续算法计算中，涉及距离度量（KNN、聚类分析）或者协方差分析（PCA、LDA等）的，同时数据分布近似为正态分布，使用0均值化（Z-score）标准化表现更好（避免不同量纲对方差、协方差计算的影响）。因为Z-score标准化分母是标准差，该值综合了一个特征的所有值相对适中，按照标准差缩放更好保持了样本间距， 降低异常值影响。
（4）适用于特征变量最大值和最小值未知的情况。
2. min-max归一化（极差归一化）——>结果默认映射到[0,1]之间
转换函数如下：
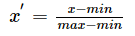
性质：其中max为样本数据的最大值，min为样本数据的最小值。是对原始数据的线性变换，使结果值映射到[0 – 1]之间。
适用：
（1）适用异常值较少，分布范围较稳定的数据。
（2）对处理后的数据区间范围有严格要求，eg：图像处理中，将RGB图像转换为灰度图像后将其值限定在 [0, 255] 的范围。
（3）或者不涉及距离度量、协方差计算。
缺点：
（1）这种方法有个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。
（2）另外，使用Max-Min标准化后，其协方差产生了倍数值地缩放，因此这种方式无法消除量纲对方差、协方差的影响，对PCA分析影响巨大.。因为当特征中有异常值时，由于min-max归一化分母是max-min，统一除以它，有可能将正常的数值“挤”到一起去，而标准化更好保持了样本间距。比如三个样本，某个特征的值为1,2,10000，假设10000这个值是异常值，用归一化的方法后，正常的1,2就会被“挤”到一起去。如果不幸的是1和2的分类标签还是相反的，那么，当我们用梯度下降来做分类模型训练时，模型会需要更长的时间收敛，因为将样本分开需要更大的努力！而标准化在这方面就做得很好，至少它不会将样本“挤到一起”。
延申：如果想要将数据映射到[-1,1]，则将公式换成：（X-Mean）/(Max-Min)。也可以根据（min-max归一化系数）*(b-a)+a 转换到任意 [a ,b] 区间。
补充：RobustScaler-稳健标准化（不常用）
转换函数：
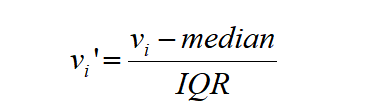，median是某特征中位数，IQR是四分位距；
处理方法：该缩放器删除中位数，并根据百分位数范围（默认值为IQR：四分位间距）缩放数据；
适用：当数据带有较多的离群值，推荐使用。RobustScaler和StandardScaler（标准差标准化）比较近似，但是它并不是用均值和方差来进行转换，而是使用中位数和四分位矩。
-
其它非线性变换
3. Z-scores 简单化——>结果映射到[0,1]之间
模型如下：x = 1/(1+x)
性质：x越大证明x越小，这样就可以把很大的数规范在[0 ， 1]之间了。
应用：在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维、涉及到正态分布的时候使用该方法较好。
4. 三角函数——>结果映射到[0,1]之间
三角函数的值在[0, 1]之间，如果有需要，可以用三角函数进行变换。
5. sigmoid函数——>结果映射到[0,1]之间
sigmoid函数，也称S型函数，公示为：S(x) = 1/(1+e-1) 可将数据映射到[0 ，1]
作用：可以对数据进行有效的压缩。特别的，S型函数在逻辑回归中起着决定性作用。
6. 对数变换
对数规范化的常见形式是：-ln(x+1) ——>当x大于0时，结果映射到[0 ,+∞]
应用：在实际工程中，经常会有类似点击次数/浏览次数的特征，这类特征是长尾分布的，可以将其用对数函数进行压缩。特别的，在特征相除时，可以用对数压缩之后的特征相减得到。
7. 小数定标
小数定标主要是对单位的换算和进制的转换，使得数据得到一定的简化与压缩。
如通过移动小数点的位置来进行标准化，小数点移动多少位取决于属性A中取值的最大绝对值，计算方法x'=x/(10k)，k是满足条件的最小整数。假如A属性从-988~918 ,我们用1000（即k=3）除每个值，这样-988就被规范化为-0.988。
8.box-cox变换
boxcox变换主要是降低数据的偏度，通常回归模型残差非正态或异方差的时候，会选择对y做boxcox变换，降低y的偏度，让y更接近正态。
参考
【2】归一化（normalization）、标准化（standardization）以及正则化（regularization）比较
【3】数据为什么要标准化？
