数理统计要点

虽然我也粗读过统计学的几本书，但从易懂性来说，都没有学校老师给的ppt好，或者说自己看书比较困难，但是听老师讲课就很容易懂。所以，我建议有条件的同学能够选修统计学这门课，没条件的同学可以去网上找一些相关视频，配套书籍可以选择茆诗松的《概率论与数理统计》。另外，《Head First Statistics》一书可以用来预热。

统计学有个形象的顺口溜。学了统计学，你至少应该知道：

初级说一说 ——> 描述性统计

中级比一比 ——> 推断性统计 /差异性分析

高级找关系 ——> 统计模型

一、概率论

　　互斥事件、对立事件、独立事件：

　　　　互斥事件为同一样本空间中，A、Ｂ事件无交集，只要Ａ发生了，Ｂ就不可能发生，但Ａ发生了，Ｂ不一定发生（有可能是Ｃ、Ｄ……其它事件发生）；

　　　　对立事件为样本空间中仅有A、B两个可能事件，非A即B；

　　　　独立事件，Ａ、Ｂ分处不同样本空间，互不影响。

　　古典概型

　　　　随机事件仅包含有限个事件，且每个事件出现的可能性相同

　　先验概率、后验概率

　　　　由以往数据分析得到的概率叫先验概率；得到最新信息后，再重新加以修正的概率叫后验概率

　　全概率公式

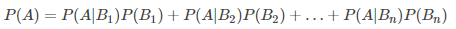
　　贝叶斯公式

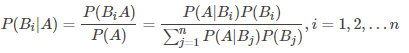
　　有放回的抽样（独立重复抽样）

二项分布：n次0-1分布重复试验，某事件发生k次的概率。公式：B(n,p)=P(X=k)=(n,k)pk(1-p)n-k，k=0,1,2,…；

　　负二项分布（帕斯卡分布）：n次0-1分布重复试验，直到某事件发生k次的概率（即：最后1次一定发生，前n-1次发生k-1次即可），为二项分布的变体。公式：P(X=k)=(n-1,k-1)pk(1-p)n-k

　　几何分布：n次0-1分布重复试验，某事件直到第k次首次发生的概率（即：前k-1次一定都不发生，只有一种可能性）。公式 G(p) =p(1-p)k-1,k=1,2,…，它的一个重要性质是无记忆性。

　　不放回抽样

　　超几何分布：在不放回抽样中，利用排列组合精确计算，事实上当N很大时，可近似二项分布计算。如：共有N个球，其中红球个数为D，其余为白球，从中抽n个球出来，求抽中k个红球的概率，即为超几何分布问题，其公式为：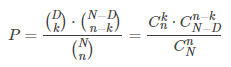　

二、描述性统计

　　2.1 统计量

　　　　描述水平（集中）的统计量

　　　　　　均值、中位数、分位数、四分位间距（IQR）、众数...

　　　　描述差异（离散）的统计量

　　　　　　极差、离差、方差、标准差（均方根差）、变异系数（COV）、协方差（Cov）、皮尔逊相关系数、均方误差（MSE）、均方根误差（RMSE）...

　　　　描述分布形状的统计量

　　　　　　偏度、峰度

　　2.1 常用概率分布及应用

　　　　离散型

　　　　　　0-1分布、二项分布、几何分布、超几何分布（注：不放回抽样）、泊松分布

　　　　连续性

　　　　　　均匀分布、指数分布、正态分布（高斯分布）、卡方分布、t分布、F分布

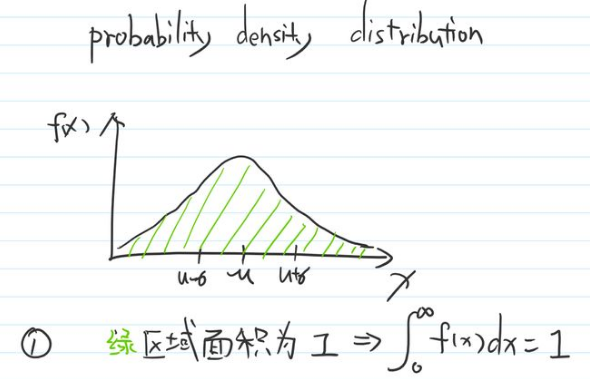
正态分布——>是自然界最常见的一种分布，对应的分布函数f(x)是连续型的概率密度函数。表征的是某一事件的发生概率，可以形象的认为X轴就是该事件中的各种情况，而Y轴对应的是这种情况发生的概率，因此曲线与x轴的合围面积意义就是某个事件各种可能的概率之和一定是1，数学表示为概率密度f(x) 积分面积为1（其实任何连续概率密度函数全域（-∞，+∞）积分后结果都是1，这是由它的意义决定的）。

正态分布由两个参数——平均值μ和方差σ^²决定，μ确定了正态分布图的平分线，σ确定了钟型宽窄，它和其它各种分布都有着直接或间接的联系。比如说二项分布，其实每个人抽取n次，最后的结果都是不尽相同的，这是由于抽样误差引起的。但是，如果好多人（N）都做这么一次试验（每个人都抽n次，并记录下正品数），那么这N个人抽到的正品数的分布就是一个正态分布了。

正态分布经过 Z-score =(x-μ)/σ 标准化后，就变成了μ=0，σ=1的标准正态分布。 Z-score几何意义是自变量与平分线的距离是几个标准差。

　　特别容易理解错误的概念：虽然积分的几何意义是面积，但算法是两个曲线分别与x轴的合围面积之差，即I =∫ [ f(x) -t(x)] d_x。而不是曲线沿x轴线区间分割为n个长方形Δx*Δy，再将每个长方形面积加起来。因此这样就不难理解为什么正态分布的概率密度函数积分后<=1了。其实是I =∫ [ f(x) -0] d_x

卡方分布——>设 X1..Xn是服从标准正态分布的随机变量，则称统计量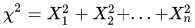服从自由度为n的卡方分布（标准正态分布随机变量的平方和），记为 $\chi ^{2} \sim \chi ^{2}(v)$ ，其中v称为自由度。卡方分布期望和方差： $E(\chi ^{2}) = v$ ， $D(\chi ^{2}) = 2v$ 。

t分布——>用于根据小样本来估计呈正态分布且方差未知的总体的平均值。如果总体方差已知，则应该使用正态分布。

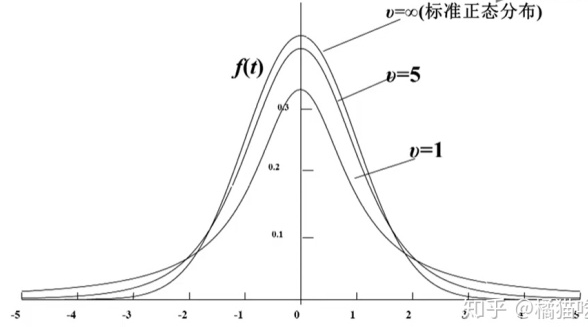
t分布曲线的特点：

t分布曲线是单峰分布，它以0为中心，左右对称。
t分布的形状与样本数n有关。自由度ν越小，t值越分散，曲线的峰部越矮。自由度v越大，t分布越逼近标准正态分布。
t分布不是一条曲线，而是很多曲线的集合（一簇曲线）。

三、推断性统计

——>以小推大，以微观推宏观，以样本推总体

3.1 样本与总体分布的关系&检验统计量

　　　　样本与总体分布的关系（理论依据）

大数定理 ——>就是当样本容量独立随机且足够大的时候，样本均值就约等于总体均值。

中心极限定理 ——>无论原本的总体是什么鬼分布，通通不管。随着实验抽样次数增多，每一次只要抓出来的样本足够，样本均值的抽样分布趋向于服从正态分布。这里需要特别注意的是，抽样次数并不是样本量，一次实验只是一次抽样，只能得到一个样本均值。而n次抽样会得到n个值，这些值的分布才是正态分布。

检验统计量（非常重要）

Z 检验（常用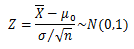）——>又叫Z-分数（此处分母之所以标准差是σ/√n，因为算的是样本均值的标准化），其实就是正态分布中的标准正态变量。因此，Z检验可以简单理解为标准化检验。而在给定显著性水平α后，从临界值表中，查询置信度1-α对应的临界值就是基于标准正态分布的唯一对应关系，然后临界值又能通过Z检验统计公式反推出置信区间。因此，它起到了一个很重要标准化中转的作用。既可以用作区间估计的枢轴量，也可以用作假设检验中的检验统计量。

卡方检验——>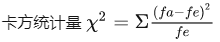，，其中fa表示观察值频数（实际观测值），fe表示期望值频数（理论推断值）

卡方检验的根本思想就是比较实际观测值和理论推断值的吻合程度或者拟合优度问题。卡方值越大，二者偏离程度越大；如果两个值完全相同则卡方值为0。卡方检验是非参数检验，适用于布尔型数据和二项分布数据。

主要用于（1）拟合优度检验（检验一组给定的数据与指定分布的吻合程度），（2）独立性检验（检验两个变量的关联性）。

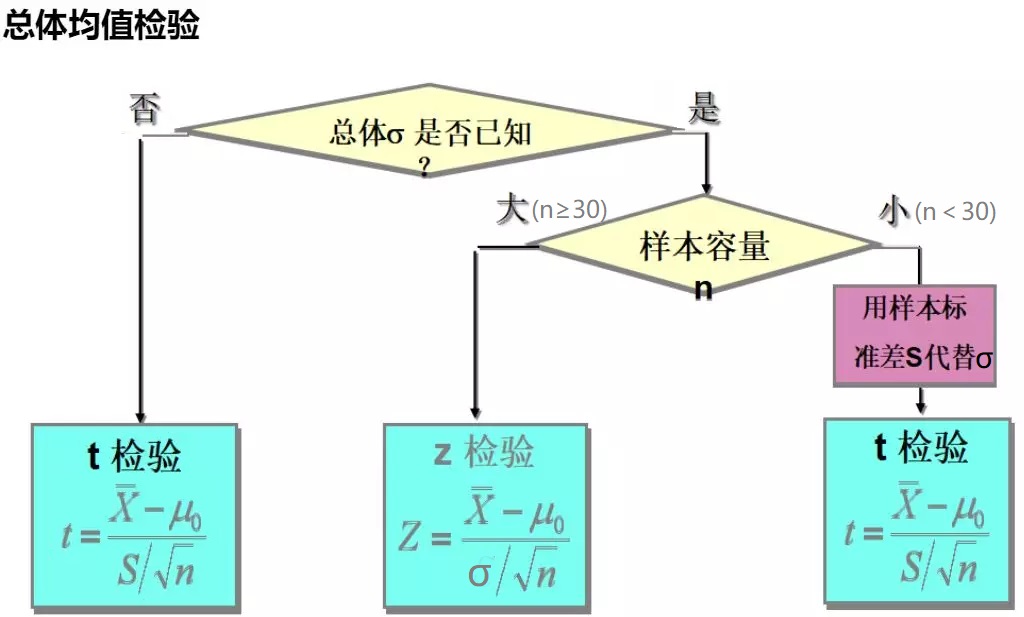
　　t 检验（常用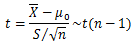）——>，这家伙的图形与正态分布根本看不出太大区别，主要用于假设检验的均值检验（特别是小样本和未知总体方差的检验）。对于大于120的样本，t检验和正态的Z检验等效。用于对小批量样本时，使用样本方差代替总体方差的统计量只要把Z统计量中的σ换成S就可以了，不过注意的是查的表是不一样的，t检验查的是t分数表，查的是自由度（样本量）和概率（置信度）、分数（临界值）三者的关系！

F 检验——>主要用于假设检验中的方差齐性检验。比较两个样本的方差是否齐性，以及单/多因素试验中的方差分析。

　　3.2 参数估计

　　　　点估计——>是估计参数一个确定的值。

　　　　　　矩估计法

　　　　　　最大似然估计法

区间估计——>估计参数的范围。估计这个参数有多大的概率（即置信度或叫置信水平：1-α。为何是1-α而不是α，这是约定俗成的问题，在假设检验的时候，α就叫作显著性水平，那么置信水平就是1-显著水平了）落在某个区间范围，即置信区间（置信下限，置信上限）。

显著性水平：符号α，表达了区间估计的不可靠性，如α=0.05，是说总体指标在置信区间内平均100次只有5次会产生错误。

置信度：又叫置信水平1-α，则表达了区间估计的可靠性；

临界值：其实是原假设样本均值通过枢轴量（Z、t）标准化转换后的一个标准量。就类似于正态分布标准化；

置信区间：表达了区间估计的精确度；

转换关系：

人为主观指定了【显著性水平α】，就等于明确了【置信度1-α】，再根据置信度与枢轴量函数Z的分布关系，即置信度 =∫f(z)dz=∫_a^bg(u)du，就能得到样本对应总体的【置信区间】，置信区间通过枢轴量函数（Z、t等）标准化后的值其实就是【临界值】。而p-值是直接将样本均值经过枢轴量标准化后再向一端或两端积分的小概率结果，这样就可以直接与给定的显著性水平比较，从而做假设检验判断。

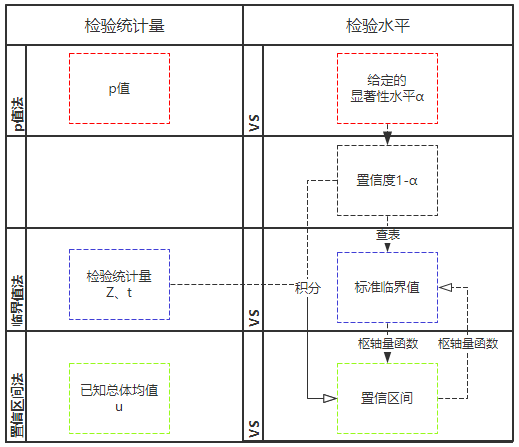
计算步骤

1、判断是否正态总体，人为设定置信水平1−α；

2、找到枢轴量，在假设检验中叫检验统计量（简单的说，就是一个关于随机变量X及参数μ的函数。它有自己单独的、与变量及参数都无关的标准分布，这样就可以用置信水平和这个分布特征来确定函数内的参数μ的置信区间）；

3、利用枢轴量函数的分布求出置信水平1−α对应的置信区间，即根据枢轴量函数计算出μ $θ$

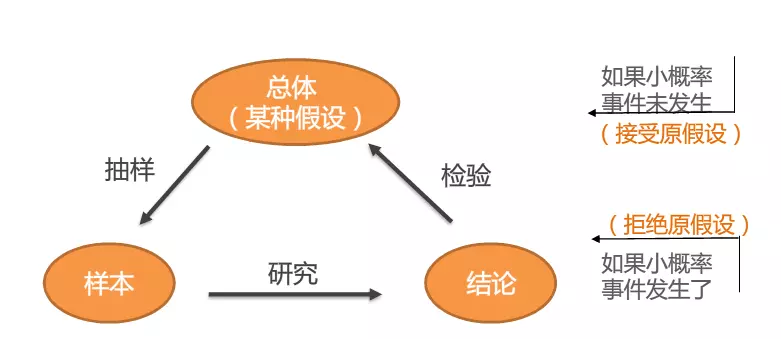
3.3 假设检验——>假设检验与参数估计其实是一样意思，区别就是多做两步工作（开始先假设+最后再判断）

　　假设检验本质，是验证抽样的样本计算特征（p值、检验统计量等）是否满足中心极限定理正态分布下的理论结果。而计算特征又由样本值和样本量n决定，因此，我们还可以通过给定的检验水平（显著性水平或临界值），知道满足假设检验的最低样本量n应该是多少。

　　基本思路：小概率反证法思想。小概率思想认为小概率事件在一次试验中基本上不可能发生。在这个方法下，我们首先对总体作出一个通常会成立的原假设H0（它的反面就是备择假设H1），按照这个原假设进行下去，根据中心极限定理（只要样本足够多，理论会符合正态分布），样本计算得到的检验统计量（p值或Z/t等统计量）正常会>人为给定的检验水平（显著性水平α或临界值）。然后想办法证明得到的检验统计量< 人为指定的显著水平，即原假设下的小概率极端事件发生了，以此来证明原假设错的很“显著”，来拒绝原假设。检验水平其实是基于标准正态分布下给的一个标准参照系。

　　比如：原假设两个总体没有显著性差异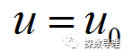，备择假设两个总体有显著差异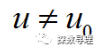。之后我们可则以构造一个与此相关的描述两个样本差异尺度的检验统计量F，如果该统计量F非常的大（即已经超过了一定的临界值F( α)），那么试验结果和原假设相背离，我们则可以认为这种差异并不仅仅是由抽样误差带来的，就有理由怀疑原假设的真实性，因此我们可以拒绝原假设，认为两个总体有显著差异。

　　进一步来看，除了通过计算检验统计量是否超过临界值进行判断之外，还可以计算P值。P值的含义是，当原假设为真的情况下，根据样本所计算得到的检验统计量F极端小概率事件发生的概率。因此可知，当P值小于 640?wx_fmt=png ，则检验统计量F大于临界值F( α)，我们可以拒绝原假设；当P值大于，则检验统计量F小于临界值F( α)，我们不能拒绝原假设。特别地，如果我们的检验统计量F恰好等于临界值F( α)，则我们的P值将恰好等于。

　　在这里，小概率事件的阈值 640?wx_fmt=png ，我们称之为检验水平，一般情况下我们取，即把发生概率小于0.05的事件称之为小概率事件。相反，如果我们假设检验中，没有拒绝原假设，并不意味着我们完全接受原假设，只是说明样本数据的“证据”不足，暂时不拒绝原假设。

　　　　检验统计量函数选择：

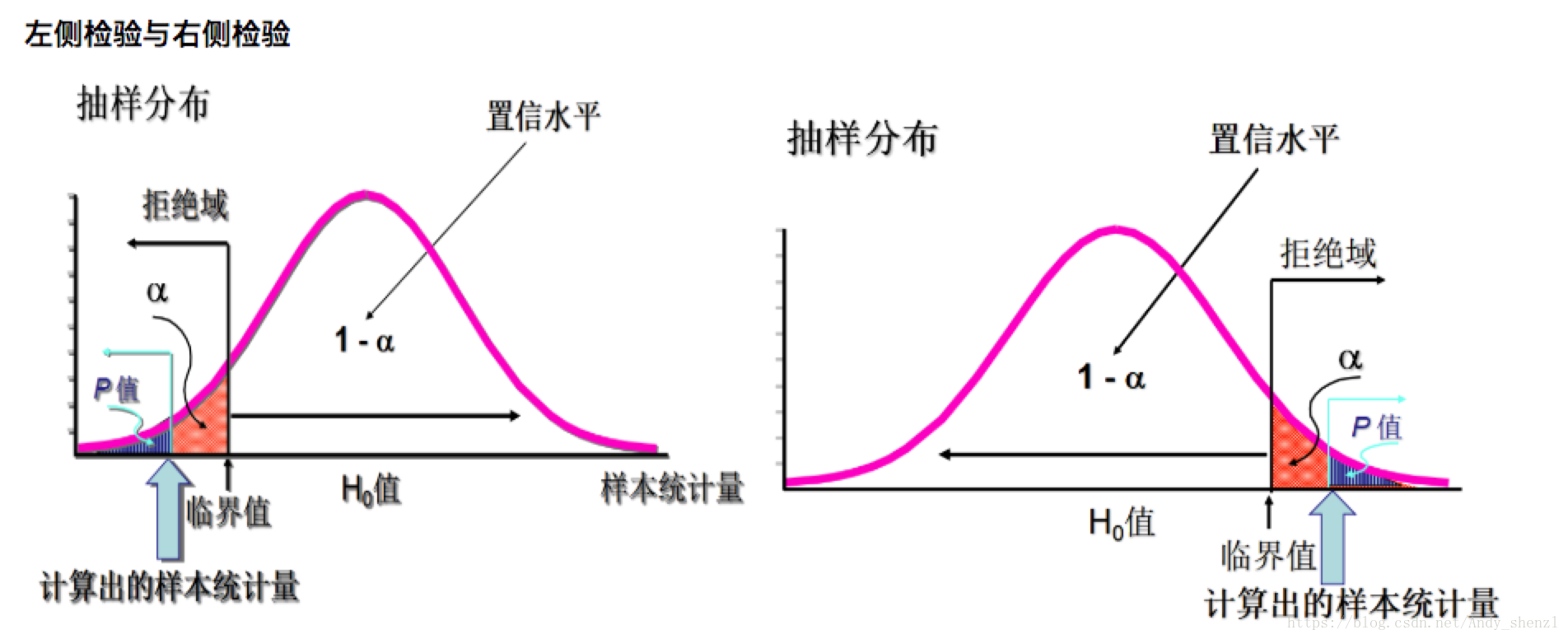
　　　　单双侧检验确定：

　　　　　　原假设H0：u=u₀（u>=u0），备择假设H1：u<u₀（——>左检验）

　　　　　　原假设H0：u=u₀（u<=u0），备择假设H1：u>u₀（——>右检验）

　　　　　　原假设H0：u=u₀ ，备择假设H1：u≠u₀（——>双边检验）

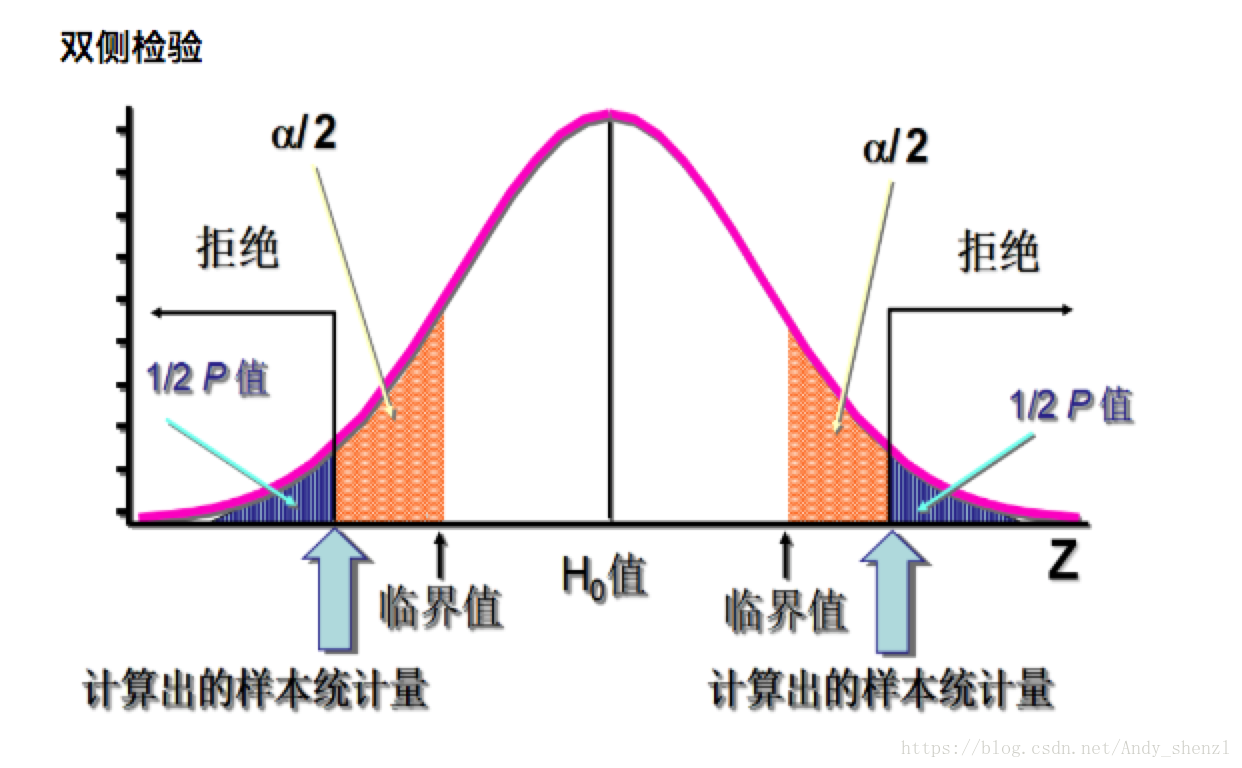
　　　　计算步骤：

　　　　　　1、对样本总体关系提出假设，原假设H0和备择假设H1（一般将研究者支持的需要验证的结论作为备择假设H1，其反面欲证明不正确的作为原假设）；

　　　　　　2、选择合适的假设检验方法，设定检验水平（显著性水平α或临界值），计算原假设检验统计量（Z检验、t、卡方、F等）；

　　　　　　3、比较假设检验统计量与检验水平大小，判断作出是否拒绝原假设结论。（也可理解为拒绝原假设犯错的概率是否小于给定的概率临界值。）　

（1）若原假设事件小于检验水平，即落在拒绝域，可以拒绝原假设，认为与原假设有显著性差异。

（2）若原假设事件大于检验水平，即落在接受域，不可拒绝原假设，认为和原假设没有显著性差异。（注意：这里不能拒绝原假设，只是样本“证据”不足，即没有足够的理由否定拒绝原假设，并不意味就接受原假设，两者不一样的。接受意味的是原假设一定成立。比如原假设是有只有1块钱在身上，不能拒绝原假设的意思是，我不知道你有没有1块钱在身上，你有可能没钱，有可能只有1块钱，也有可能有很多钱，而接受原假设的意思是，你只有1块钱，这个要非常注意，不能乱作判断！））

　　　　特别注意：

（1）统计上的显著性和实际生活中的显著性是不一样的。

（2）显著性水平是个较为主观的标准，不是一个固定不变的值，依据拒绝区间可能承担的风险来定。

（3）假设检验方法选择要

　　　　P值法（常用）——>比较P值vs指定的显著性水平α

　　　　　　1、与临界值法的区别就是，基于假设前提下，代入计算检验统计量（假如为Z检验统计量），并进一步单侧或两侧积分求得P值（P-value）。

　　　　　　2、将P值大小与实验前人为指定的显著性水平α（阈值）进行比较，若P值小于α，则为显著拒绝原假设。另外，P值也代表着拒绝原假设的最小显著水平。

　　　　临界值法——>比较检验统计量vs指定的临界值

1、与置信区间法的区别就是，置信区间法是比较总体均值μ0 是否落在样本均值X¯的置信区间（假设为Z检验统计量），而临界值法则是，基于假设前提下，将总体均值、标准差、样本均值等代入检验统计量中计算，即。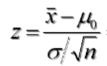

2、再对比检验统计量结果Z与临界值Z_α（实验前人为指定的显著性水平α查表得到）大小，若结果落在临界值Zα以外（即落在拒绝域，则表示原假设H0下的小概率事件发生了），则拒绝原假设，接受备择假设；否则，不能拒绝原假设。

　　　　置信区间法——>比较假设的样本总体均值是否落在指定置信度对应的置信区间

　　　　　　1、判断是否正态总体，建立假设（原假设H0：总体均值=u0）

　　　　　　2、找到检验统计量(在区间估计中叫枢轴量)，利用检验统计量的分布求出人为指定的置信水平1-α的置信区间；

　　　　　　3、比较假设的样本总体均值u0是否落在置信区间，若落置信区间以外，则可以拒绝原假设；若落在置信区间之内，则不能拒绝原假设。

　　　　假设检验小结：

　　1、不管用哪种检验方法，只要把比较维度转换到和给定的检验水平一致即可。

　　2、区别：显著性检验主要是看显著水平下计算得到的检验水平与实际检验统计量值的比较，而置信区间是根据显著水平得到的样本总体均值估计区间与原假设总体均值比较。例如，在比较一个样本总体均值是否为0时，就看0是否落在了置信区间，若是，则不显著，否则是显著的。

四、统计模型

　　4.1 简单方差分析

　　4.2 简单回归分析

　　4.3 ABtest

　　　　知乎 ABtest的统计原理和效果解读

五、重难点>>

基本的抽样方法
- 随机抽样
- 分层抽样
- 整体抽样
- 系统抽样

数据分布的描述统计量有哪些？一组样本数据分布的数值特征可以从三个方面进行描述：
- 描述水平（集中）的统计量：
  - 数据的水平：也称为集中趋势或位置度量，反应全部数据的数值大小。
  - 均值、
  - 中位数：与均值相比，中位数对极值并不敏感，因此，它通常更能代表偏斜数据的中心点。
  - 分位数
  - 四分位间距(IQR)： IQR=上四分位数-下四分位数=Q3-Q1。常应用：由最小值、下四分位数、中位数、上四分位数、最大值五个数可以画出箱线图，同时，通常以双侧大于1.5IQR作为异常值的判断，去掉异常值之后，再做箱线图，称为修正箱线图。
  - 众数
- 描述差异（离散）的统计量
  - 数据的差异：反应数据间的离散程度。
  - 极差：X_max－X_min 来评价一组数据的离散度。
  - 离差 Devition：计算方式——>单项数值x-均值μ_x，正负可以作为方向。用来反映某一数值与平均值的偏离程度（距离）。通常呢，离差都是用来进一步求标准差和方差的。
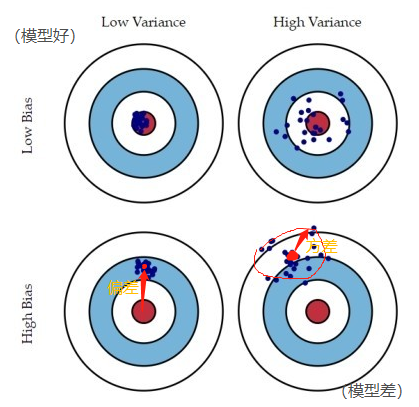
  - 方差Variance：度量变量和其数学期望（即均值）之间的离散程度。计算方式——>各个数据分别与其平均数之差的平方的和的平均数 D(X)=E{ [X−E(X)]²}。在机器学习中反映的是不同模型每一次输出结果与模型输出期望（平均值）之间的差异，即模型的稳定性，数据是否集中。刻画了同样大小训练集D_k变化对学习性能的干扰影响。Var=∑[f^{^}(x:D_k)-f^‾(x)]²/k
  - 残差 Residual：模型经过k伦迭代后，预测值与实际目标值的差，即 f^(x:D_k) -y。进一步残差可获得均方误差MSE、平均绝对误差MAE等，用作回归问题的损失函数。
  - 偏差 Bias：计算方式——>预测结果的均值与实际目标值的差值 Bias = f^‾(x) -y。“偏差” 跟 “平均值” 紧密联系在一起。反映了某种学习模型的平均估计结果所能逼近学习目标的程度，即模型本身的精确度。刻画了算法本身拟合能力。
  - 误差 Error：Error = 偏差Bias + 方差Variance + 噪声（刻画了学习问题本身难度，决定了预测好坏上限），此处应该叫模型泛化误差，与均方误差不同。均方误差类似对残差平方和的期望。

- - 标准差（又叫均方根差）：为了让方差结果更符合我们的直观思维，改进为标准差。计算方式——>方差开根号。
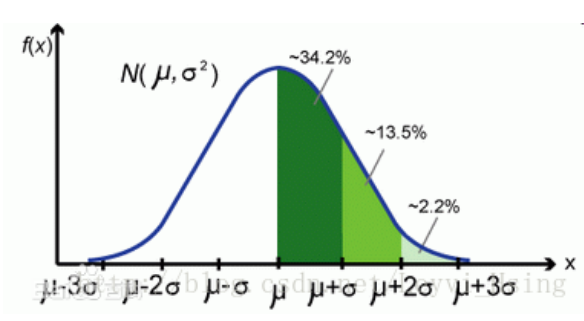
  - 举个例子：一个班级里有60个学生，成绩服从正态分布，平均成绩是70分，标准差是9，方差是81，那么我们通过方差不能直观的确定班级学生与均值到底偏离了多少分，通过标准差我们就很直观的得到学生成绩分布在[61,79]范围。（μ-σ，μ+σ）的概率为0.6826，即约等于下图中的34.2%*2。

- - 变异系数（Coefficient of Variation，COV）：又称为”离散系数“，计算方法——>c =标准差 δ/均值μ，这里的系数是在标准差基础上进一步消除量纲影响用来衡量一组数据自身离散程度的比例结果，是概率分布离散程度（相对变异性）的一个归一化度量。正是基于这个优点，实际应用中通常可用来比较均值显著不同的两组数据的离散程度，如果两组数据的测量尺度相差太大，或者数据量纲的不同，直接使用标准差来进行比较就不合适了，此时就应当消除测量尺度和量纲的影响。进行数据分析时，若变异系数大于15%，则考虑该数据可能不正常，应该剔除。
  - 协方差（Covariance，Cov）：计算方法——>Cov(X,Y) =E[X-E(X)]E[Y-E(Y)] = E(XY)-E(X)E(Y)，用于衡量两个变量的总体误差。虽然协方差能反映两个随机变量是否相关（协方差大于0的时候表示两者正相关，小于0的时候表示两者负相关），但是协方差值的大小并不能很好地度量两个随机变量的关联程度，一般会进一步用来算相关系数。
  - 皮尔逊相关系数：计算方法——>r(X,Y） =Cov(X,Y)/δxδ_y，研究两个变量之间相关程度，内涵本质是两个向量夹角的余弦值cosθ =a·b /|a|·|b|，因此-1 ≤r(X,Y) ≤1。性质：r=±1，线性相关；r=0，不相关；r介于0~1之间，正相关；r介于-1~0之间，负相关。
  - MSE （Mean Squared Error）均方误差：变量预测点同真实点之差的、平方的、期望。即残差平方和的期望，形式上有点像方差。MSE= ∑[f^{^}(x:D_k)-y]²/k。MSE 通常用作回归问题的损失函数。
  - RMSE（Root Mean Squard Error）均方根误差：标准差（均方根差）是变量数据与其均值的离散关系，通常用来衡量一组数自身的离散程度。而均方根误差是变量数据与真实值之间的偏差关系，用来衡量变量预测值同真实值之间的偏差。它们的计算过程类似，但是研究对象和研究目的不同。
  - RMS（Root Mean Squard）均方根值：计算方法——>变量数据先平方、再平均、然后开方，
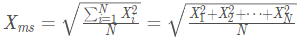
    即当真值为0时的均方根误差。在物理学中，常用均方根值来分析噪声。
  - 四分位差
  - 标准分数
  - MAE(平均绝对误差)：预测点与真实点之差的、绝对值的、平均值。MSE= ∑ |f^{^}(x:D_k)-y| /k
  - R-squared（确定系数 /拟合优度）：拟合优度是反映线性回归对观测值的拟合程度。那么度量拟合优度的统计量就是可决系数（亦称确定系数）R^2。R^2的取值范围是[0，1]。R^2的值越接近1，说明拟合程度越好。
  - 均值标准误(SE Mean)：度量样本均值多大精确程度地估计总体均值，并用于创建总体均值的置信区间。它等于样本标准差 (s) 除以样本数量 (n) 的平方根。
- 描述分布形状的统计量
  - 分布的形状：反应数据分布的偏度和峰度。
  - 偏度、峰度

了解重要的描述性分布，比如正态分布、chi-square分布、t分布、F分布等。

推断统计的假设检验是用来做什么的？置信区间的概念
- 假设检验和区间（参数）估计联系：
  - 二者都属于统计推断——利用样本数据统计量（statistic），对总体统计量（参数 parameter）的论断。都是以抽样分布为理论依据，建立在概率基础上的论断。论断结果有一定的可信程度或风险。
  - 对于同一统计量（问题参数）进行推断，二者使用同一样本、统计量、分布，因而区间估计问题和假设检验问题是可以相互转换的。区间估计中的置信区间对应于假设检验中的接受区域，置信区间以外的区域就是假设检验中的拒绝域。
- 区别：
  - 区间估计是根据样本统计量，来估计总体统计量（参数）；
  - 假设检验是根据样本统计量来验证总体统计量的先验统计量（参数）是否成立靠谱。
- 假设检验用来做什么？
- 为了从“不确定性”的角度来刻画两个变量的关系，就产生了假设检验，它解决的问题是“在多大程度上，某量A会等于B”，其中的“等于”可以换成“大于”“小于”等等。因为两个常量之间的相等关系是绝对的，你可以绝对地区分“A等于B”。但是，当在两个变量之间的话，就不存在“A等于B，或A不等于B”这种说法了。取而代之，可以用如下的说法“A有90%的可能等于B”，或者“在100次抽样中，A等于B的情况会出现90次”。当限定“程度”时，又可以解决如下问题“在90%的水平上，A会等于B吗？"
  - 在如此的解释框架下，比如，回归得到系数的假设检验，通常就是检验“在某个概率水平上，某个参数A是否等于0”等等。
- 区间估计

怎样进行数据预处理

怎样整理和显示数据

了解各种图的作用和适用场景，常用图包括散点图、折线图、条形图、直方图、饼图、箱线图、雷达图等

参考

【1】总结非常好的概率论与数理统计知识点

【2】假设检验原理

【3】如何通俗的理解假设检验基本原理

【4】统计学知识系列：一篇搞懂假设检验

利用检验统计量的分布求出人为指定的置信水平1-α的置信区间

方差Variance：度量变量和其数学期望（即均值）之间的离散程度。计算方式——>各个数据分别与其平均数之差的平方的和的平均数 D(X)=E{ [X−E(X)]²}。在机器学习中反映的是不同模型每一次输出结果与模型输出期望（平均值）之间的差异，即模型的稳定性，数据是否集中。

误差 Error：Error = 偏差Bias + 方差Variance + 噪声（刻画了学习问题本身难度，决定了预测好坏上限），此处应该叫模型泛化误差，与均方误差不同。均方误差类似对残差平方和的期望。

检验两个变量的关联性

posted on 2019-11-02 19:44 数说张小桃阅读(1301) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

听见涛声_数说张小桃

导航

公告