区别 |峰度（Kurtosis）和偏度（Skewness）

 

• 峰度（Kurtosis）
  • 定义

峰度又称峰态系数，表征概率密度分布曲线在平均值处峰值高低的特征数，即是描述总体中所有取值分布形态陡缓程度的统计量。直观看来，峰度反映了峰部的尖度。这个统计量需要与正态分布（也叫常态分布）相比较。

• • 公式

定义上峰度是样本的标准四阶中心矩（standardized 4rd central moment)。

随机变量的峰度计算方法为随机变量的四阶中心矩与方差平方的比值。

具体计算公式为：

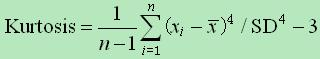
• • 性质　　　　　　

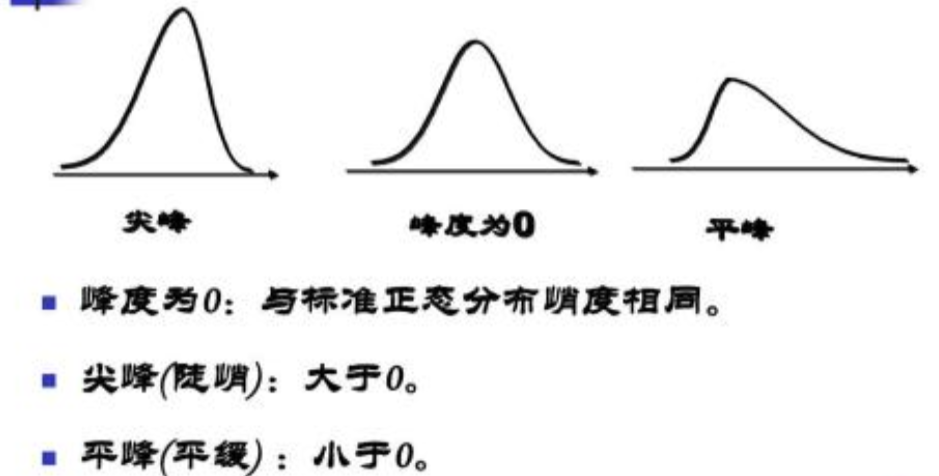
峰度 ≈ 0表示该总体数据分布与正态分布的陡缓程度相同；

峰度 >0表示该总体数据分布与正态分布相比较为陡峭，为尖顶峰；

峰度 <0表示该总体数据分布与正态分布相比较为平坦，为平顶峰。

峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。

 

 

• 偏度（Skewness）
  • 定义

偏度与峰度类似，它也是描述数据分布形态的统计量，其描述的是某总体取值分布的对称性的特征统计量。

• •  公式　　

定义上偏度是样本的标准三阶中心矩（standardized 3rd central moment)。

偏度的具体计算公式为：

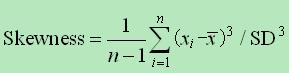
• •  性质　　

这个统计量同样需要与正态分布（也叫常态分布）相比较，

偏度 ≈ 0表示其数据分布形态与正态分布的偏斜程度相同；

偏度 >0表示其数据分布形态与正态分布相比为正偏（右偏），即有一条长尾巴拖在右边，数据右端有较多的极端值，数据均值右侧的离散程度强；

偏度 <0表示其数据分布形态与正态分布相比为负偏（左偏），即有一条长尾拖在左边，数据左端有较多的极端值，数据均值左侧的离散程度强

偏度的绝对值数值越大表示其分布形态的偏斜程度越大。

 

 

• •  理解中位数、众数、均值在偏态中的关系（记忆技巧）

技巧1：偏态说的是有一边的尾巴更厚，相当于某一边加了异常值。异常值对均值影响大，对中位数影响微小，对众数无影响，由此判断三者大小。

技巧2：不论正态还是偏态，都认为中位数两边样本量一样多。从正态到左偏，相当于中位数右侧的较大的数都集中到小的数上了，导致均值变小。同理右偏可以以相同的思路理解，均值变大。