Tensorflow笔记——神经网络优化过程

一、预备知识

tf.where() 

tf.where()  条件语句真返回A, 条件语句假返回B

tf.where(条件语句，真返回A, 假返回B)

a=tf.constant([1,2,3,1,1])
b=tf.constant([0,1,3,4,5])
c=tf.where(tf.greater(a,b), a, b)  # 若a>b, 返回a对应位置的元素，否则返回b对应位置的元素
print(c)  # tf.Tensor([1 2 3 4 5], shape=5,), dtype=32)

np.random.RandomState.rand()

返回一个[0,1]之间的随机数

np.random.RandomState.rand(维度)  # 维度为空返回标量

rdm=np.random.RandomState(seed=1)  # send=常数，每次生成随机数相同
a = rdm.rand()  # 返回一个随机标量
b=rdm.rand(2,3)  # 返回维度为2行3列随机数矩阵

np.vstack()

将两个数组按垂直方向叠加叠加

a=np.array([1,2,3])
b=np.array([4,5,6])
c=np.vstack((a,b)) 
# c: 
# [[1 2 3]
#  [4 5 6]]

np.mgrid[ ]   .ravel()  np.c_[ ]

np.mgrid[]   返回多维结构

　　np.mgrid[起始值: 结束值: 步长， 起始值: 结束值：步长，....]

x.ravel()  将x变为一维数组，将x拉直

np.c_[]  使返回的间隔数值点配对

　　np.c_[数值1， 数值2， ...]

 

 

二、复杂度学习率

复杂度

 学习率

可以先用较大的学习率，快速的到较优解，然后逐步减小学习率，使模型在训练后期稳定。

指数衰减学习率 = 初始学习率*学习率衰减率^(当前轮数/多少轮衰减一次)

 

三、激活函数

tf.nn.sigmoid(x) 

tf.math.tanh(x)

tf.nn.relu(x)  # 解决了梯度消失问题(在正区间)，收敛速度远快于sigmoid和tanh

tf.nn.leaky_relu(x)   

 四、损失函数

损失函数（loss）： 预测值（y）与已知答案（y_）的差距

NN优化目标：

　　loss最小

　　　　mse(Mean Squared Error)

         　  自定义

　　　　ce(Cross Entropy)

均方误差mse:

loss_mse = tf.reduce_mean(tf.square(y_-y)) 

五、欠拟合和过拟合

 

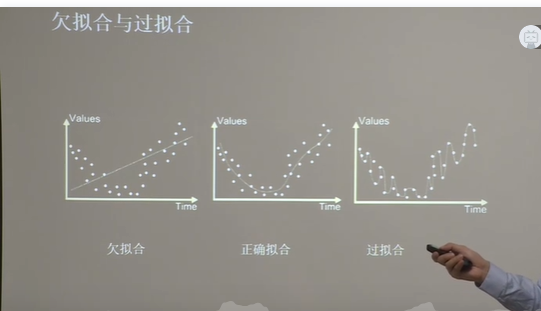
 欠拟合解决办法：

　　增加输入特征项

　　增加网络参数

　　减少正则化参数

过拟合解决办法

　　数据清洗

　　增大训练集

　　采用正则化

　　增大正则化参数

正则化在损失函数中引入模型复杂度指标，利用给w加权值，弱化了训练

数据的噪声（一般不正则化b）

六、神经网络参数优化器

待优化参数w, 损失函数loss, 学习率lr, 每次迭代一个batch, t表示当前batch迭代的总次数：