动态规划

一、简介

动态规划（dynamic programming）是通过组合子问题来求解原问题的方法，它应用于解决子问题重叠的情况，即不同子问题具有公共的子问题。

通常动态规划可以按照如下四个步骤进行设计：
1.刻画一个最优解的结构特征；
2.递归地定义最优解的值；
3.计算最优解的值，通常采用自底向上的方法；
4.利用计算出的信息构造一个最优解（按照要求，可有可无）。

首先什么样的问题适合用动态规划解决？

  • 符合“一个模型三个特征”的问题。
  • 那么问题又来了，什么是“一个模型，三个特征”？
  • “一个模型”👉：指 多阶段决策最优解模型；
  • “三个特征”👉：分别是最优子结构、无后效性和重复子问题。

二、”动态规划“的解题思路

  • 状态转移表法（回溯算法实现 - 定义状态 - 画递归树 - 找重复子问题 - 画状态转移表 - 根据递推关系填表 - 将填表过程翻译成代码）；
  • 状态转移方程法（找最优子结构 - 写状态转移方程 - 将状态转移方程翻译成代码）。

  • 动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。

三、练习题

1. 入门：

斐波那契数列，现在要求输入一个正整数 n ，请你输出斐波那契数列的第 n 项

# -*- coding:utf-8 -*-
class Solution:
    def Fibonacci(self, n):
        # write code here
        #斐波拉契数的边界条件： F(0)=0 和 F(1)=1
        if n < 2:
            return n
        else:
            a, b = 0, 1
            for i in range(n-1):
                a, b = b, a + b        #状态转移方程，每次滚动更新数组
 
            return b

2. 简单：

2.1 跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

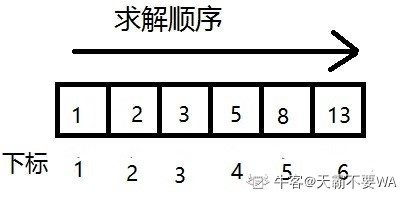
分析5阶台阶的答案，可以发现规律，总跳法数排列为斐波那契数列。

所以我们可以：

直接从子树求得答案。过程是从下往上。

我们可以通过推理来找出。
第3位可以由第1阶台阶跳2阶或第2阶段跳1阶段得出。
第4位可以由第2阶台阶跳2阶或第3阶段跳1阶段得出。
第5位可以由第3阶台阶跳2阶或第4阶段跳1阶段得出。

.....

最后可以得出：
dp[i]=dp[i-1]+dp[i-2];dp[i]=dp[i−1]+dp[i−2];

其中dp[i]表示跳到第i个台阶的走法

 

class Solution:
    def jumpFloor(self, number):
        # write code here
        dp = [0]*50
        dp[1] = 1
        dp[2] = 2
        for i in range(3,number+1):
            dp[i]=dp[i-1] +dp[i-2]
        return dp[number]

 时间复杂度：O(n) 空间复杂度：O(n) ###继续优化 发现计算f[5]的时候只用到了f[4]和f[3], 没有用到f[2]...f[0],所以保存f[2]..f[0]是浪费了空间。 只需要用3个变量即可。

class Solution:
    def jumpFloor(self, number):
        # write code here
        a,b,c =1,1,1
        for i in range(2,number+1):
            c = a+b
            a = b
            b = c
        return c

时间复杂度：O（n） 空间复杂度：O（1） 完美！

或者只用两个变量，c覆盖b

class Solution:
    def jumpFloor(self , number: int) -> int:
        # write code here
        a, b = 1, 1
        for i in range(number-1):
            a, b = b, a+b
        return b

2.2 最小花费爬楼梯

给定一个整数数组 cost \cost  ，其中 cost[i]\cost[i]  是从楼梯第i \i 个台阶向上爬需要支付的费用，下标从0开始。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。
 
数据范围：数组长度满足 1 \le n \le 10^5 \1≤n≤105  ，数组中的值满足 1 \le cost_i \le 10^4 \1≤costi​≤104 

示例1

输入： 
[2,5,20]
返回值： 
5
说明： 
你将从下标为1的台阶开始，支付5 ，向上爬两个台阶，到达楼梯顶部。总花费为5

示例2

输入： 
[1,100,1,1,1,90,1,1,80,1]
返回值： 
6
说明： 
你将从下标为 0 的台阶开始。
1.支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
2.支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
3.支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
4.支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
5.支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
6.支付 1 ，向上爬一个台阶，到达楼梯顶部。
总花费为 6 。
 题解：

动态规划, 每次走的步骤取决于前两个的状态; 状态转移方程: 当长度 < 2 时,直接返回 cost[0]; 当长度 >= 2 时,当前值取决于min(dp[i-1], dp[i-2]) + cost[i]; 代码如下:

class Solution:
    def minCostClimbingStairs(self , cost: List[int]) -> int:
        # write code here
        if len(cost)==1: return cost[0]
        n = len(cost)
        dp = [cost[0], cost[1]]  # 辅助数组
        for i in range(2,n):
            dp.append(min(dp[i-1], dp[i-2]) + cost[i])
        return min(dp[-1], dp[-2])

2.3 给定两个字符串str1和str2，输出两个字符串的最长公共子序列。如果最长公共子序列为空，则返回"-1"。目前给出的数据，仅仅会存在一个最长的公共子序列

数据范围：0 \le |str1|,|str2| \le 20000≤∣str1∣,∣str2∣≤2000
要求：空间复杂度 O(n^2)O(n2) ，时间复杂度 O(n^2)O(n2)

示例1

输入： 
"1A2C3D4B56","B1D23A456A"
返回值： 
"123456"

示例2

输入： 
"abc","def"
返回值： 
"-1"

示例3

输入： 
"abc","abc"
返回值： 
"abc"

分析：假设两个字符串s1,s2, 将两个字符串的第一个字符进行比较，分两种情况
1. 相等：比较s1,s2的第二个字符，此时最大的公共子序列长度为两个字符串之前的字符串最长子序列长度加一
2. 不相等
   1. 将s1的第二个字符s1[1]与s2第一个字符s2[0]进行比较
   2. 将s2的第二个字符s2[1]与s2第一个字符s1[0]进行比较
   此时两种情况的最大值为当前最大的公共子序列长度
由此构建状态转移表，以当前两个子字符串的公共子序列的长度为元素构建状态转移表如下：

 

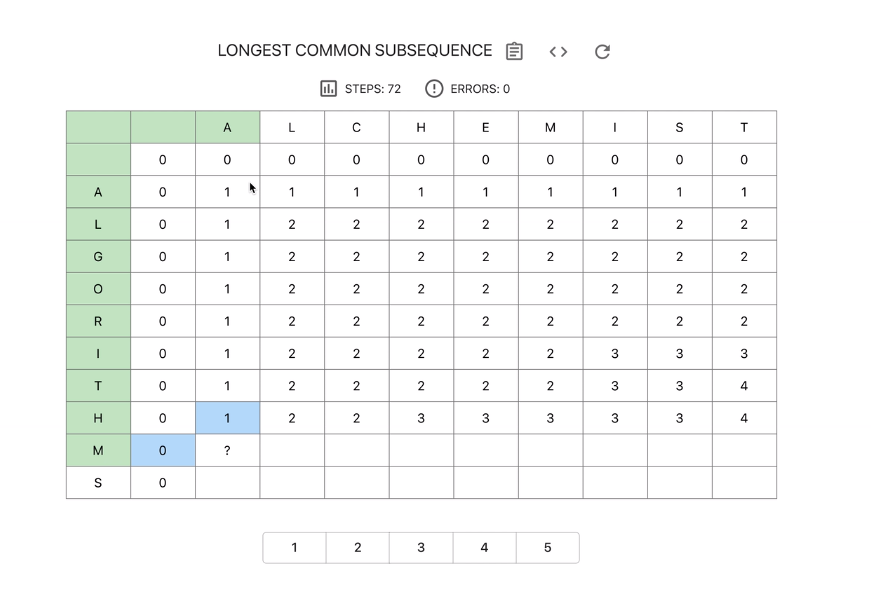
 根据两种不通情况得出两个式子：

dp[i][j] = dp[i-1][j-1] + 1

dp[i][j] = max(dp[i][j-1], dp[i-1][j])

代码实现：

class Solution:
    def LCS(self , s1: str, s2: str) -> str:
        # write code here
        m, n = len(s1), len(s2)
        dp = [[0]*(n+1) for _ in range(m+1)]  # 状态转移表【【0,0】,【0,0】,【0,0】】
        for i in range(1, m+1):
            for j in range(1, n+1):
                if s1[i-1] == s2[j-1]:  # 字符串索引从0开始
                    dp[i][j] = dp[i-1][j-1] + 1  # 当前dp格的值等于左上角的值+1 （相当于两个字符串当前指针指向的位置的公共子序列等于各自索引之前的字符串的公共子序列数加一）
                else:
                    dp[i][j] = max(dp[i][j-1], dp[i-1][j])
        # 回溯子序列，状态转移表往回推，相等
        ans = ''
        i, j = m,n
        while i > 0 and j > 0:  # 由于用i-1做比较所以只需要到1
            if s1[i-1] == s2[j-1]:
                ans += s1[i-1]
                i -= 1
                j -= 1
            elif dp[i][j-1] > dp[i-1][j]:
                j -= 1  # 那边大往那边移
            else:
                i -= 1
        if not ans : return -1
        return ans[::-1]

2.3  给定两个字符串str1和str2,输出两个字符串的最长公共子串
题目保证str1和str2的最长公共子串存在且唯一。 

示例1

输入： 
"1AB2345CD","12345EF"
返回值： 
"2345"

动态规划题解：

定义dp[i][j]表示字符串str1中第i个字符和str2种第j个字符为最后一个元素所构成的最长公共子串。如果要求dp[i][j]，也就是str1的第i个字符和str2的第j个字符为最后一个元素所构成的最长公共子串，我们首先需要判断这两个字符是否相等。

    • 如果不相等，那么他们就不能构成公共子串，也就是
      dp[i][j]=0;

    • 如果相等，我们还需要计算前面相等字符的个数，其实就是dp[i-1][j-1]，所以
      dp[i][j]=dp[i-1][j-1]+1；

时间复杂度：O（m*n），m和n分别表示两个字符串的长度

空间复杂度：O（m*n）

代码：

class Solution:
    def LCS(self , str1: str, str2: str) -> str:
        # write code here
        m, n = len(str1), len(str2)
        dp = [[0]*(n+1) for _ in range(m+1)]
        max_len = 0
        last_ind = 0
        for i in range(1, m+1):
            for j in range(1, n+1):
                if str1[i-1] == str2[j-1]:
                    dp[i][j] =  dp[i-1][j-1] + 1
                    if dp[i][j] > max_len:
                        max_len = dp[i][j]
                        last_ind = i
                else:
                    dp[i][j] =  0
        return str1[last_ind-max_len: last_ind]

动态规划代码优化：

上面我们使用的是二维数组，我们发现计算当前位置的时候之和左上角的值有关，所以我们可以把二维数组变为一维数组，注意第2个for循环要进行倒叙，因为后面的值要依赖前面的值，如果不倒叙，前面的值会被覆盖，导致结果错误

class Solution:
    def LCS(self , str1: str, str2: str) -> str:
        # write code here
        m, n = len(str1), len(str2)
        dp = [0]*(n+1)
        max_len = 0
        last_ind = 0
        for i in range(1, m+1):
            for j in range(n, 0, -1):
                if str1[i-1] == str2[j-1]:
                    dp[j] =  dp[j-1] + 1
                    if dp[j] > max_len:
                        max_len = dp[j]
                        last_ind = i
                else:
                    dp[j] =  0
        return str1[last_ind-max_len: last_ind]

时间复杂度：O（m*n），m和n分别表示两个字符串的长度

空间复杂度：O（n），只需要一个一维数组即可

动态规划方法在leetcode或牛客做题，python可能会导致运行超时，其它语言没问题，另外可以用，

滑动截取子串法：

  1. 界定左界限left
  2. i是随着循环次数往后移的这个没问题，为什么left不用每次循环之初清零让这个窗口从头来呢？
  3. 在我的理解中left不更新从头再来是没有必要的，因为如果left没问题的话就继续走了，感觉也是被截断那种连不上就从现在开始再来一遍
class Solution:
    def LCS(self , str1: str, str2: str) -> str:
        # write code here
        left = 0
        for i in range(len(str1)+1):
            if str1[i-left:i] in str2:
                res = str1[i-left:i]
                left += 1
        return res

 2.4 求路径：

一个机器人在m×n大小的地图的左上角（起点）。
机器人每次可以向下或向右移动。机器人要到达地图的右下角（终点）。
可以有多少种不同的路径从起点走到终点？
备注：m和n小于等于100,并保证计算结果在int范围内
 
数据范围：0 < n,m \le 1000<n,m≤100，保证计算结果在32位整型范围内
要求：空间复杂度 O(nm)O(nm)，时间复杂度 O(nm)O(nm)
进阶：空间复杂度 O(1)O(1)，时间复杂度 O(min(n,m))O(min(n,m))

示例1

输入： 
2,1
返回值： 
1

示例2

输入： 
2,2
返回值： 
2

题解：

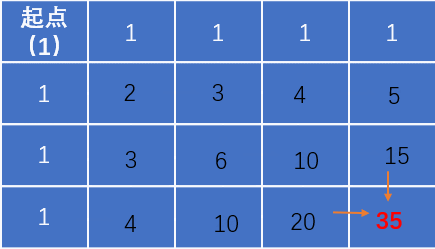
代码：

class Solution:
    def uniquePaths(self , m: int, n: int) -> int:
        # write code here
        dp = [[1]*n for row in range(m)]
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]return dp[m-1][n-1]

  2.5 矩阵的最小路径和：

给定一个 n * m 的矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。
 
数据范围: 1 \le n,m\le 5001≤n,m≤500，矩阵中任意值都满足 0 \le a_{i,j} \le 1000≤ai,j​≤100
要求：时间复杂度 O(nm)O(nm)
例如：当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时，对应的返回值为12，
所选择的最小累加和路径如下图所示：
题解：
分析之后得出状态转移方程:
1. 当i =0时：dp[i][j] = dp[i][j-1]  + matrix[i][j]
2. 当j =0时：dp[i][j] = dp[i-1][j]  + matrix[i][j]
3. 当i,j>0时：dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + matrix[i][j]

 代码：

class Solution:
    def minPathSum(self , matrix: List[List[int]]) -> int:
        # write code here
        m, n = len(matrix), len(matrix[0])
        dp = [[0]*(n+1) for _ in range(m+1)]
        for i in range(1, m+1):
            for j in range(1, n+1):
                if i == 1:
                    dp[i][j] = dp[i][j-1]  + matrix[i-1][j-1]  # 注意索引映射到matrix里时，i=i-1
                elif j == 1:
                    dp[i][j] = dp[i-1][j]  + matrix[i-1][j-1]
                else:
                    dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + matrix[i-1][j-1]
        return dp[-1][-1]

观察发现matrix可以直接作为dp矩阵，可以在原矩阵上修改，所以还可以优化代码节省空间，这里就不列出了。

 



posted @ 2022-03-22 20:25  清风_Z  阅读(72)  评论(0)  编辑  收藏  举报