01、算法入门

一、算法相关概念

一、什么是算法

非形式地说，算法(algorithm)就是任何定义的基数按过程，该过程取某个值或值的集合作为输入并产生某个值或值的集合作为输出。

我们可以把算法看成是用于求解良说明的计算问题的工具。

算法： 一个计算过程解决问题的方法

 二、时间复杂度

时间复杂度是用来估计算法运行时间的一个式子（单位）。

一般来说，时间复杂度高的算法比时间复杂度低的算法慢。　　

常见的时间复杂度（按效率排序）

不常见的时间复杂度

如何一眼判断时间复杂度

三、空间复杂度

空间复杂度： 用来评估算法内存占用大小的一个式子。

现在算法注重时间复杂度的优化，不太重视空间复杂度，有用“空间换时间”之说

二、递归 

当一个问题的解决可以依赖于其子问题的解决的时候，可以用递归。

python中最大深度理论1000，实际998不到

两个特点：

　　调用自身

　　结束条件

实例：

# 递归调用
def func(num):
    if num > 0:
        func(num - 1)
        print(num)
func(3)  # 1,2,3

4.1、斐波那契数列

从第三项开始，前两项之和等于后一项1,1,2,3,5,8 | 1,2,3,5,8

计算斐波那契数列第n项数是多少，这里以0项开始。

# 1.递归实现 时间复杂度 O(2^n)
def fib(n):
    if n == 0 or n == 1:
        return 1
    else:
        return fib(n - 1) + fib(n - 2)


# 2.循环实现O(n)，开了新空间
def fib2(n):
    li = [1, 1]
    for i in range(2, n + 1):
        li.append(li[-1] + li[-2])  # 列表最后两项就是要求的项的前两项
    return li[-1]


# 3.去掉递归的重复调用实现O(n), 但不能避免递归最大深度,且开了新空间
def fib3(n):
    li = [-1 for i in range(n + 1)]  # 记录

    def fib(n):
        if n == 0 or n == 1:
            return 1
        elif li[n] >= 0:
            return li[n]  # 直接返回不用重复递归
        else:
            v = fib(n - 1) + fib(n - 2)
            li[n] = v
            return li[n]

    return fib(n)


# 4.又省时间O(n)，又省空间的写法O(1)
def fib4(n):
    a = 1
    b = 1
    c = 1
    for i in range(2, n + 1):
        c = a + b
        a = b
        b = c
    return c

#5.还可以用通项公式实现，时间复杂度为O(1),但由于计算机存根号5时只能存小数，
# 所以存在误差，大概到n=69后数就不对了。


# 计算函数执行时间的装饰器
import time
def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__, t2-t1))
        return result
    return wrapper

# 由于装饰的函数递归会多次调用装饰器，给被装饰的函数套一层壳防止多次调用装饰器
@cal_time
def fibnacci(n):
    return fib4(n)


print(fibnacci(5))

4.2、汉诺塔问题

当一个问题的解决可以依赖于其子问题的解决的时候，可以用递归解决。

当盘子数n=2时 

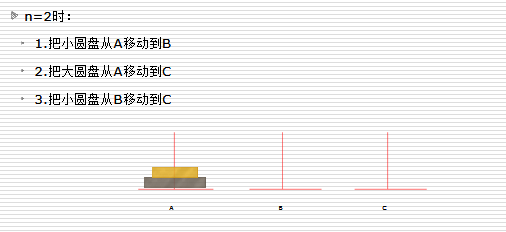
n个盘子时：

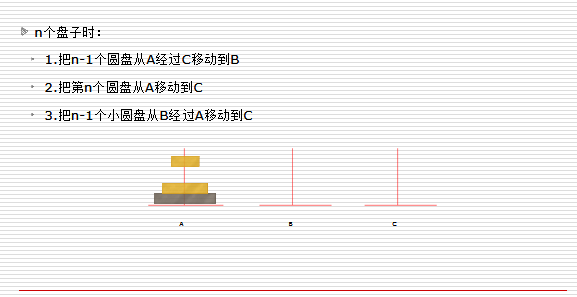
所以用代码实现就是：

def hanoi(n, A, B, C):
    """
    :param n: 盘子数
    :param A,B,C: 柱子
    """
    if n > 0:
        # 把n-1个盘子，从A经过C，移动到B
        hanoi(n-1, A, C, B)
        # 把第n个盘子从A,移动到C
        print('moving from %s to %s'%(A, C))
        # 把n-1个盘子，从B经过A，移动到C
        hanoi(n-1, B, A, C)


hanoi(3,"A","B","C")
# moving from A to C
# moving from A to B
# moving from C to B
# moving from A to C
# moving from B to A
# moving from B to C
# moving from A to C

4.3,例题

 

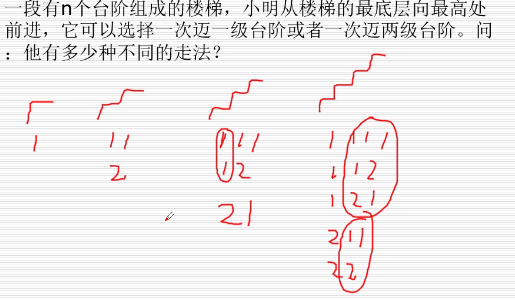
def f(n):
    '''
    :param n: 几级台阶
    :return: 多少种走法
    '''
    li = [1,1]
    for i in range(2,n+1):
        li.append(li[-1]+li[-2])
    return li[-1]

print(f(4))  # 5

三、查找

列表查找：从列表中查找指定元素

输入：列表、待查找元素

输出：元素下标或未查找到元素

顺序查找：从列表第一个元素开始，顺序进行搜索，直到找到为止。

def linear_search(data_set, value):
     for i in range(range(data_set)):   
        if data_set[i] == value:
          return i
    return
# 时间复杂度O(n)

二分查找：

　　从有序列表的候选区data[0:n] 开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半

def binary_search(li, val):
    low = 0
    high = len(li) - 1
    while low <= high:
        mid = (low + high) // 2
        if li[mid] == val:
            return mid
        elif li[mid] > val:
            high = mid - 1
        else:  # li[mid] < val
            low = mid + 1
    return -1  # 没找到
# 时间复杂度 O(logn)

# 测试
print(binary_search([1,2,3,8,9,45,66,78],45))  # 5
print(binary_search([1,2,3,8,9,45,66,78],7))  # -1