《P7842 「PMOI-4」可怜的团主》
div2的T3我就爬了orz........
摸了半天只想出来了一个40分的做法:
第一1的判断:暴力dfs,感觉可以记忆化一下a的前缀再剪一下枝。不过数据大还是会T掉。
对于2的判断,我这个根据入度去贪心维护,感觉上复杂度和正确性都是在线的好像。

// Author: levil #include<bits/stdc++.h> using namespace std; typedef long long LL; typedef pair<int,int> pii; const int N = 1e3 + 5; const int M = 5e5 + 5; const LL Mod = 1e9 + 7; #define pi acos(-1) #define INF 1e9 #define dbg(ax) cout << "now this num is " << ax << endl; namespace FASTIO{ inline int read(){ int x = 0,f = 1;char c = getchar(); while(c < '0' || c > '9'){if(c == '-') f = -1;c = getchar();} while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();} return x*f; } } using namespace FASTIO; int n,m,in[N]; vector<int> G[N],vec[N]; bool vis[N]; vector<string> tmp; map<string,int> mp; void dfs(int x,int u,string a,int up) { if(tmp.size() == up) return ; if(x == n + 1) { string b = a; reverse(a.begin(),a.end()); if(mp[a] == 1 || mp[b] == 1) return ; tmp.push_back(b); mp[b] = 1; return ; } for(auto v : G[u]) { if(!vis[v]) { vis[v] = 1; dfs(x + 1,v,a + to_string(v),up); vis[v] = 0; } } } vector<int> check2(int sz) { priority_queue<pii,vector<pii>,greater<pii> > Q; for(int i = 1;i <= n;++i) Q.push(pii{in[i],i}); vector<int> ans; while(!Q.empty()) { pii q = Q.top(); Q.pop(); int u = q.second; if(vis[u]) continue; vis[u] = 1; ans.push_back(u); if(ans.size() == sz) break; for(auto v : G[u]) { if(vis[v]) continue; vis[v] = 1; for(auto tt : G[v]) { if(!vis[tt]) { in[tt]--; Q.push(pii{in[tt],tt}); } } } } return ans; } void solve() { n = read(),m = read(); int lim1 = (n + 5) / 6,lim2 = n / 3; while(m--) { int u,v;u = read(),v = read(); G[u].push_back(v),G[v].push_back(u); in[u]++,in[v]++; } vector<int> ans = check2(lim2); if(ans.size() == lim2) { printf("2\n"); for(int i = 0;i < ans.size();++i) printf("%d%c",ans[i],i == ans.size() - 1 ? '\n' : ' '); } else { for(int i = 1;i <= n;++i) { if(tmp.size() < lim1) { vis[i] = 1; dfs(2,i,to_string(i),lim1); vis[i] = 0; } } if(tmp.size() == lim1) { printf("1\n"); for(auto v : tmp) { string t = v; printf("%d",n); for(auto vv : t) printf(" %c",vv); printf("\n"); } } else printf("Poor lnlhm!\n"); } } int main() { solve(); //system("pause"); return 0; }
100分的做法:
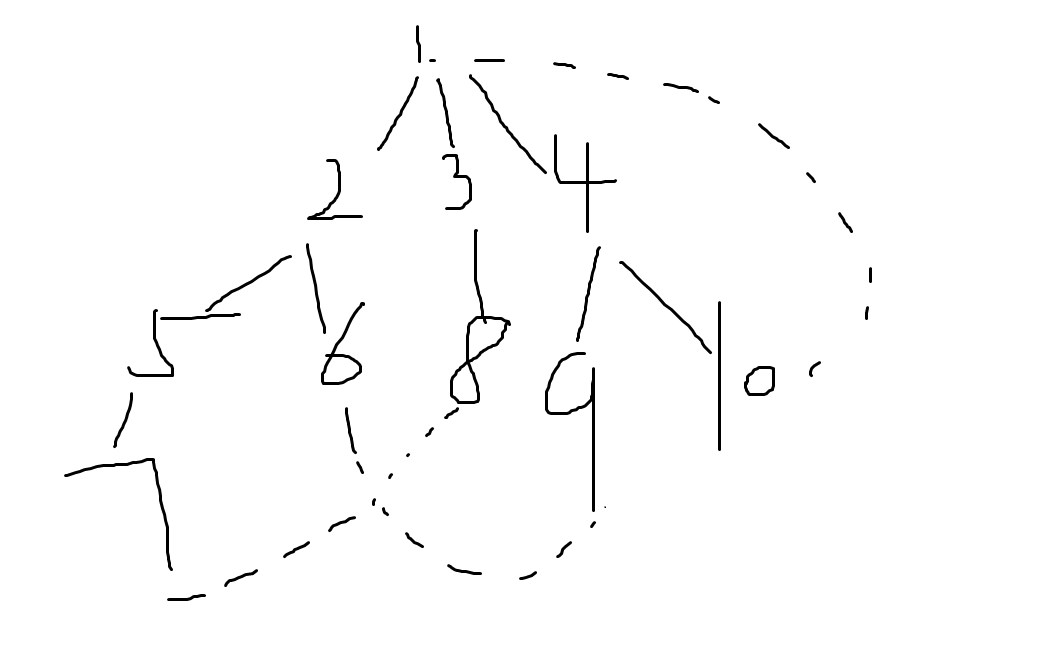
考虑找到原图的dfs树:可以知道dfs树上的叶子之间必定是两两没有连边的。
那么对于我们操作1的答案就是选出所有的叶子,如果这里的叶子 < $\left \lfloor \frac{n}{3} \right \rfloor$
那么他们两两配对的组合数量就一定 <= $\left \lceil \frac{n}{6} \right \rceil$这个可以算一下..
那么如果不够,我们就直接加入单点来表示一条路径就行了,那么这个总数量肯定可以达到$\left \lceil \frac{n}{6} \right \rceil$
那么对于第二种方案的打印和配对。
我们可以考虑一棵dfs序树:我们可以发现要覆盖到所有的节点,那么我们的路径方案最好就是按dfs序来,因为每个子树内dfs序连续。
所有不同子树之间的dfs序也是递增的,我们让左一半去连接右边一半,这样保证每个节点都能覆盖到,最后没得匹配的叶子连接根,保证到叶子路径上的全覆盖。
注意的是,我们应该要保证所有的叶子都能匹配完,所以我们在最后都加入一个根节点1,若加入后还是奇数个,那么再加入一次保证都有配对。

// Author: levil #include<bits/stdc++.h> using namespace std; typedef long long LL; typedef pair<int,int> pii; const int N = 1e3 + 5; const int M = 5e5 + 5; const LL Mod = 1e9 + 7; #define pi acos(-1) #define INF 1e9 #define dbg(ax) cout << "now this num is " << ax << endl; namespace FASTIO{ inline int read(){ int x = 0,f = 1;char c = getchar(); while(c < '0' || c > '9'){if(c == '-') f = -1;c = getchar();} while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();} return x*f; } } using namespace FASTIO; int n,m,dfn[N],fa[N],tim = 0,tot = 0; vector<int> G[N]; int vec[N],dep[N]; void dfs(int u,int ffa) { dfn[u] = ++tim; dep[u] = dep[ffa] + 1; fa[u] = ffa; int f = 0; for(auto v : G[u]) if(!dfn[v]) dfs(v,u),f = 1; if(f == 0) vec[++tot] = u; } void dfs2(int x,int y) { vector<int> ans1,ans2; while(x != y) { if(dep[x] > dep[y]) ans1.push_back(x),x = fa[x]; else ans2.push_back(y),y = fa[y]; } ans1.push_back(x); reverse(ans2.begin(),ans2.end()); printf("%d",ans1.size() + ans2.size()); for(auto v : ans1) printf(" %d",v); for(auto v : ans2) printf(" %d",v); printf("\n"); } bool cmp(int x,int y) { return dfn[x] < dfn[y]; } void solve() { n = read(),m = read(); int lim1 = (n + 5) / 6,lim2 = n / 3; while(m--) { int u,v;u = read(),v = read(); G[u].push_back(v),G[v].push_back(u); } dfs(1,0); if(tot >= lim2) { printf("2\n"); for(int i = 1;i <= lim2;++i) printf("%d%c",vec[i],i == lim2 ? '\n' : ' '); } else { printf("1\n"); vec[++tot] = 1; if(tot % 2 != 0) vec[++tot] = 1; int cnt = 0; for(int i = 1;i <= tot / 2;++i) { if(cnt == lim1) break; dfs2(vec[i],vec[i + tot / 2]),++cnt; } for(int i = 1;i <= n;++i) { if(cnt == lim1) break; printf("1 %d\n",i); ++cnt; } } } int main() { solve(); // system("pause"); return 0; } /* 6 5 1 2 1 3 2 4 2 5 3 6 */



