《2017 Multi-University Training Contest 1》
Add More Zero:
题目让我们求最大的k满足,10 ^ k <= 2 ^ m - 1
即求10 ^ k < 2 ^ m
取对数k * lg10 < m * lg2
k < m * lg2 / lg 10

// Author: levil #include<iostream> #include<stdio.h> #include<queue> #include<algorithm> #include<math.h> #include<stack> #include<map> #include<limits.h> #include<vector> #include<string.h> #include<string> using namespace std; typedef long long LL; typedef unsigned long long ULL; typedef pair<int,int> pii; const int N = 1e5 + 5; const int M = 1e7 + 5; const LL Mod = 1e12; #define pi acos(-1) #define INF 1e12 #define dbg(ax) cout << "now this num is " << ax << endl; namespace FASTIO{ inline LL read(){ LL x = 0,f = 1;char c = getchar(); while(c < '0' || c > '9'){if(c == '-') f = -1;c = getchar();} while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();} return x*f; } } using namespace FASTIO; int main() { int m,ca = 0; while(cin >> m) { int ans = m * 1.0 * log(2) / log(10); printf("Case #%d: %d\n",++ca,ans); } // system("pause"); return 0; }
Balala Power!:
这个题也挺有意思的,做的时候猜测到了贪心策略就是按整个的数值的大小赋值,代价肯定是最优的,这个结论很好证明 (相邻两个位证明一下)。
但是问题主要是单按给出的数值来赋值会爆long long,所以就要考虑按最高位比较。
这里就有一步非常重要的操作了就是要进位,这样才保证了按最高位往下比较的值肯定满足最大性质。

// Author: levil #include<iostream> #include<stdio.h> #include<queue> #include<algorithm> #include<math.h> #include<stack> #include<map> #include<limits.h> #include<vector> #include<string.h> #include<string> using namespace std; typedef long long LL; typedef unsigned long long ULL; typedef pair<int,int> pii; const int N = 1e5 + 5; const int M = 1e7 + 5; const LL Mod = 1e9 + 7; #define pi acos(-1) #define INF 1e12 #define dbg(ax) cout << "now this num is " << ax << endl; namespace FASTIO{ inline LL read(){ LL x = 0,f = 1;char c = getchar(); while(c < '0' || c > '9'){if(c == '-') f = -1;c = getchar();} while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();} return x*f; } } using namespace FASTIO; LL mu[N],val[30],all[30]; bool vis[30],tag[30]; struct Node{ int cc,cnt[N]; }p[30]; bool cmp(Node a,Node b) { for(int i = N - 1;i >= 0;--i) { if(a.cnt[i] != b.cnt[i]) { return a.cnt[i] > b.cnt[i]; } } return false; } void init() { mu[0] = 1; for(int i = 1;i < N;++i) mu[i] = mu[i - 1] * 26 % Mod; } int main() { init(); int n,ca = 0; ios::sync_with_stdio(false); while(cin >> n) { for(int i = 0;i < 26;++i) { for(int j = 0;j < N;++j) { p[i].cnt[j] = 0; } p[i].cc = i; vis[i] = val[i] = all[i] = tag[i] = 0; } for(int i = 1;i <= n;++i) { string s;cin >> s; int len = s.size(); for(int j = 0;j < len;++j) { int c = s[len - j - 1] - 'a'; p[c].cnt[j]++; all[c] = (all[c] + mu[j]) % Mod; } if(len > 1) vis[s[0] - 'a'] = 1; } //进位 for(int i = 0;i < 26;++i) { for(int j = 0;j < N;++j) { if(j != N - 1) p[i].cnt[j + 1] += p[i].cnt[j] / 26; p[i].cnt[j] %= 26; } } sort(p,p + 26,cmp); int col = 25; LL ans = 0; for(int i = 25;i >= 0;--i) { if(vis[p[i].cc] != 1) { tag[p[i].cc] = 1; break; } } for(int i = 0;i < 26;++i) { if(tag[p[i].cc] != 1) { val[p[i].cc] = col--; } } for(int i = 0;i < 26;++i) { ans = ans + 1LL * val[p[i].cc] * all[p[i].cc] % Mod; ans %= Mod; } printf("Case #%d: %lld\n",++ca,ans); } // system("pause"); return 0; } /* 5 aabbcc abc afaf zzda dad 3 aabbcc abc afaf */
KazaQ's Socks:
这题比较简单,最后一个位置很显然只有n 和 n - 1两种可能,对于前面的都一直循环。

// Author: levil #include<iostream> #include<stdio.h> #include<queue> #include<algorithm> #include<math.h> #include<stack> #include<map> #include<limits.h> #include<vector> #include<string.h> #include<string> using namespace std; typedef long long LL; typedef unsigned long long ULL; typedef pair<int,int> pii; const int N = 1e5 + 5; const int M = 1e7 + 5; const LL Mod = 1e12; #define pi acos(-1) #define INF 1e12 #define dbg(ax) cout << "now this num is " << ax << endl; namespace FASTIO{ inline LL read(){ LL x = 0,f = 1;char c = getchar(); while(c < '0' || c > '9'){if(c == '-') f = -1;c = getchar();} while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();} return x*f; } } using namespace FASTIO; int main() { int caa = 0; LL n,k; while(cin >> n >> k) { printf("Case #%d: ",++caa); if(k <= n) printf("%lld\n",k); else { k -= n; LL ma = k % (n - 1); LL tmp = k / (n - 1); if(ma == 0) { printf("%lld\n",tmp % 2 != 0 ? n - 1 : n); } else { printf("%lld\n",ma); } } } // system("pause"); return 0; }
Limited Permutation:
这题真的非常优秀,一开始题目一直没读懂。
题意是求:满足所有的L[i],r[i]的排列数量。
贯穿本题目的很重要的一个信息,就是if and only if,他的意思就是说明对于任意pi,a[L + 1]位置和a[r + 1]位置肯定都 < pi.
那么这里就出现了一个很重要的信息,就是区间不会交叉,如果区间交叉。
那么对于a[i],a[j]就会出现不合法的情况,这里可以画一画就能明白。
然后就是本题的一个重要信息,就是对于pi的区间L[i],r[i],以pi为中心,一定存在区间[L[i],pi - 1]和[pi + 1,r[i]]。
也就是子区间必定是这个两个。
证明:假定左区间的最小值位置为x,右区间的最小值位置为y。
因为一共有n个区间,n个数,并且不可相交,所以每个数都肯定会被包含在一个区间内。
那么对于L[i] ~ pi,这段区间的最小值为x,那么很显然由于if and only if的存在,那么它若存在一定是以L[i],pi - 1为边界。
右边同理。所以满足该性质。
有了这一性质,我们就可以递归分治地处理左右子区间,很显然的是pi的值 < 左右区间的最小值。
所以我们每次都放最小的给父节点,然后剩下的排列组合分配。
那么 ans(fa) = ans(Lson) * ans(rson) * C(fa的sz,Lson的sz)。
这题到这还不算完,因为这里的输入究极恶心,必须要读入挂不然速度不够。
然后处理EOF的问题又导致我有些读入挂不行。
而且如果是递归的写法,会出现爆炸的问题,此时需要用
#pragma comment(linker, /STACK:102400000,102400000)来扩大hdu测评的栈区。
或者就不写递归的做法。

// Author: levil #pragma comment(linker, /STACK:102400000,102400000) #include<iostream> #include<stdio.h> #include<queue> #include<algorithm> #include<math.h> #include<stack> #include<map> #include<limits.h> #include<vector> #include<string.h> #include<string> using namespace std; typedef long long LL; typedef pair<int,int> pii; const int N = 1e6 + 5; const int M = 2e6 + 5; const LL Mod = 1e9 + 7; #define pi acos(-1) #define INF 1e9 #define dbg(ax) cout << "now this num is " << ax << endl; namespace IO { const int MX = 4e7; //1e7占用内存11000kb char buf[MX]; int c, sz; void begin() { c = 0; sz = fread(buf, 1, MX, stdin); } inline bool read(int &t) { while(c < sz && buf[c] != '-' && (buf[c] < '0' || buf[c] > '9')) c++; if(c >= sz) return false; bool flag = 0; if(buf[c] == '-') flag = 1, c++; for(t = 0; c < sz && '0' <= buf[c] && buf[c] <= '9'; c++) t = t * 10 + buf[c] - '0'; if(flag) t = -t; return true; } } int L[N],r[N],f[N],inv[N]; map<pii,int> mp; LL quick_mi(LL a,LL b) { LL re = 1; while(b) { if(b & 1) re = re * a % Mod; a = a * a % Mod; b >>= 1; } return re; } void init() { f[0] = 1; for(int i = 1;i < N;++i) f[i] = 1LL * f[i - 1] * i % Mod; inv[N - 1] = quick_mi(f[N - 1],Mod - 2); for(int i = N - 2;i >= 0;--i) inv[i] = 1LL * inv[i + 1] * (i + 1) % Mod; } LL C(int n,int m) { return 1LL * f[n] * inv[n - m] % Mod * inv[m] % Mod; } LL dfs(int ll,int rr) { if(ll > rr) return 1;//这里不能取到等于,因为等于的时候也要判断是否存在这个区间即map[x,x]是否存在 int pos = mp[pii{ll,rr}]; if(pos == 0) return 0; LL ma = dfs(ll,pos - 1) * dfs(pos + 1,rr) % Mod * C(rr - ll,pos - ll) % Mod; return ma; } int main() { init(); int n,ca = 0; IO::begin(); while(IO::read(n)) { mp.clear(); for(int i = 1;i <= n;++i) IO::read(L[i]); for(int i = 1;i <= n;++i) IO::read(r[i]); for(int i = 1;i <= n;++i) { mp[pii{L[i],r[i]}] = i; } LL ans = dfs(1,n); printf("Case #%d: %lld\n",++ca,ans); } //system("pause"); return 0; }
Colorful Tree:
又被折磨啦。
一开始想的只需要处理子树,但是后面想了下任意子树之间都可以连成路径,于是去考虑单颜色的贡献,但是总是感觉差一点。
正解:首先肯定是考虑单个颜色的贡献,即统计包含该种颜色的路径有多少条。
但是这个数量还是很难计算,于是正难则反,我们考虑去统计不包含该颜色的路径数。
那么sum[包含] = n * (n - 1) / 2 - sum[不包含]。这个就是对于该颜色包含的路径方案数。
对于计算不包含的方案数:考虑成连通块的形式,对于这个不包含该颜色的连通块,若数量为sz个,那么可以组成的方案数就是C(sz,2)种。
那么这个连通块的大小怎么算?对于以颜色x为根的子树u,假设已经维护好了它的子树中以所有以x为根的子树大小sz(all)。那么sz[连通块] = sz(u) - sz(all)。
可以画几种例子就能明白。但是我们这样其实只是维护了子树中的方案数,还可能存在跨越根节点1的方案数,所以最后还要遍历一次去计算跨越的方案数。
对于这里的以颜色x为根的子树大小,我用了线段树合并来维护。

// Author: levil #include<bits/stdc++.h> using namespace std; typedef long long LL; typedef pair<int,int> pii; const int N = 2e5 + 5; const int M = 2e6 + 5; const LL Mod = 1e9 + 7; #define pi acos(-1) #define INF 1e9 #define dbg(ax) cout << "now this num is " << ax << endl; int n,top = 0,c[N],rt[N],sz[N]; LL tmp[N]; bool vis[N]; vector<int> G[N]; struct Node{int L,r;LL sum;}node[N * 20]; int build(int L,int r,int x) { int idx = ++top; if(L == r) { node[idx].sum = 1; return idx; } int mid = (L + r) >> 1; if(mid >= x) node[idx].L = build(L,mid,x); else node[idx].r = build(mid + 1,r,x); return idx; } int Union(int x,int y,int L,int r) { if(x == 0) return y; if(y == 0) return x; if(L == r) {//因为存在下一层的性质,要对最下面做特判 node[x].sum += node[y].sum; return x; } int mid = (L + r) >> 1; node[x].L = Union(node[x].L,node[y].L,L,mid); node[x].r = Union(node[x].r,node[y].r,mid + 1,r); node[x].sum = node[node[x].L].sum + node[node[x].r].sum; return x; } void update(int L,int r,int x,LL val,int idx) { if(L == r) { node[idx].sum = val; return ; } int mid = (L + r) >> 1; if(mid >= x) update(L,mid,x,val,node[idx].L); else update(mid + 1,r,x,val,node[idx].r); } LL query(int L,int r,int x,int idx) { if(idx == 0) return 0; if(L == r) return node[idx].sum; int mid = (L + r) >> 1; if(mid >= x) return query(L,mid,x,node[idx].L); else return query(mid + 1,r,x,node[idx].r); } void dfs(int u,int fa) { sz[u] = 1; for(auto v : G[u]) { if(v == fa) continue; dfs(v,u); sz[u] += sz[v]; LL cnt = sz[v] - query(1,n,c[u],rt[v]); if(cnt >= 2) { tmp[c[u]] += cnt * (cnt - 1) / 2; } rt[u] = Union(rt[u],rt[v],1,n); } update(1,n,c[u],sz[u],rt[u]); } int main() { int ca = 0; while(~scanf("%d",&n)) { for(int i = 1;i <= n;++i) G[i].clear(),rt[i] = 0,sz[i] = 0,vis[i] = 0,tmp[i] = 0; top = 0; for(int i = 1;i <= n;++i) scanf("%d",&c[i]),vis[c[i]] = 1; for(int i = 1;i <= n;++i) rt[i] = build(1,n,c[i]); for(int i = 1;i < n;++i) { int x,y; scanf("%d %d",&x,&y); G[x].push_back(y); G[y].push_back(x); } dfs(1,0); LL ans = 0,ma = 0; for(int i = 1;i <= n;++i) { if(vis[i] == 0) continue; LL cnt = sz[1] - query(1,n,i,rt[1]); //printf("col is %d tmp is %lld query is %lld\n",i,tmp[i],query(1,n,i,rt[1])); ans += tmp[i]; if(cnt >= 2) ans += cnt * (cnt - 1) / 2; ma += 1LL * n * (n - 1) / 2; } ans = ma - ans; printf("Case #%d: %lld\n",++ca,ans); for(int i = 1;i <= top;++i) node[i].L = node[i].r = 0; } // system("pause"); return 0; } /* 12 1 2 3 1 2 2 2 1 1 3 3 2 1 2 1 3 2 4 2 5 4 7 5 8 8 11 11 12 3 6 6 9 6 10 */
Hints of sd0061:
基本想到思路了。显然这里的关键信息就是b[i] + b[j] <= b[k]。
也就是说这里的b数组如果排序之后必定是呈现类似斐波那契数列的增长速度。
在36位之后就超过了1e7,但m最大100,那么显然会有很多重复。
对于查询的操作,显然sort复杂度不够。这里就要用到nth_element。
它在查询到区间第k小之后,还具有一个性质,就是在这段区间中k左边的都小于它,右边的都大于它。
那么我们就可以先对询问排序,然后每次都缩小对下一次查询的区间大小。
但是这里如果正向去缩小,复杂度依旧不够,因为很显然正向开始的询问值都很小,对区间的大小减少没有什么影响。
这就导致了一开始查询的区间都过大,那么我们就考虑反向来,每次都减少较大的区间大小。
PS:这里nth_element一直记成了k要-1,导致一直wa,真是个傻子。还有个细节就是要用%u来输入输出,不然还是wa,因为是unsigned类型,范围和int有点不一样

// Author: levil #include<bits/stdc++.h> using namespace std; typedef long long LL; typedef pair<int,int> pii; const int N = 1e7 + 5; const int M = 2e6 + 5; const LL Mod = 1e9 + 7; #define pi acos(-1) #define INF 1e9 #define dbg(ax) cout << "now this num is " << ax << endl; int n,m; unsigned solve(unsigned &x,unsigned &y,unsigned &z) { unsigned t; x ^= x << 16; x ^= x >> 5; x ^= x << 1; t = x; x = y; y = z; z = t ^ x ^ y; return z; } unsigned a[N],A,B,C; struct Node{ int id,val; bool operator < (const Node &a)const{ return val < a.val; } unsigned ans; }b[105]; bool cmp(Node a,Node b) { return a.id < b.id; } int main() { int ca = 0; while(~scanf("%d %d %u %u %u",&n,&m,&A,&B,&C)) { for(int i = 1;i <= m;++i) scanf("%d",&b[i].val),b[i].id = i; unsigned x = A, y = B, z = C; for(int i = 1;i <= n;++i) a[i] = solve(x,y,z); sort(b + 1,b + m + 1); nth_element(a + 1,a + b[m].val + 1,a + n + 1); b[m].ans = a[b[m].val + 1]; for(int i = m - 1;i >= 1;--i) { if(b[i].val == b[i + 1].val) { b[i].ans = b[i + 1].ans; continue; } nth_element(a + 1,a + b[i].val + 1,a + b[i + 1].val + 1 + 1); b[i].ans = a[b[i].val + 1]; } sort(b + 1,b + m + 1,cmp); printf("Case #%d: ",++ca); for(int i = 1;i <= m;++i) printf("%u%c",b[i].ans,i == m ? '\n' : ' '); } // system("pause"); return 0; } /* 20 10 21121 3552121 12154512 15 4 6 9 8 1 2 5 19 0 */
Function:
读题又爆炸了。是计算函数的数量。
第一眼看到就觉得和置换群有关系,我们以样例二为例子。
f[0] = b[f[a[0]]] = b[f[2]]
f[1] = b[f[a[1]]] = b[f[0]]
f[2] = b[f[a[2]]] = b[f[1]]
我们可以发现,0 1 2 - 2 0 1对应形成一个循环群。
所以我们可以知道,函数的每一段一定是一个循环群。
可见如果我们知道了一个循环群中的任意一个数,其他的也就可以推导出来。
所以我们的方案数就是把a中的所有循环群配置好的不同方案数。
因为这里说了两个函数不同是只有一个位置不同即可。
那么对于一个函数中的多个循环群,可以用相同位置中b的循环群。
从上面可见,f[0] = b[f[2]] f[1] = bb[f[2]] f[2] = bbb[f[2]]。
这里可以发现,我们配对的a,b中的循环群长度必须满足,b是a的因子,这样才能保证对应a中的一个数在经过k * len(b)的变换后能回到自己。
而且这个配置的方案数为len(b),因为可以循环着调换位置。
所以方案数就是所有a中的循环群配置方案数的累积。

// Author: levil #include<bits/stdc++.h> using namespace std; typedef long long LL; typedef pair<int,int> pii; const int N = 1e5 + 5; const int M = 2e6 + 5; const LL Mod = 1e9 + 7; #define pi acos(-1) #define INF 1e9 #define dbg(ax) cout << "now this num is " << ax << endl; int n,m,a[N],b[N],ca = 0; int lp1[N],lp2[N]; bool vis[N]; vector<int> vec1; int main() { while(~scanf("%d %d",&n,&m)) { for(int i = 0;i < n;++i) scanf("%d",&a[i]); for(int i = 0;i < m;++i) scanf("%d",&b[i]); memset(lp1,0,sizeof(lp1)); memset(lp2,0,sizeof(lp2)); memset(vis,0,sizeof(vis)); vec1.clear(); for(int i = 0;i < n;++i) { if(vis[a[i]]) continue; int len = 1; vis[a[i]] = 1; int st = a[i]; while(vis[a[st]] != 1) { vis[a[st]] = 1; st = a[st]; ++len; } lp1[len]++; vec1.push_back(len); } memset(vis,0,sizeof(vis)); for(int i = 0;i < m;++i) { if(vis[b[i]]) continue; int len = 1; vis[b[i]] = 1; int st = b[i]; while(vis[b[st]] != 1) { vis[b[st]] = 1; st = b[st]; ++len; } lp2[len]++; } LL ans = 1; for(auto v : vec1) {//a中第i个循环群 int m = sqrt(v); LL ma = 0; for(int j = 1;j <= m;++j) { if(v % j == 0) { ma = (ma + 1LL * j * lp2[j]) % Mod;//j种摆法 if(v / j != j) ma = (ma + 1LL * (v / j) * lp2[v / j]) % Mod; } } ans = ans * ma % Mod; } printf("Case #%d: %lld\n",++ca,ans); } system("pause"); return 0; }
I Curse Myself:
这题中间出了亿点点问题。一开始的切入点是生成树加边。
但是仔细看条件发现,每条边最多在一个简单环中,那么显然就存在两种情况:
1:这条边不在环上。
2:这条边在环上。
如果不在环上,那么显然必须要选入。
如果在环上,那么对于每个环,都可以删去一条边保证是一个生成树,注意这里是必须要删去一条(每个环),因为树是不能有环存在。
那么题目就抽象成给定k个环,每个环选一条边,组成最大的k种方案数,那么这就是经典的k路并归问题。
我们优先队列维护即可:这里有一个很重要的优化,没有就会超时。

void tarjan(int u,int fa) { dfn[u] = low[u] = ++tim; S.push(u); for(auto v : G[u]) { if(!dfn[v.to]) { tarjan(v.to,u); low[u] = min(low[u],low[v.to]); } else if(v.to != fa) low[u] = min(low[u],dfn[v.to]); } if(dfn[u] == low[u]) { ++cc; while(S.top() != u) { col[S.top()] = cc; S.pop(); } col[S.top()] = cc; S.pop(); } } void solve() { tarjan(1,0); for(int i = 1;i <= n;++i) { for(auto v : G[i]) { if(v.to < i || col[i] != col[v.to]) continue; vec[col[i]].push_back(v.dis); } } }
这就是有向图缩强连通分量的写法,但是这里并不能真正地缩环成功。
可以看一组例子:
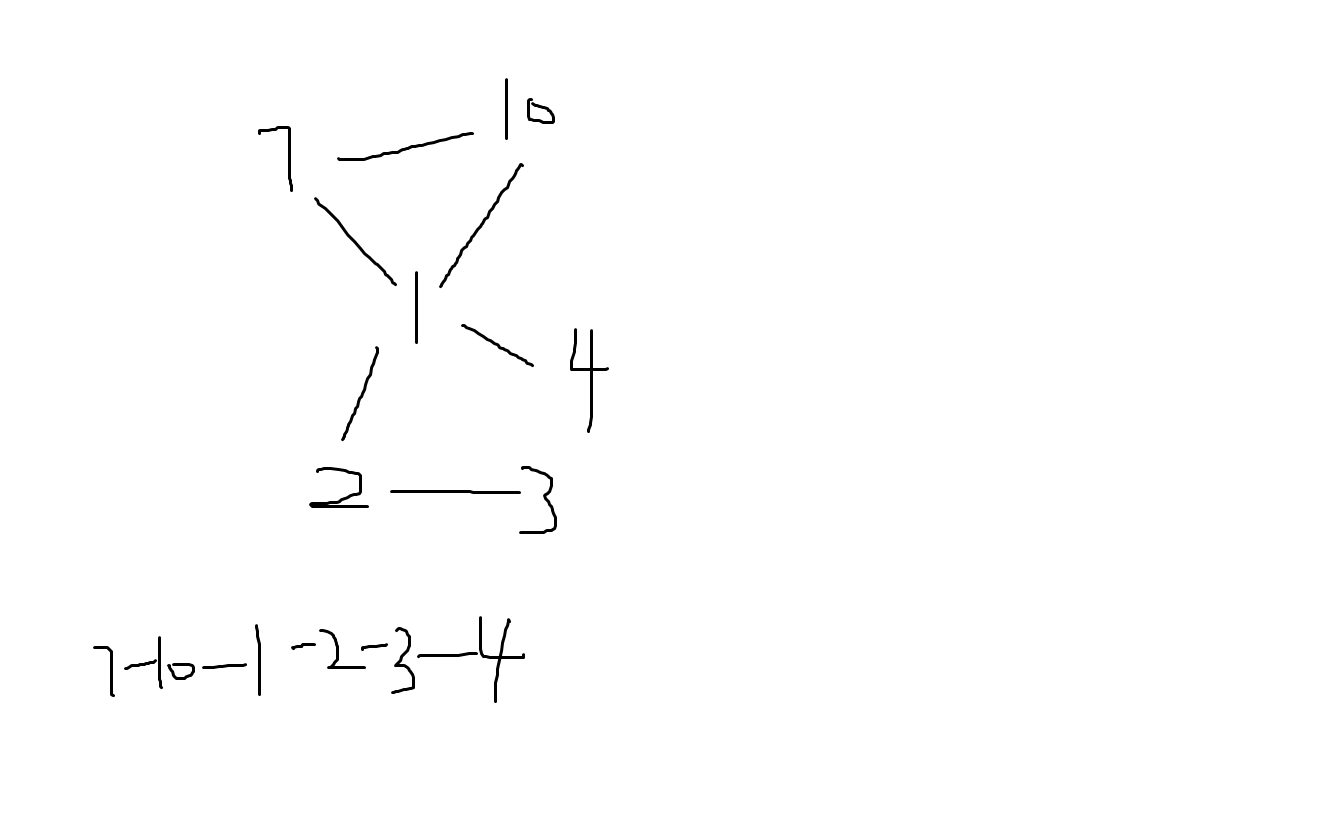

void tarjan(int u,int fa) { dfn[u] = ++tim; for(auto v : G[u]) { if(!dfn[v.to]) { ffa[v.to] = u; tarjan(v.to,u); } else if(v.to != fa && dfn[v.to] < dfn[u]) {//环尾部 int j = u; vec[++cc].push_back(v.dis); while(j != v.to) { vec[cc].push_back(d[j][ffa[j]]); j = ffa[j]; } } } }
这里的思路就是遇到了环尾部就开始退栈。
注意的是上面这种写法可行的条件是因为这是个仙人掌图。
仙人掌图:如果某个无向连通图的任意一条边至多只出现在一条简单回路(simple cycle)里,我们就称这张图为仙人图(cactus)。所谓简单回路就是指在图上不重复经过任何一个顶点的回路。
如果一条边可以存在在多个环里,那么显然无法缩环,因为我们无法确定地对每条边的归属。

// Author: levil #include<bits/stdc++.h> using namespace std; typedef long long LL; typedef pair<LL,int> pii; const int N = 1e3 + 5; const int M = 2e3 + 5; const LL Mod = 4294967296; #define pi acos(-1) #define INF 1e9 #define dbg(ax) cout << "now this num is " << ax << endl; struct Node{int to,dis;}; struct node{ int v,now; friend bool operator < (const node &x,const node &y) { return x.v < y.v; } }; vector<Node> G[N]; vector<int> ans,tf; int dfn[N],low[N],tim,col[N],hav[N],cc = 0,n,m,K,d[N][N],ffa[N]; vector<int> vec[N]; stack<int> S; void init(int n) { memset(dfn,0,sizeof(dfn)); memset(col,0,sizeof(col)); for(int i = 1;i <= n;++i) G[i].clear(),vec[i].clear(); cc = tim = 0; while(!S.empty()) S.pop(); } /*void tarjan(int u,int fa) { dfn[u] = low[u] = ++tim; S.push(u); for(auto v : G[u]) { if(!dfn[v.to]) { tarjan(v.to,u); low[u] = min(low[u],low[v.to]); } else if(v.to != fa) low[u] = min(low[u],dfn[v.to]); } if(dfn[u] == low[u]) { ++cc; while(S.top() != u) { col[S.top()] = cc; S.pop(); } col[S.top()] = cc; S.pop(); } }*/ void tarjan(int u,int fa) { dfn[u] = ++tim; for(auto v : G[u]) { if(!dfn[v.to]) { ffa[v.to] = u; tarjan(v.to,u); } else if(v.to != fa && dfn[v.to] < dfn[u]) { int j = u; vec[++cc].push_back(v.dis); while(j != v.to) { vec[cc].push_back(d[j][ffa[j]]); j = ffa[j]; } } } } void merge(vector<int> &a,vector<int> b) { tf.clear(); priority_queue<node> q; for(int i = 0;i < b.size();i++) q.push(node{a[0] + b[i],0}); while(tf.size() < K && !q.empty()){ node it = q.top(); q.pop(); tf.push_back(it.v); if(it.now + 1 < a.size()){ q.push(node{it.v - a[it.now] + a[it.now + 1],it.now + 1}); } } a = tf; } void solve() { tarjan(1,0); /*for(int i = 1;i <= n;++i) { for(auto v : G[i]) { if(v.to < i || col[i] != col[v.to]) continue; vec[col[i]].push_back(v.dis); } }*/ } int main() { int ca = 0; while(~scanf("%d %d",&n,&m)) { init(n); LL all = 0; for(int i = 1;i <= m;++i) { int x,y,z; scanf("%d %d %d",&x,&y,&z); G[x].push_back(Node{y,z}); G[y].push_back(Node{x,z}); d[x][y] = d[y][x] = z; all += z; } scanf("%d",&K); solve(); ans.clear(); ans.push_back(0); for(int i = 1;i <= cc;++i) { if(vec[i].size() != 0) merge(ans,vec[i]); } LL ma = 0; for(int i = 0;i < ans.size();++i) ma = (ma + 1LL * (i + 1) * (all - ans[i]) % Mod) % Mod; printf("Case #%d: %lld\n",++ca,ma); } //system("pause"); return 0; } /* 12 14 1 2 1000000000 1 3 1000000000 2 4 1000000000 3 4 1000000000 1 5 1000000000 5 6 1000000000 5 8 1000000000 6 7 1000000000 7 8 1000000000 7 9 1000000000 9 10 1000000000 10 11 1000000000 11 12 1000000000 9 12 1000000000 40 10 10 1 2 2 1 3 4 1 4 3 1 5 6 1 6 22 1 7 31 1 8 12 1 9 12 9 10 24 8 10 7 40 */



