信息安全读书笔记day02-数论基础_素数_模运算_欧几里得算法_费马欧拉定理

今天学习了数论的基础算法以及定理，如素数的定义、模运算、欧几里得算法、费马小定理和欧拉定理。

1、欧几里得算法

欧几里得算法和我国的辗转相除法作用一样，都可以求两个数的最大公约数以及最小公倍数。刷题中经常会遇到这种迭代求解的问题，可以借鉴欧几里得算法的思想。

定义求解 a 和 b 的最大公约数为：gcd(a, b) ，其中 gcd(a, 0)=|a| 。其核心思想是将求解 gcd(a, b) 转换为求解 gcd(b, a mod b) 的值，直到 a mod b 为零时，此时最大公约数就是 b。

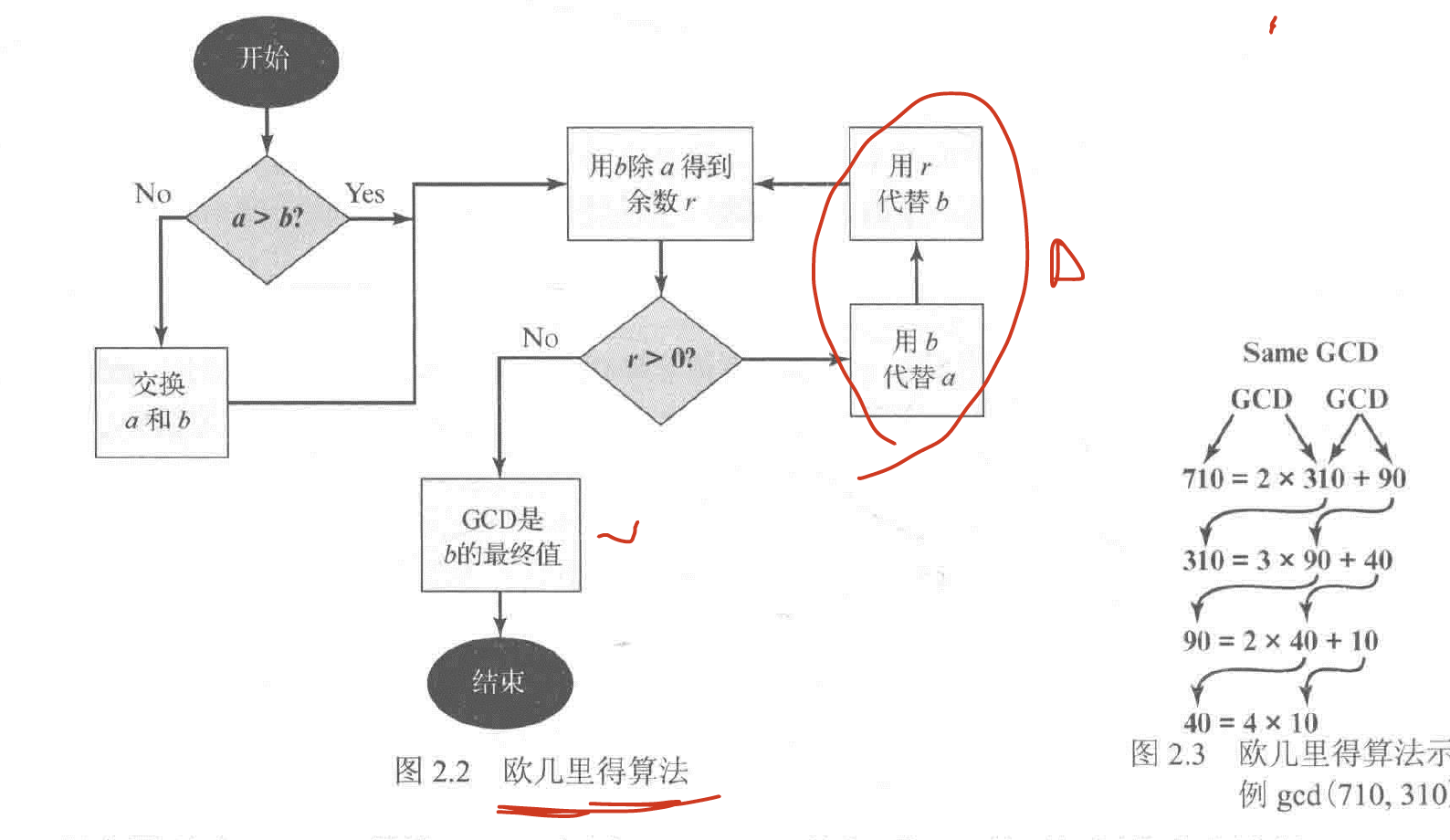
# 使用欧几里得算法计算a和b的最大公约数

def max_part(a, b):
    
    return b if a%b==0 else max_part(b, a%b)

print(max_part(20, 15))  # 5

2、素数

素数又称为质数，定义：一个大于1的自然数，除了1和本身外，不能被其他自然数整除，这样的数称为素数。例如：2、3、5、7等。

任意素数 a 都可以进行因式分解：

\[a = p_1^{a_1}*p_2^{a_2}……*p_i^{a_i} \]

两个数互为素数的概念：若两个数无公共素因子，即它们的公共因子只有1，称为两个数互素。例如：6和15就是互素的。

3、取模定理

（1）模：\(a = qn + r\)，其中正整数 n 称为 a 的模数，若(a mod n)==(b mod n) 则称 a 和 b 是模 n 同余的，表示为\(a\equiv b(mod n)\)

（2）模的算术运算：

(a + b) % n = ((a % n) + (b % n)) % n （1）
(a - b) % n = ((a % n) - (b % n)) % n （2）
(a * b) % n = ((a % n) * (b % n)) % n （3）
a ^ b % n = ((a % n)^n) % n （4）

这个定理很重要，可适用于让你求一个很大的数的后几位。之前刷oj的时候遇到好几个用到此定理的题，比如一个让你求 $2^{120} $的后三位的值，如果不使用取模定理，电脑根本计算不了这么大的数，感受到定理的威力了吧。具体可看我之前写的文章快速幂算法。

总结：

感觉公式有点抽象，比如费马和欧拉定理，要是有应用的例子就好理解了，估计到第三章的各种加密技术会用到，到时再深入理解。