数值计算

 

基于梯度的优化方法

　　目标函数（准则）：需要最小化或者最大化的函数，对其进行最小化时，也称代价函数、损失函数或误差函数。

　　通常使用上标*表示最小化或最大化的x值，如x* = arg min f(x)

　　令f'(x) = 0时得到的点有三种情况，如下各种临界点的例子。

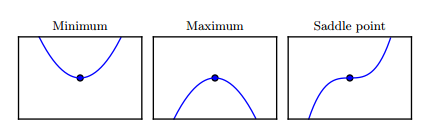
图：临界点的类型。一维情况下，三种临界点的示例，临界点是斜率为零的点。分别是局部极小值，局部极大值和鞍点

　　针对具有多维输入的函数，则利用偏导数。偏导数∂[f(x)]/∂x_i衡量点x处只有x_i增加时f(x)如何变化。梯度是相对一个向量求导的导数：f的导数是包含所有偏导数的向量，记为　▽_xf(x)。梯度的第i个元素是f关于x_i的偏导数。在多维情况下，临界点是梯度中所有元素都为零的点。

　　（链式法则用于复合函数的求导）

　　方向导数是函数f(x+αu)关于α的导数（在α=0时取得），使用链式法则，我们可以看到当α = 0时，∂[f(x+αu)]/∂α = u^T▽_xf(x)

　　为最小化f，应找到使f下降得最快的方向。计算导数：min_u,u^Tu=1 u^T▽_xf(x) = min_u,u^Tu=1 ||u||₂ ||▽_xf(x)||₂cosθ , 其中θ是u与梯度的夹角。将 ||u||₂ =1 代入，并忽略与u无关的项，简化得到 min_u cosθ。这在u与梯度方向上移动可以减少f（被称最速下降法或梯度下降法）。最速下降建议新的点为x' = x - ε▽_xf(x)，其中ε为学习率，是一个确定步长大小的正标量。

　　选择ε的方式：1）直接选择一个小的常数；2）根据几个ε计算f(x - ε▽_xf(x))，并选择其中能产生最小目标函数值的ε(线搜索)。

　　最速下降在梯度的每一个元素为零时收敛（或在实践中，很接近零时）。在某些情况下，也许能够避免运行该迭代算法，并通过解方程▽_xf(x) = 0直接跳到临界点。

 

Jacobian（雅克比）矩阵和Hessian矩阵

　　梯度向量：目标函数f为单变量，是关于自变量向量x = (x₁,x2, ... ,x_n)^T的函数，单变量函数f对向量x求梯度，结果为一个与向量x同维度的向量，称之为梯度向量；

g(x) = ▽f(x) = (∂f/∂x₁,∂f/∂x₂,...,∂f/∂x_n)^T

　　Jacobian（雅克比）矩阵:目标函数f为一个函数向量，f = (f₁(x),f₂(x),..,fm(x))^T,其中，自变量为x=(x₁,x2, ... ,x_n)^T,函数向量f对x求梯度，结果为一个矩阵，行数是f的维数，列数是x的维数，称之为Jacobian矩阵。其每一行都是由相应函数的梯度向量转置构成的。

　　当目标函数为标量函数时，Jacobian矩阵就是梯度向量。

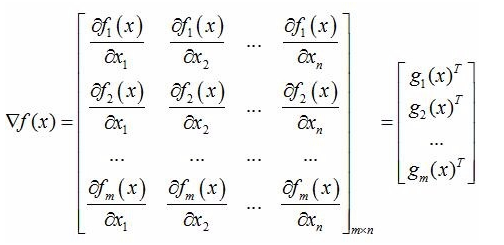
　　Hessian矩阵：实际上，Hessian矩阵是梯度向量g(x)对自变量x的Jacobian矩阵

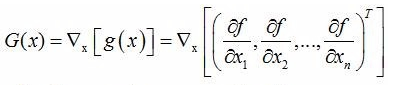
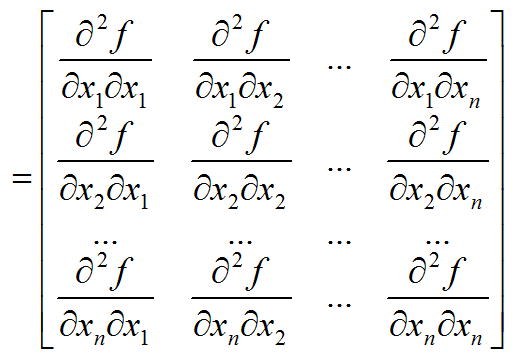
　　 Hessian矩阵在牛顿法中的应用，牛顿法主要应用在两个方面：求方程的根和最优化。

 

约束优化

　　寻找有等式约束条件的函数的最优值得最优化方法

　　(i).无约束优化问题，可写为

min f(x)

　　　　利用费马引理，即函数f(x)在点ξ的某邻域U(ξ)内有定义，并且在ξ处可导，如果对于任意的x∈U（ξ)，都有f(x)≤f(ξ) (或f(x)≥f(ξ))，那么f'（ξ）=0。

　　　　求取f(x)对x的导数，令其为零，求得候选最优值，验证：若为凸函数，则为最优解。

　　(ii). 有等式约束的优化问题，可以写为

min f(x) , s.t. h_i(x) = 0,i = 1,2,...,n

　　　　拉格朗日乘子法：通过拉格朗日系数把等式约束和目标函数组合成L(x,λ) = f(x) + λ×h_i(x) 转化为无约束优化问题

　　(iii). 有不等式约束的优化问题，可写为

min f(x),  s.t.  g_i(x)≤0,i=1,2,...,n; h_j(x) = 0,j = 1,2,...,n

　　　　KKT条件：把所有的不等式约束、等式约束和目标函数全部写成一个式子L(a,b,x) = f(x) + a×g_i(x)+b×h_i(x)

　　　　KKT条件是说最优值必须满足以下条件：

　　　　1）L(a,b,x)对x求导为零

　　　　2) h(x) = 0

　　　　3) a × g(x) = 0 （互补松弛条件）

 

实例：线性最小二乘

　　假设我们希望找到最小化下式的x值：

f(x) = ½ ×||Ax - b||₂²

　　首先计算梯度：

▽_x f(x) = A^T (Ax - b) = A^TAx - A^Tb

　　然后采用小的步长，并按照这个梯度下降。

　　算法：从任意点x开始，使用梯度下降关于x最小化f(x) = ½ ||Ax - b||₂²的算法

　　　　　将步长（ε）和容差（δ）设为小的正数。

　　　　　while  ||A^TAx - A^Tb||₂ > δ   do

　　　　　x ← x - ε(A^TAx - A^Tb)

　　　　　end  while

　　除了梯度下降法，也可以用牛顿法。应为真实函数是二次的，牛顿法所用的二次近似是精确的，该算法会在一步后收敛到全局最小点。

　　现在假设希望最小化同样的函数，但是受x^Tx≤1的约束。引入Lagrangian：

L(x,λ) = f(x) + λ(x^Tx - 1)

　　转换为以下问题：

min_x max_λ≥0 L(x,λ)

　　利用Moore-Penrose伪逆：x=A⁺b 找到无约束最小二乘问题的最小范数解。如果这一点可行，那么这也是约束问题的解。否则，我们必须找到约束是活跃的解。关于x对上述L(x,λ)微分，得到：

A^TAx - A^Tb + 2λx = 0

化得        x = (A^TA+ 2λI)^-1 A^Tb

λ的选择必须使结果服从约束。我们可以关于λ进行梯度上升找到这个值。观察：∂(L(x,λ))/∂λ = x^Tx -1

当范数超过1时，该导数是正的，所以为了跟随导数上坡并相对λ增加Lagrangian，我们需要增加λ。因为x^Tx 的惩罚系数增加了，求解关于x的线性方程现在将得到具有较小范数的解。求解线性方程和调整λ的过程将一直持续到x具有正确的范数并且关于λ的导数是0。