结对项目总结 -- 基于Qt开发的win10桌面应用
担任角色
在这次结对项目中,由于采用了我的个人项目作为参考,所以我继续担任后端开发的角色。
开发环境
前端采用Qt Creator4.13.2 (Community)
后端采用C++
如何复用个人项目
通过对结对项目需求的分析,需要实现的功能大致如下:
-
注册和登录
-
修改密码
-
生成题目
-
题目作答并统计结果
详细功能需求描述和设计框架见下文 “整体设计框架”。
复用的个人项目的工程框架如下
Headers
User.h
SystemPrompt.h
TreeNode.h
RandomizeTestPaper.h
Sources
main.cpp
User.cpp
SystemPrompt.cpp
TreeNode.cpp
RandomizeTestPaper.cpp
通过了解结对项目的功能需求,经过讨论,决定采用以下复用方式
-
复用个人项目中随机生成题目的部分,即 TreeNode 和 RandomizeTestPaper 这两部分。小学题目不需要更改,但初中题目中涉及复杂的平方根运算,高中题目的三角函数也都是与 π 无关的弧度角。当这些情况都合在一起的时候,除了利用库函数计算出小数结果(这样对计算机而言都是可行的,但是对用户的使用体验是极不友好的),难以表示表达式的结果,因此需要对这两个难度的题目进行调整,详见下文“表达式求值”部分。初高的题目调整后,在个人项目的基础上增加 “表达式求值” 功能即可。
-
User 部分与结对项目需求中的 “注册和登录” 有一定的相关度,添加和完善一些功能即可复用。
-
SystemPrompt 部分主要是用于输出一些系统提示,与结对项目需求基本无关,不考虑复用。
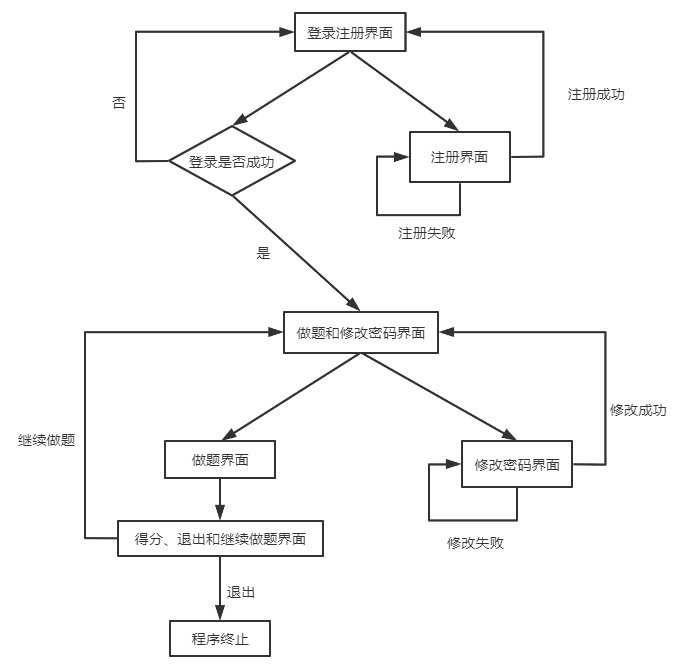
整体设计框架
在清楚如何复用对个人项目的情况下,经过讨论得出结对项目的大致设计框架
表达式求值
添加限制规则的目的:让题目的难度符合正常的小初高试卷难度``
为了避免了平方、开平方、三角函数运算产生的复杂浮点数中间结果对整个表达式求解产生的严重阻碍,我们对小初高运算进行了如下限制:
-
小学表达式不作任何改变。
-
初中表达式中,平方内的运算结果一定在[-100, 100]之间,避免计算大数的平方;开平方内的运算结果一定是[1, 400]之间的平方数,保证开平方的结果是整数。
-
高中表达式中,三角函数全都是与 π 有关的特殊角,计算结果一定是-1, -1/2, 0, 1/2, 1只中的一个。
如此限制,整个表达式的计算结果最多包含一位小数。
构造逆波兰式
问题描述:给出一个名为 infix 的中缀表达式,类型为 string 数组,数组中只包含整数和 "+", "-", "*", "/" , "(", ")". 返回它的逆波兰式,返回类型也是 string 数组。
算法描述:使用一个名为 RPN 的 string 数组存储结果,一个名为 ops 的 string 类型的栈辅助转化,规定 "(" 和 ")".的优先级为 0,"+" 和 "-" 的优先级为 1,"*" 和 "/" 的优先级为 2。
从左至右遍历 infix ,当前位置的字符串记为 str
- 如果 str 是一个数字,直接加入 RPN. 判断下一个 str.
- 否则是操作符,循环执行以下步骤。
- 如果当前栈为空 或 str 是 "(" ,直接入栈,跳出当前循环, 判断下一个 str.
- 否则比较 str 和栈顶操作符的优先级
- 如果 str 的优先级高,直接入栈,跳出当前循环,判断下一个 str.
- 否则 弹出栈顶,非 "(" 的元素全部加入 RPN,直至遇到 "(" 跳出当前循环,判断下一个 str.
遍历完毕后,把 ops 中剩余的元素依次放入 RPN 中即可得到逆波兰式。
参考代码
// 构建逆波兰式
vector<string> RandomizeTestPaper::BuildRPN(string expression)
{
vector<string> infixExpression = BuildInfixExpression(expression); // 中缀表达式
map<string, int> precedence = GetPrecedence(); // 优先级
vector<string> RPN; // 逆波兰式
stack<string> ops; // 用于存储操作符
int infixSize = infixExpression.size();
for (int i = 0; i < infixSize; i++)
{
string s = infixExpression.at(i);
// 是一个数字
if (precedence.find(s) == precedence.end())
{
RPN.push_back(s);
continue;
}
// 是一个操作符
while (true)
{
// 空栈直接入栈
if (ops.empty())
{
ops.push(s);
break;
}
// 左括号 或 优先级比栈顶高 则入栈
map<string, int>::iterator it1 = precedence.find(s);
map<string, int>::iterator it2 = precedence.find(ops.top());
if (s == "(" || (it1->second > it2->second))
{
ops.push(s);
break;
}
// 优先级比栈顶低,要出栈了
string op = ops.top();
ops.pop();
// 左括号作为跳出循环的标志,其他运算符加入 RPN
if (op == "(")
{
break;
}
else
{
RPN.push_back(op);
}
}
}
// 剩余元素加入 RPN
while (!ops.empty())
{
RPN.push_back(ops.top());
ops.pop();
}
return RPN;
}
逆波兰式求值
问题描述:给出一个名为 RPN 的逆波兰表达式,类型为 string 数组,计算这个表达式的结果,返回类型为 int.
算法描述:借助一个名为 stk 的栈,类型为 int.
遍历 RPN 数组,记当前位置的字符串为 str
- 如果 str 是一个数字,直接入栈,判断下一个 str.
- 否则是一个操作符,依次从栈取出两个元素分别作为第二个操作数和第一个操作数,注意先二后一,作当前操作符的运算后,将结果重新入栈,判断下一个 str. 注意除法出现除以 0 要作特殊处理。
参考代码
// 计算逆波兰表达式
int RandomizeTestPaper::calculateRPN(string expression)
{
vector<string> RPN = BuildRPN(expression); // 逆波兰式
stack<int> stk;
int RPNsize = RPN.size();
int operand1 = 0, operand2 = 0;
for (int i = 0; i < RPNsize; i++)
{
if (RPN[i] == "+")
{
operand2 = stk.top();
stk.pop();
operand1 = stk.top();
stk.pop();
stk.push(operand1 + operand2);
}
else if (RPN[i] == "-")
{
operand2 = stk.top();
stk.pop();
operand1 = stk.top();
stk.pop();
stk.push(operand1 - operand2);
}
else if (RPN[i] == "*")
{
operand2 = stk.top();
stk.pop();
operand1 = stk.top();
stk.pop();
stk.push(operand1 * operand2);
}
else if (RPN[i] == "/")
{
operand2 = stk.top();
stk.pop();
operand1 = stk.top();
stk.pop();
if (operand2 == 0)
{
return 0;
}
stk.push(operand1 / operand2);
}
else
{
stk.push(atoi(RPN[i].c_str()));
}
}
int ans = stk.top();
stk.pop();
return ans;
}
运算无效
表达式中出现 "除以0" 或求 "tan(π/2)" 表示运算无效,四个选项中必然包含一个 "无效" 选项。
经验、教训总结
-
注意版本控制。在开发过程中,实现一个功能并反复测试后,可以整合成一个版本。很多时候觉得在添加功能后,导致整个工程编译不通过而且找不出原因,无奈之下只能重新开始慢慢添加功能并反复测试,这非常浪费时间。
-
结对编程尽量面对面交流。开发前期两人讨论完设计框架后就采用线上交流的方式开发,作为后端开发,我提供的接口的功能是正常的,但是参数个数和返回值却不是前端伙伴所需要的,而伙伴在线上也难以清楚具体描述需求,来来回回修改一个又一个版本非常浪费时间。而面对面交流,可以清楚明白伙伴需要什么,迅速开发出相应的接口。
-
帮助伙伴开发。伙伴在开发过程中可以在旁观看,作为旁观者经常能即使发现问题并提醒伙伴修正,不至于让伙伴一个人也许为了一个小问题 debug 很长时间,可以极大提高开发效率。
效果展示
-
登录注册界面

-
做题界面