11、B-树（B树）

一、介绍　

　　二叉查找树、平衡二叉树、红黑树、B树、B+树。前面三种是典型的二叉查找树，查找的时间复杂度是O(log2N)与树的深度有关系，那么降低树的深度也就可以提升查找效率。这时就提出了平衡多路查找树，也就是B树以及B+树。

二、使用场景

　　（1）关系型数据库的索引(MySQL)。

　　（2）计算机磁盘存取文件。

三、B-树的性质

一颗M阶B树T，满足以下条件

　　1. 每个结点至多拥有M棵子树

　　2. 根结点至少拥有两棵子树

　　3. 除了根结点以外，其余每个分支结点至少拥有M/2课子树

　　4. 所有的叶结点都在同一层上

　　5. 有k棵子树的分支结点则存在k-1个关键字，关键字按照递增顺序进行排序（k为一个节点的子节点真实个数）

　　6. 关键字数量满足ceil(M/2)-1 <= n <= M-1

 

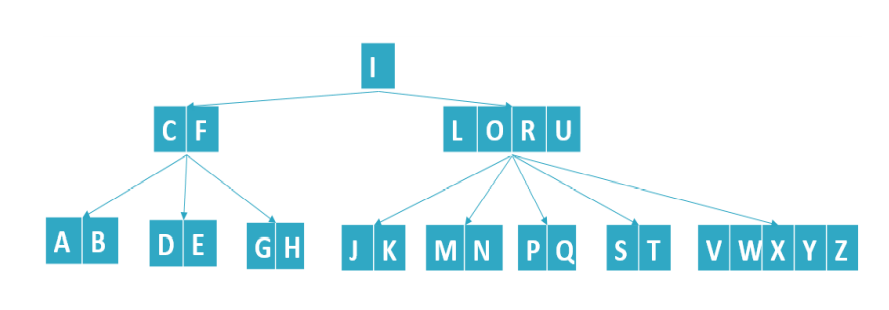
 如上图，为5阶B树，它一个节点中可能存在多个key，例如根节点I的右子节点，存在4个key(L、O、R、U)，

四、B-树添加节点

　　在添加key的时候，存在2中情况：

　　（1）只有根节点，1个节点分裂为3个节点，然后再添加key，如下：

　　　　　　　　

　　（2）其余情况，1分为2节点，如下：

　　　　　　

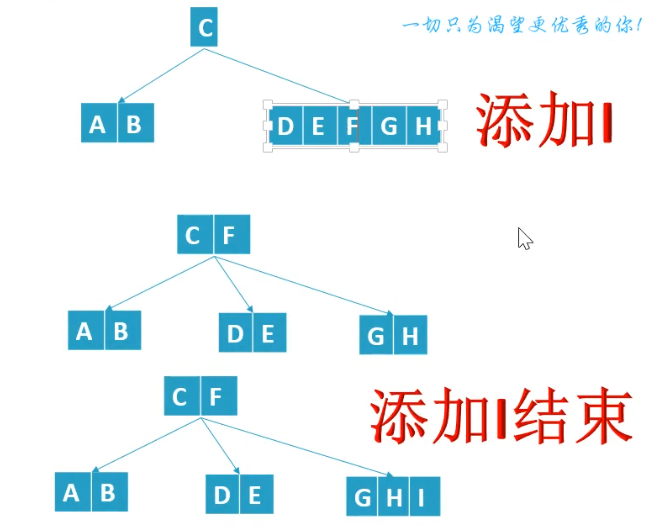
五、代码部分：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#include <assert.h>

#define DEGREE        3
typedef int KEY_VALUE;

typedef struct _btree_node {
    KEY_VALUE *keys;
    struct _btree_node **childrens;
    int num;
    int leaf;
} btree_node;

typedef struct _btree {
    btree_node *root;
    int t;
} btree;

btree_node *btree_create_node(int t, int leaf) {

    btree_node *node = (btree_node*)calloc(1, sizeof(btree_node));
    if (node == NULL) assert(0);

    node->leaf = leaf;
    node->keys = (KEY_VALUE*)calloc(1, (2*t-1)*sizeof(KEY_VALUE));
    node->childrens = (btree_node**)calloc(1, (2*t) * sizeof(btree_node));
    node->num = 0;

    return node;
}

void btree_destroy_node(btree_node *node) {

    assert(node);

    free(node->childrens);
    free(node->keys);
    free(node);
    
}


void btree_create(btree *T, int t) {
    T->t = t;
    
    btree_node *x = btree_create_node(t, 1);
    T->root = x;
    
}

//x为要插入节点位置的父节点，i为父节点的第几个自己点
void btree_split_child(btree *T, btree_node *x, int i) {
    int t = T->t;

    btree_node *y = x->childrens[i];
    btree_node *z = btree_create_node(t, y->leaf);

    z->num = t - 1;


    int j = 0;
    for (j = 0;j < t-1;j ++) {
        z->keys[j] = y->keys[j+t];
    }
    if (y->leaf == 0) {
        for (j = 0;j < t;j ++) {
            z->childrens[j] = y->childrens[j+t];
        }
    }

    y->num = t - 1;
    for (j = x->num;j >= i+1;j --) {
        x->childrens[j+1] = x->childrens[j];
    }

    x->childrens[i+1] = z;

    for (j = x->num-1;j >= i;j --) {
        x->keys[j+1] = x->keys[j];
    }
    x->keys[i] = y->keys[t-1];
    x->num += 1;
    
}

void btree_insert_nonfull(btree *T, btree_node *x, KEY_VALUE k) {

    int i = x->num - 1;

    if (x->leaf == 1) {
        
        while (i >= 0 && x->keys[i] > k) {
            x->keys[i+1] = x->keys[i];
            i --;
        }
        x->keys[i+1] = k;
        x->num += 1;
        
    } else {
        while (i >= 0 && x->keys[i] > k) i --;

        if (x->childrens[i+1]->num == (2*(T->t))-1) {
            btree_split_child(T, x, i+1);
            if (k > x->keys[i+1]) i++;
        }

        btree_insert_nonfull(T, x->childrens[i+1], k);
    }
}

void btree_insert(btree *T, KEY_VALUE key) {
    //int t = T->t;

    btree_node *r = T->root;
    if (r->num == 2 * T->t - 1) {
        
        btree_node *node = btree_create_node(T->t, 0);
        T->root = node;

        node->childrens[0] = r;

        btree_split_child(T, node, 0);

        int i = 0;
        if (node->keys[0] < key) i++;
        btree_insert_nonfull(T, node->childrens[i], key);
        
    } else {
        btree_insert_nonfull(T, r, key);
    }
}

void btree_traverse(btree_node *x) {
    int i = 0;

    for (i = 0;i < x->num;i ++) {
        if (x->leaf == 0) 
            btree_traverse(x->childrens[i]);
        printf("%C ", x->keys[i]);
    }

    if (x->leaf == 0) btree_traverse(x->childrens[i]);
}

void btree_print(btree *T, btree_node *node, int layer)
{
    btree_node* p = node;
    int i;
    if(p){
        printf("\nlayer = %d keynum = %d is_leaf = %d\n", layer, p->num, p->leaf);
        for(i = 0; i < node->num; i++)
            printf("%c ", p->keys[i]);
        printf("\n");
#if 0
        printf("%p\n", p);
        for(i = 0; i <= 2 * T->t; i++)
            printf("%p ", p->childrens[i]);
        printf("\n");
#endif
        layer++;
        for(i = 0; i <= p->num; i++)
            if(p->childrens[i])
                btree_print(T, p->childrens[i], layer);
    }
    else printf("the tree is empty\n");
}


int btree_bin_search(btree_node *node, int low, int high, KEY_VALUE key) {
    int mid;
    if (low > high || low < 0 || high < 0) {
        return -1;
    }

    while (low <= high) {
        mid = (low + high) / 2;
        if (key > node->keys[mid]) {
            low = mid + 1;
        } else {
            high = mid - 1;
        }
    }

    return low;
}


//{child[idx], key[idx], child[idx+1]} 
void btree_merge(btree *T, btree_node *node, int idx) {

    btree_node *left = node->childrens[idx];
    btree_node *right = node->childrens[idx+1];

    int i = 0;

    /////data merge
    left->keys[T->t-1] = node->keys[idx];
    for (i = 0;i < T->t-1;i ++) {
        left->keys[T->t+i] = right->keys[i];
    }
    if (!left->leaf) {
        for (i = 0;i < T->t;i ++) {
            left->childrens[T->t+i] = right->childrens[i];
        }
    }
    left->num += T->t;

    //destroy right
    btree_destroy_node(right);

    //node 
    for (i = idx+1;i < node->num;i ++) {
        node->keys[i-1] = node->keys[i];
        node->childrens[i] = node->childrens[i+1];
    }
    node->childrens[i+1] = NULL;
    node->num -= 1;

    if (node->num == 0) {
        T->root = left;
        btree_destroy_node(node);
    }
}

void btree_delete_key(btree *T, btree_node *node, KEY_VALUE key) {

    if (node == NULL) return ;

    int idx = 0, i;

    while (idx < node->num && key > node->keys[idx]) {
        idx ++;
    }

    if (idx < node->num && key == node->keys[idx]) {

        if (node->leaf) {
            
            for (i = idx;i < node->num-1;i ++) {
                node->keys[i] = node->keys[i+1];
            }

            node->keys[node->num - 1] = 0;
            node->num--;
            
            if (node->num == 0) { //root
                free(node);
                T->root = NULL;
            }

            return ;
        } else if (node->childrens[idx]->num >= T->t) {

            btree_node *left = node->childrens[idx];
            node->keys[idx] = left->keys[left->num - 1];

            btree_delete_key(T, left, left->keys[left->num - 1]);
            
        } else if (node->childrens[idx+1]->num >= T->t) {

            btree_node *right = node->childrens[idx+1];
            node->keys[idx] = right->keys[0];

            btree_delete_key(T, right, right->keys[0]);
            
        } else {

            btree_merge(T, node, idx);
            btree_delete_key(T, node->childrens[idx], key);
            
        }
        
    } else {

        btree_node *child = node->childrens[idx];
        if (child == NULL) {
            printf("Cannot del key = %d\n", key);
            return ;
        }

        if (child->num == T->t - 1) {

            btree_node *left = NULL;
            btree_node *right = NULL;
            if (idx - 1 >= 0)
                left = node->childrens[idx-1];
            if (idx + 1 <= node->num) 
                right = node->childrens[idx+1];

            if ((left && left->num >= T->t) ||
                (right && right->num >= T->t)) {

                int richR = 0;
                if (right) richR = 1;
                if (left && right) richR = (right->num > left->num) ? 1 : 0;

                if (right && right->num >= T->t && richR) { //borrow from next
                    child->keys[child->num] = node->keys[idx];
                    child->childrens[child->num+1] = right->childrens[0];
                    child->num ++;

                    node->keys[idx] = right->keys[0];
                    for (i = 0;i < right->num - 1;i ++) {
                        right->keys[i] = right->keys[i+1];
                        right->childrens[i] = right->childrens[i+1];
                    }

                    right->keys[right->num-1] = 0;
                    right->childrens[right->num-1] = right->childrens[right->num];
                    right->childrens[right->num] = NULL;
                    right->num --;
                    
                } else { //borrow from prev

                    for (i = child->num;i > 0;i --) {
                        child->keys[i] = child->keys[i-1];
                        child->childrens[i+1] = child->childrens[i];
                    }

                    child->childrens[1] = child->childrens[0];
                    child->childrens[0] = left->childrens[left->num];
                    child->keys[0] = node->keys[idx-1];
                    
                    child->num ++;

                    node->keys[idx-1] = left->keys[left->num-1];
                    left->keys[left->num-1] = 0;
                    left->childrens[left->num] = NULL;
                    left->num --;
                }

            } else if ((!left || (left->num == T->t - 1))
                && (!right || (right->num == T->t - 1))) {

                if (left && left->num == T->t - 1) {
                    btree_merge(T, node, idx-1);                    
                    child = left;
                } else if (right && right->num == T->t - 1) {
                    btree_merge(T, node, idx);
                }
            }
        }

        btree_delete_key(T, child, key);
    }
    
}


int btree_delete(btree *T, KEY_VALUE key) {
    if (!T->root) return -1;

    btree_delete_key(T, T->root, key);
    return 0;
}


int main() {
    btree T = {0};

    btree_create(&T, 3);
    srand(48);

    int i = 0;
    char key[26] = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
    for (i = 0;i < 26;i ++) {
        //key[i] = rand() % 1000;
        printf("%c ", key[i]);
        btree_insert(&T, key[i]);
    }

    btree_print(&T, T.root, 0);

    for (i = 0;i < 26;i ++) {
        printf("\n---------------------------------\n");
        btree_delete(&T, key[25-i]);
        //btree_traverse(T.root);
        btree_print(&T, T.root, 0);
    }
    
}