一、无穷级数
我们在上册中已经学过泰勒公式,知道在一定条件下,一个函数可以用多项式近似表示,多项式的次数越高精确程度也就越高,但是要用多项式精确表示一个函数是做不到的,这就启发我们去研究这样一个问题：是否有可能用无限多项幂函数的和来精确表示函数，另外，在数学和实际问题中碰到的很多值,如e,sin13°,In3等很难计算,如果能将这类值精确地表示成无限多个容易计算的有理数的和,那么求出这类值的近似值就不那么困难了.这些“无限项”求和的问题涉及微积分中的一个重要的内容----无穷级数
1、无穷级数的概念
设有数列
µ1,µ2,···,µn,···, (11.1.1)
对数列(11.1.1),的各项依次用加号连接起来的表达式
µ1 + µ2 + ··· + µn + ··· (11.1.2)
称为常数项无穷级数,简称数项级数或级数、其中µn称为级数(11.1.2)的一般项(或通项).(11.1.2)也可写成
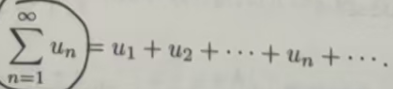
应该注意,无穷级数中的无限个数相加只是形式上的,因为无限相加与有限相加本质上是有差别的,有限相加的和总是存在的,而无限相加是否一定有“和”还不知道,即使有“和”,和是什么?这些就构成了无穷级数的基本问题.
如级数1-1+1-1+1+…,若加括号(1-1)+(1-1)+(1-1)+…, 则其和为0;换一种方法加括号1-(1-1)-(1-1)+…,则其和为1.
为了简单书写，下面所有的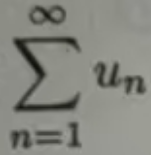
用 Σµn 表示，
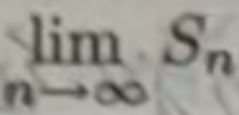用limSn表示
为了搞清楚这些问题,先从有限和着手,考虑级数Σµn 前面有限项的和:
S1=µ1,
S2=µ1 + µ2,
....
Sn=µ1 + µ2 +··· + µn,
称数列{S„}为级数Σµn 的部分和数列, 称第n项Sn=µ1 + µ2 +··· + µn,为级数Σµn 的前n项部分和.
定义 11.1.1 如果级数 Σµn 的部分和数列 {Sn}有极限,即
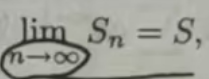
则称级数 Σµn 收敛，并称S为级数 Σµn 的和,记作
如果{Sn}没有极限,则称级数 Σµn 发散.
根据定义,级数 Σµn 是否有和(是否收敛)的问题转化为部分和数列{Sn}是否收敛的问题
例 11.1.1 证明几何级数a+aq+aq2 +…+aqn-1 +…(a≠0) 当|q| < 1时收敛，|q| ≥1 时发散
证 |q|≠1时,级数的部分和为
Sn=a+aq+aq2 +…+aqn-1 = a(1-qn)/(1-q)
所以,当|ql<1时,有
(由于0<q<1,当n → ∞时，指数函数递减qn →0), 原级数收敛,其和为S=a/(1-q)
当|ql>1时,有
(由于q>1,当n → ∞时，指数函数递增qn →∞),原级数发散
q=1时,级数为a + a + a + ··· + a + ···,它的部分和Sn=na，limSn = ∞,所以级数发散.
q=-1时,级数为a - a + a - ··· + a + ···,于是 S2n =0,S2n+1=a.因此{S„}没有极限,所以级数也发散,
例 11.1.2 证明级数收敛,并求和
证
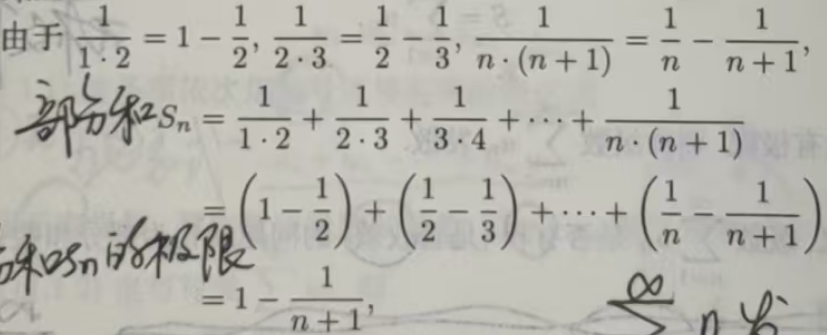
所以 lim Sn=1.因此级数收敛,其和为 1.
例11.1.3 证明级数1+2+3+·…+n+···=Σn 发散
证因为Sn=1+2+3+···+n = n(n+1)/2,所以lim Sn = +∞，,从而级数Σn 发散
例11.1.4证明级数 是发散的(这个级数称为调和级数)
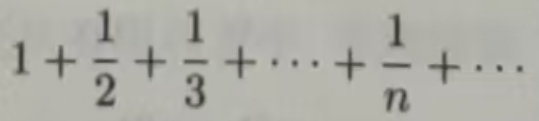
证 这个级数的一般项µn = 1/n可以用一个积分表示:
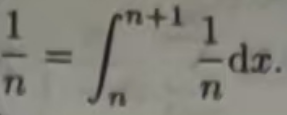
当n≤x≤n+1时,有1/n≥1/x,所以(∫1/xdx=ln|x|+C;)
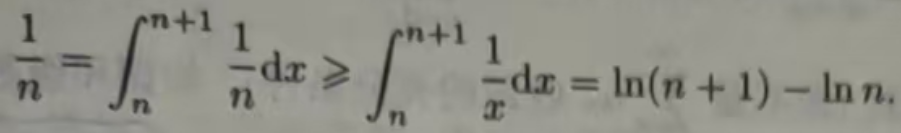
于是
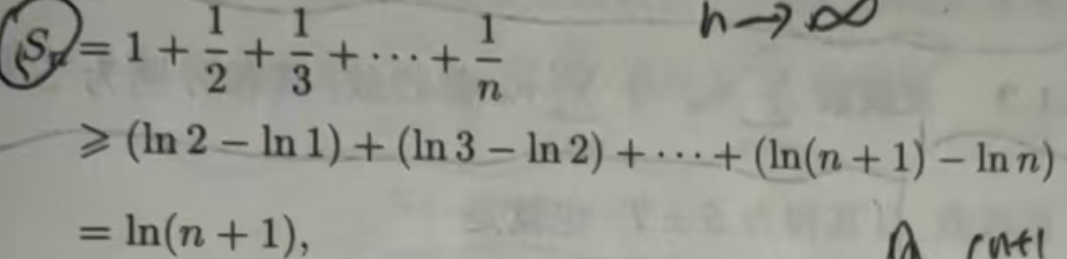
因此 lim Sn= +∞,从而调和级数发散.
2、收敛级数的性质
上面用级数的定义对几个级数的收敛性进行了判断.一般来说,要用limSn是否存在来判断级数是否收敛是困难的,需要对级数的收敛性建立一些基于级数本身性质的判断法.首先引进收敛级数的一些性质,利用这些性质可以判断一些级数的收敛或发散(敛散性)
定理 11.1.1(级数收敛的必要条件) 如果级数Σµn 收敛，则n→∞时,limµn =0，即收敛级数的一般项收敛于0.
证设级数Σµn 收敛于和S;则其部分和数列{Sn}也收敛于 S，由于µn =Sn -Sn-1,所以
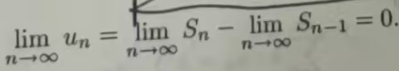
定理11.1.1说明级数Σµn 的一般项µn 收敛于0是该级数收敛的必要条件.也就是如果n→∞时,limµn ≠0,则级数Σµn 一定发散,如上面的例 11.1.3.
例 11.1.5 讨论级数Σn/(2n+1) 的敛散性.
解 因为
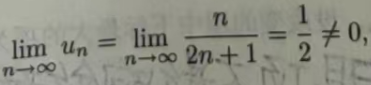
所以级数Σn/(2n+1) 发散
值得注意的是n→∞时,limµn =0只是级数Σµn 收敛的必要条件,n→∞时,limµn =0并不能保证 Σµn 收敛 (即不是Σµn 收敛的充分条件).如调和级数(11.1.3)的一般项µn =1/n 趋于 0,但不收敛.
定理11.1.2 设级数Σµn 和Σνn 都收敛,其和分别为S与T,则级数Σ(µn ±νn ) 也收敛,且其和为S±T.也就是
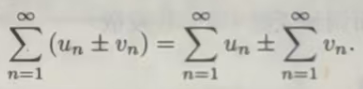
定理 11.1.3 如果级数Σµn 收敛,其和为 S,k是任一常数,则级数Σkµn 也收敛,且其和为 kS,即
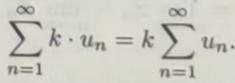
推论 级数Σµn 与Σkµn (k是不为0的常数)有相同的敛散性
定理11.1.4 增加、去掉或改变级数的有限项不影响该级数的敛散性
定理11.1.5 如果级数Σµn 收敛,则对该级数的项任意加括号后得到的级数仍然收敛,且和不变
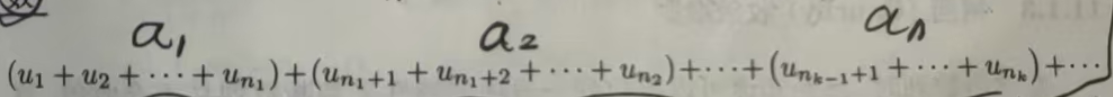
注 加括号后的级数收敛,不能得出原级数收敛,这与数列的一个子列收敛不能得出该数列收敛的理由是一样的.如级数(1-1)+(1-1)+·…收敛于 0,去掉括号后的级数1-1+1-1+..·发散.
根据数列的性质,如果数列的某个子列发散,那么该数列也发散,可以推得如果加了括号后的级数发散,那么原级数一定发散.
最后,再讨论级数与数列的关系、由前面讨论知道可以由级数Σµn 得到部分和数列{Sn},并且级数的敛散性由部分和数列确定；反之，对任一数列{an }，如果令
（即由数列得到级数）
则级数Σµn = a1+(a2- a1)+···+(an-an-1)+…·与数列{an}有相同的敛散性,且收敛时有
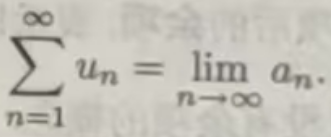
数列与级数的这种关系,对我们理解级数的敛散性很有帮助.
3、柯西(Cauchy)收敛准则
在学习数列时,已经知道可以用数列一般项的特性来判断数列是否会收敛,这就是柯西收敛判断准则,根据数列与级数的关系,同样,可以对级数建立柯西准则.
定理11.16(柯西准则 级数Σµn 收敛的充分必要条件是对于任意给定的ε>0,存在N∈N,使当n>N时,对一切自然数p,都有
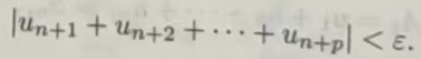
4、正项级数的收敛准则
如果级数Σµn 的每一项都是非负实数(即µn ≥0,n=1,2,…),则称该级数为正项级数
对于每一项都是非正的级数,可以用(-1)乘以每一项而得到正项级数,这类级数的敛散性可以化为正项级数来讨论.由于正项级数比较简单,也容易讨论,首先建立一个有关正项级数收敛性的判别准则,然后再建立一些判别级数敛散性的方法.
定理11.2.1 正级数Σµn 收敛的充分必要条件是其部分和数列{Sn} 有界
证 由于Σµn 是正项级数,它的部分和数列{Sn}满足 Sn+1= Sn+un+1 > Sn, 所以{Sn}是单调增加数列.
必要性 Σµn 收敛,则{Sn}也收敛,从而{Sn}有界.
充分性 由于{Sn}是单调增加数列,如果{Sn}有界,则根据数列单调有界准则,知{Sn}收敛,也就是 Σµn 收敛.
例11.2.1 证明p级数
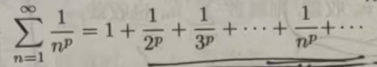
当p≤1时发散,p>1时收敛.
证 当p≤1时,
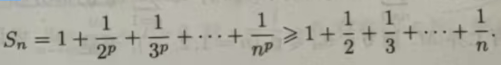
上式右边是调和级数的部分和,它发散到正无穷大,因此p级数也发散到正无穷大.
当p>1时,有xp≤np,(n-1≤x≤n),于是
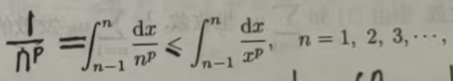
从而
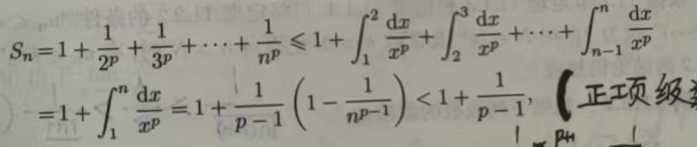
即{Sn}有上界.因此当p>1时,p级数收敛
由例 11.2.1可知,
级数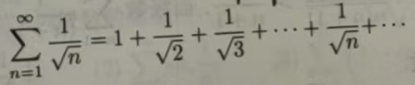
发散,
级数
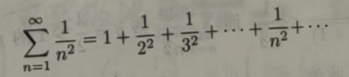收敛
5、比较判别法
当了解了正项级数的收敛准则及有了若干敛散性已知的级数,就可以建立以下比较判别法.
定理 11.2.2设级数Σµn 和Σvn 都是正项级数 且µn ≤vn ，(n=1,2,....)
(1)如果级数Σvn 收敛，则级数Σµn 也收敛;
(2)如果级数Σµn 发散，则级数Σvn 也发散.
注使用比较判别法的关键是要找到敛散性已知可以比较的级数,如p级数、几何级数
推论 (比较判别法的极限形式) 设Σµn 、Σvn 都是正项级数,且vn ≠0. 如果n→∞时，limµn / vn = l,则
(i) 当0<l<+∞时，Σµn 、Σvn 有相同的敛散性;
(ii) 当l=0时，Σvn 收敛时，Σµn 也收敛;
(iii) 当l=+∞时且Σvn 发散时，Σµn 也发散;
例11.2.3判别下列级数的敛散性:
解 因为
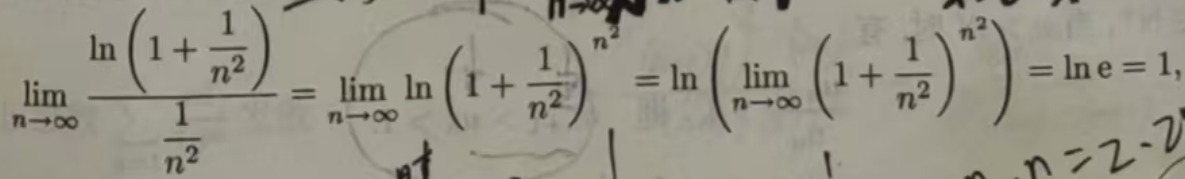
两个重要极限
6、比式判别法和根式判别法
使用比较判别法的困难是要找到一个可供比较的已知敛散性的级数,从使用的角度讲,能根据级数一般项本身的性质直接判定级数是否收敛比较方便.
定理 11.2.3(比式判别法)设Σµn 为正项级数,如果
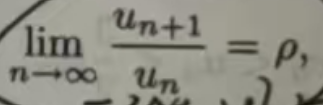则当ρ<1时,级数收敛;当ρ>1(或ρ=+∞) 时,级数发散
比式判别法也称为达朗贝尔(d’Alembert)判别法
特别注意,当ρ=1时,比式判别法无法确定级数Σµn 的敛散性,但是如果存在N,当 n>N 时,有µn+1 /µn≥1,则级数Σµn 发散(请读者自己证明).
由于比式判别法的实质是与几何级数进行比较,而几何级数的一般项收敛速度比较快,所以当被考察的级数收敛速度较慢时,比式判别法就失效了,如p级数对任何p>0都有
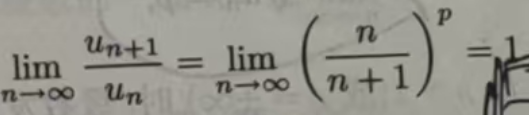
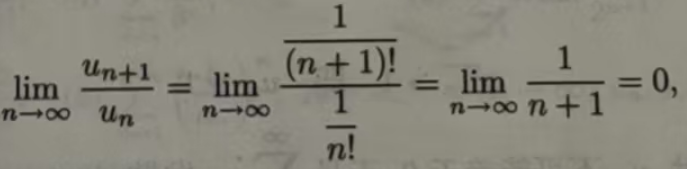
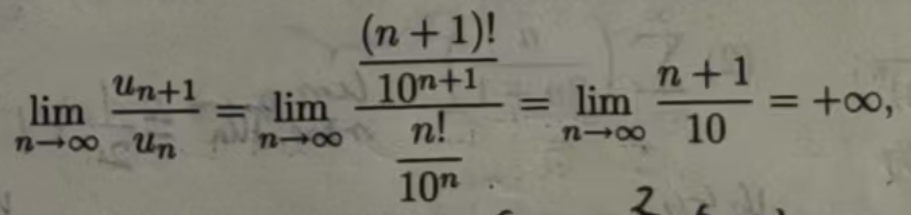
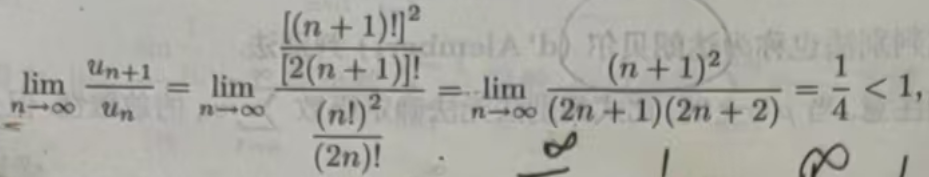
定理 11.2.4(根式判别法)设Σµn 是正项级数,如果
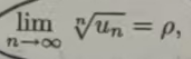则当ρ<1时,级數收敛:当ρ>1(或ρ=+∞)时,级数发散。
根式判别法也秋为柯西判别法
与比式判别法一样,当ρ=1时,根式判别法无法判别级数的敛散性,
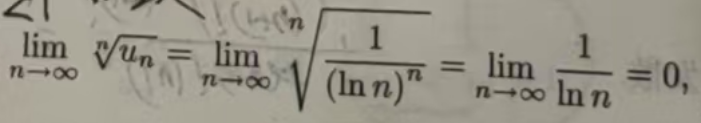
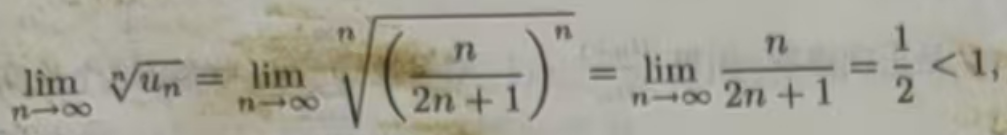
比较例11.2.4与例11.2.5中的例子,不难找到使用比式和根式判别法的级数类型.另外,在通常情况下,级数发散其一般项也可以趋于0.但如果用比式或根式判别法判定级数发散时,该级数的一般项一定不趋于0,而这个性质在判别非正项级数时将起重要作用.
二、傅里叶级数
在前面讨论函数的幂级数展开时知道,一个函数能够展开成幂级数要求是很高的,如任意阶可导,余项随n增大趋于零等,如果函数没有这么好的性质,我们还是希望能够用一些熟知的函数组成的级数来表示该函数,这就是本节要讨论的傅里叶级数,即将一个周期函数展开成三角函数级数.傅里叶级数在物理学中有非常重要的应用.
1、三角级数,三角函数系的正交性
在物理学中常常要研究一些非正弦函数的周期函数,如电子技术中常用矩形波,反映的是一种复杂的周期运动.下面讨论复杂的周期函数在什么情况下能展开成三角函数组成的级数(简称三角级数).
三角级数的一般形式是：
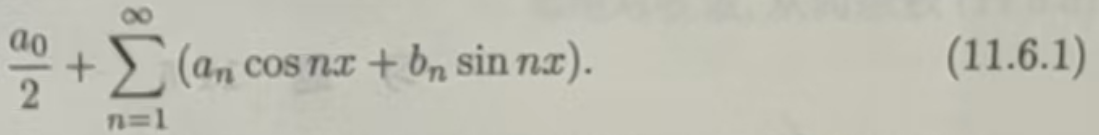
显然,如果三角级数(11.6.1)收敛,其和函数也是周期函数,反过来,一个周期函数f(x)是否能展开成三角级数?如果能够展开成三角级数,如何由f(x)确定系数an,bn,这些系数确定后,三角级数是否一定都收敛于f(x)呢?下面我们来一-解决这些问题.1
首先介绍三角函数系的正交性.
三角函数系
1=cos0x，故三角函数系的集合就是cosnx和sinnx的组合，其中n=0,1,2,3,....
正交性
有两个重要的性质:
(1)每一个函数自身平方在长度为2π的区间上的积分为正;
(2)任何两个不同函数的乘积在长度为2π的区间上积分为零
具有这两个性质的函数系通常称为在所述区间上具有正交性
两个函数正交
在二维平面空间内，如果向量a=（2，1）和向量b=（-1，2）垂直，内积a•b = |a|*|b|cosφ = 0，a•b =（2，1）*（-1，2）=0
如果向量a=（1，2，5）和向量b=（1，2，-1）垂直，内积a•b =1*1+2*2-5*1=0
如果向量a=（a1 ，a2 ，...，an ）和向量b=（b1 ，b2 ，...，bn ）垂直，内积a•b =a1 *b1 +a2 *b2 + ...+ an *bn = Σai *bi =0
如果两个函数f(x)和g(x)的内积为零，即∫ f(x)g(x)dx=0，则称这两个函数相互正交。
证明三角函数系正交
不失一般性,在区间[-π,π]上对三角函数系验证上述两个性质。我们从三角函数系中任选两个函数，来证明这两个函数是正交的。
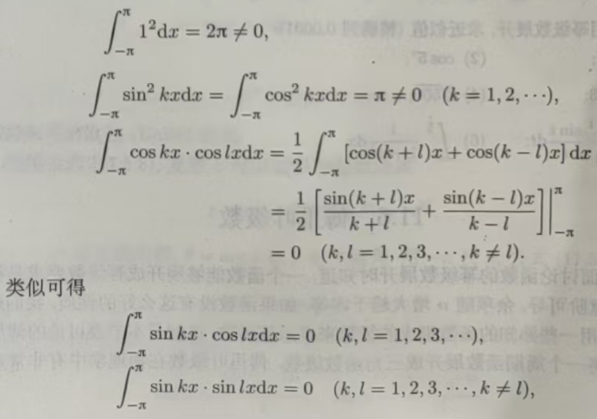
所以三角函数系(11.6.2)是正交的.
2、周期为 2π的函数的傅里叶级数
周期为2π，即f(x) = f(x+2π)
（1）、设f(x)是周期为2π的周期函数,且能展开成三角级数:
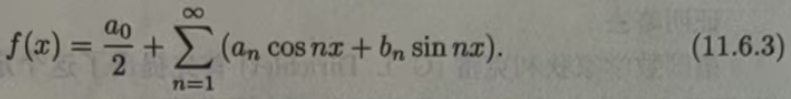
还可以写成如下的形式：
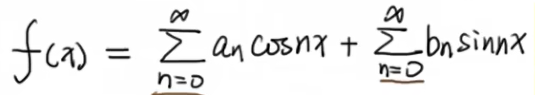
那为什么(11.6.3)中有a0/2呢？
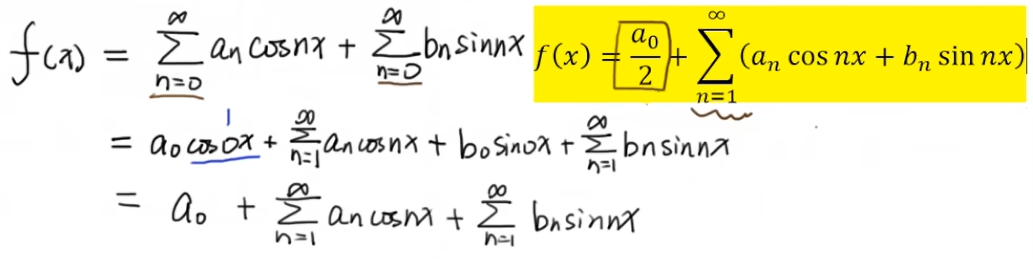
我们发现这里是a0，而上面是a0/2，现在我们来求a0，大家就明白了。
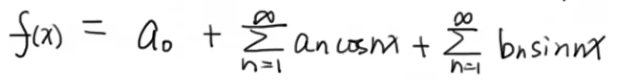
我们对上面等式的左右两边分别从[-π,π]进行积分
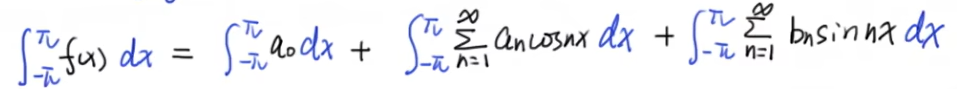
由于cosnx= 1*cosnx，即两个三角函数系中的函数相乘，并在[-π,π]进行积分，由于三角函数系的正交性，故上式右边第二项一定等于0
由于sinnx= 1* sinnx，即两个三角函数系中的函数相乘，并在[-π,π]进行积分，由于三角函数系的正交性，故上式右边第三项一定等于0
故：
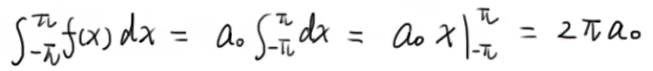
如果傅里叶级数为(11.6.3)时，系数a0的值如下：
所以上面两种写法都是可以的，唯一的区别就是a0的值有区别。
（2）、如果三角级数(11.6.3)可以逐项积分,于是有
对上面等式的左右两边分别从[-π,π]进行积分
根据三角函数系的正交性及cosnx= 1*cosnx和sinnx= 1* sinnx，所以上式右边第二项一定为0，所以
（3）、用cosnx乘(11.6.1)式两端,再从-π到π逐项积分可得
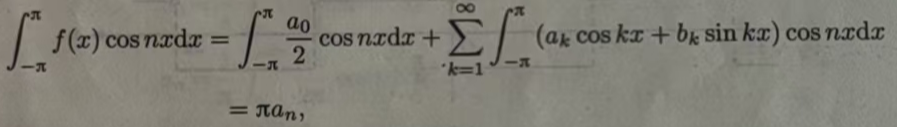
由于cosnx= 1*cosnx，根据三角函数系的正交性，右边第一项为0。对于右边第三项，sinkx与cosnx在任何时候在长度为2π的区间上积分为零
对于右边第二项，k是变量，n是定值，coskx与cosnx只有当n=k时，值才不为零，为anπ，所以右边第二项为anπ
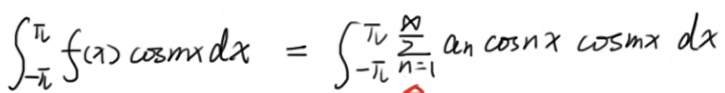
右边只有当m=n时，右边的值才不为零，所以
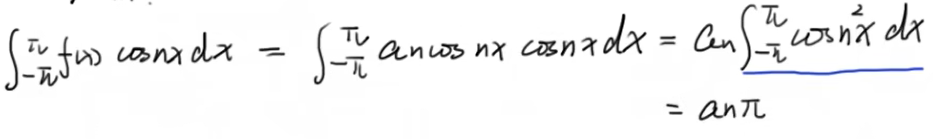
所以系数an为
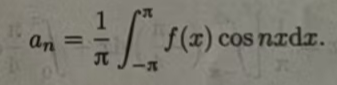
（4）、用sinnx乘(11.6.1)式两端,再从-π到π逐项积分可得
系数bn为
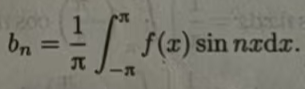
公式(11.6.4)可以看作公式(11.6.5)当n=0时的特殊情形.
由公式(11.6.4)~(11.6.6)所确定的实数 an,bn称为函数f(x)的傅里叶系数.将这些系数代入(11.6.3)式右端所得的三角级数称为函数f(x)的傅里叶级数,记作
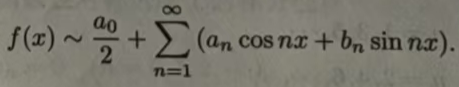
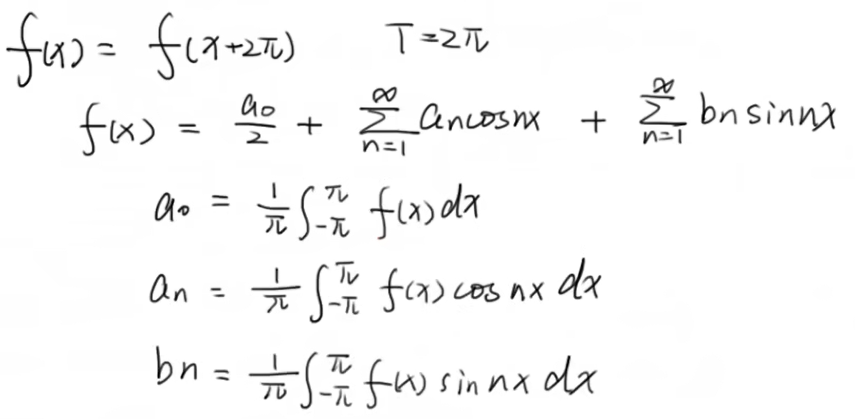
以上的计算过程中有很多假定,首先假定所给函数可以展开成三角级数,其次假定级数可以逐项积分,但这些假定是否合理现在尚且不知,是我们要解决的重要的问题.下面定理给出了这个问题的一个重要结论.
定理 11.6.1(收敛定理)设以2π为周期的函数f(x)在区间[-π,π]上满足下列条件:
(1)连续或只有有限个第一类间断点;
(2)最多只有有限个极值点.
则 f(x)的傅里叶级数收敛,而且当x是f(x)的连续点时,级数收敛于f(x);当是 f(x)的间断点时,级数收敛于 [f(x-0)+ f(x + 0)]/2.
f(x+0)和f(x-0)应该是指右极限和左极限
证明略去.
德国数学家狄利克雷(G.L.Dirichlet)首先提出了这个定理并给出了严格的证明,因此定理中所述的条件常称为狄利克雷条件.
例11.6.1设f(x)是周期为2π的周期函数,其在[-π,π]上的表达式为(图11.1) 试将f()展开成傅里叶级数.
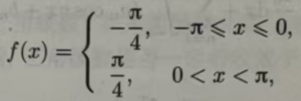
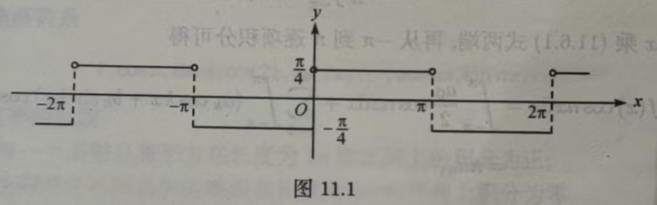
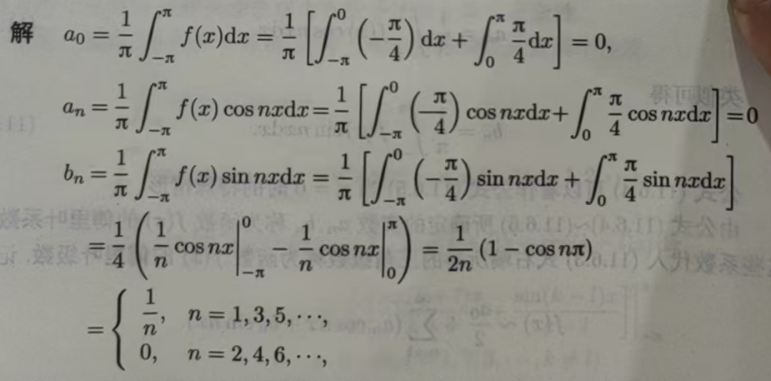
由于∫cosxdx=sinx+C，所以∫cosnxdnx=sinnx+C;另外sinnπ=0
故
根据收敛定理,知f(x)的傅里叶级数在x≠ kπ(k=0,±1,…)处收敛于 f(x),在x=kπ(k=0,±1,··)处,收敛于 0.
例11.6.2 将示波器、电视和雷达中扫描用的周期为2π的锯齿波的波形函数(图11.2)展开成傅里叶级数.
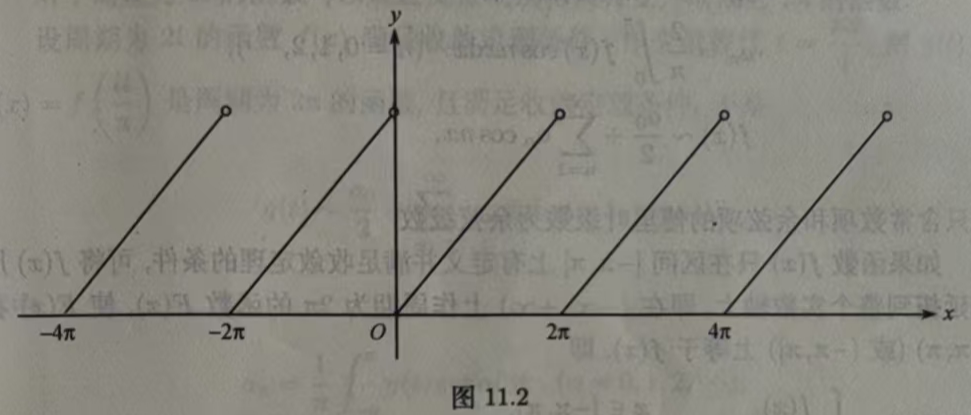
解 锯齿波函数在(0,2π)内的表达式为f(x)=Ax/2π,所以
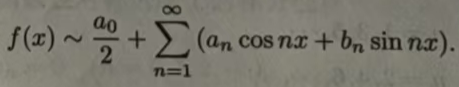
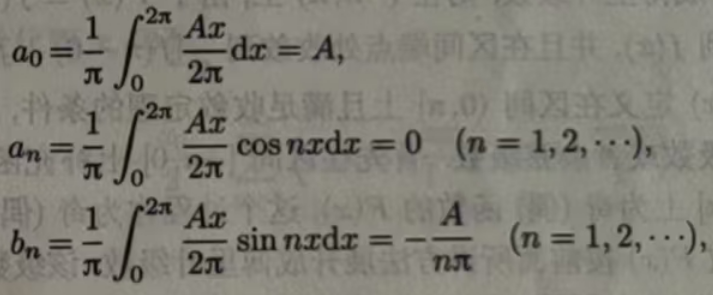
故
根据收敛定理,当x≠2kπ(k为整数)时,f(x)的傅里叶级数收敛于f(x);当=2kπ(k 为整数)时,收敛于A/2
1、如果周期为2π的函数f(x)是奇函数,
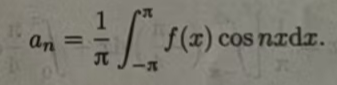
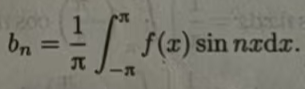
那么f(x)cosnx 是奇函数,f(x)sinnx是偶函数.根据奇、偶函数在对称区间上的积分性质可知,此时傅里叶系数为
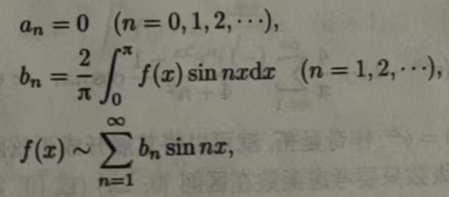
我们将只含正弦项的傅里叶级数称为正弦级数
2、同样,当周期为2π的函数f(x)是偶函数时,
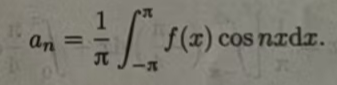
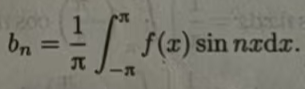
那么f(x)cosnx 是偶函数,f(x)sinnx是奇函数.根据奇、偶函数在对称区间上的积分性质可知,此时傅里叶系数为
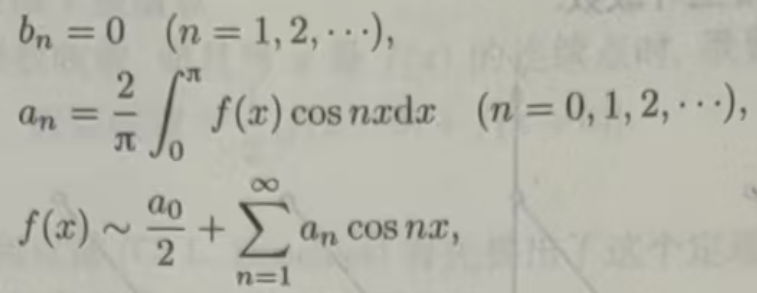
称只含常数项和余弦项的傅里叶级数为余弦级数.
特殊情况：
1、如果函数 f(x)只在区间[-π,π]上有定义并满足收敛定理的条件,可将 f(x)周期延拓到整个实数轴上,即在(-∞,+∞)上作周期为2π的函数F(x),使F(x)在[-π,π)(或(-π,π])上等于f(x),即
将F(x)展开成傅里叶级数,则在(-π,π)上,由于 F(x)≡f(x),所以 F(x)的傅里叶级数收敛到 f(x),并且在区间端点处收敛到1/2[f(π-0)+ f(-π+ 0)].
奇延拓得到正弦级数，偶延拓得到余弦级数
2、如果函数f(x)定义在区间(0,π]上且满足收敛定理的条件,那么根据需要可把它展开为正弦级数或者余弦级数.首先在区间[-π,0]上补充函数f(x)的定义，得到定义在[-π,π]上为奇(偶)函数的F(x),这个过程称为奇(偶)延拓;然后将奇(偶)延拓后的函数F(x)按前面所讲方法展开成傅里叶级数，该级数必定是正弦(余弦)级数,限制在(0,π]上便是f(x)的正弦(余弦)级数.
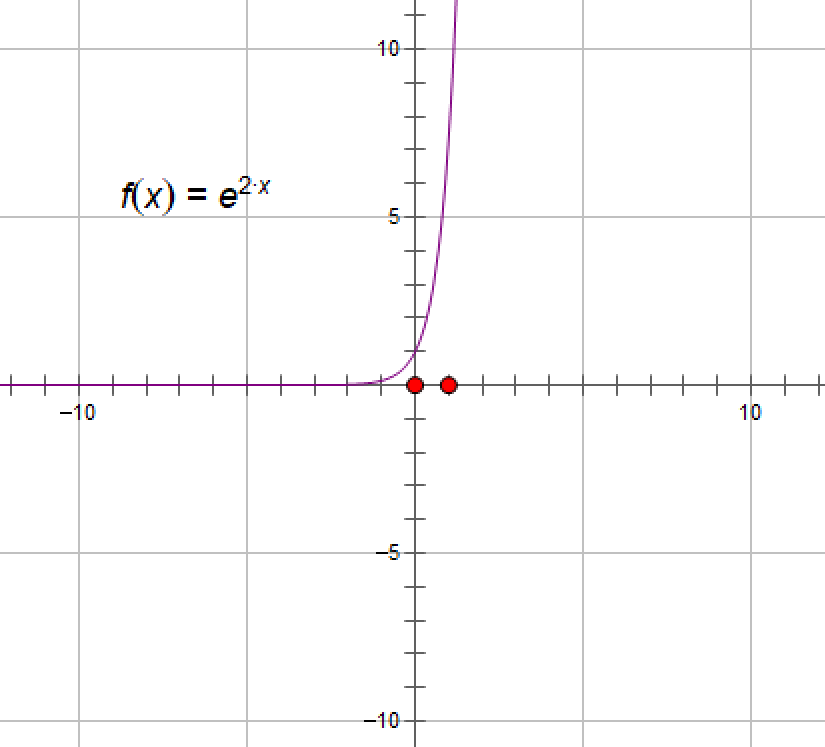
例11.6.3将函数f(x)=e2x在区间[0,π]上展开为余弦级数
函数图像如下：
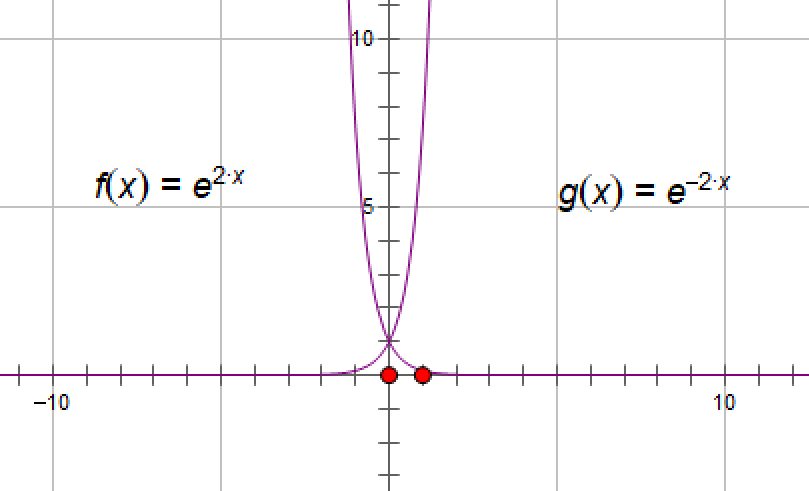
解 先对f(x)进行偶延拓,得到[-π,π」上的偶函数 F(x),故只含常数项和余弦项，于是
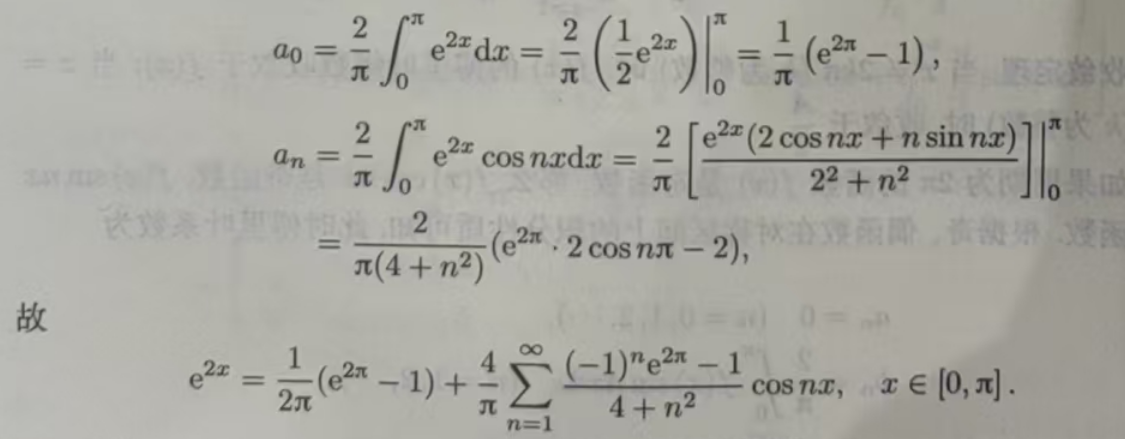
注如果将f(x)=e2x作奇延拓,就可以将其展开成正弦函数.
由于展开傅里叶级数只要考虑函数在区间[0，2π)(或(0,2π])上的函数值,因此非周期函数一样能展开成傅里叶级数.
3、周期为 2l的函数的傅里叶级数
对于周期为2l的函数，即f(x) = f(x+2l)，可以通过变量代换将其转变为周期为2π的函数
设周期为2l的函数f(x)满足收敛定理条件.作变量替代t=πx/l，x和t的值对应如下：
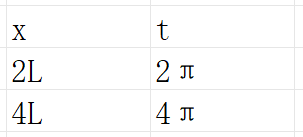
即f(x)的周期为2L，g(t)的周期为2π。
则g(t) = f(x) = f(tl/π)是周期为2π 的函数,且满足收敛定理条件,
由于g(t)是周期为2π的函数，其傅里叶级数为：
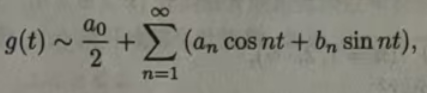
其中
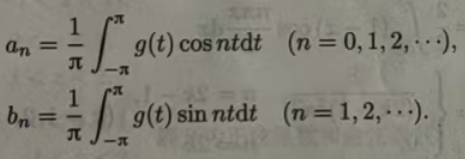
用t=πx/l将变量代回x ，cosnt = cosnπx/l，sinnt=sinnπx/l，
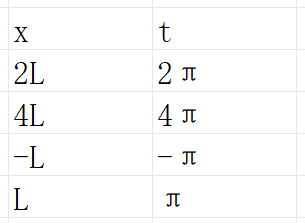即t从-π到π的积分，相当于x从-L到L进行积分
所以1/π∫ dt = 1/π∫ dπx/l = 1/L∫ dx
得到函数f(x)如下：
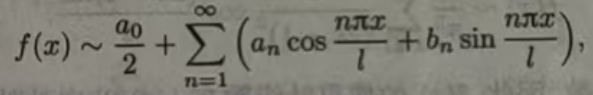(11.6.7)
其中
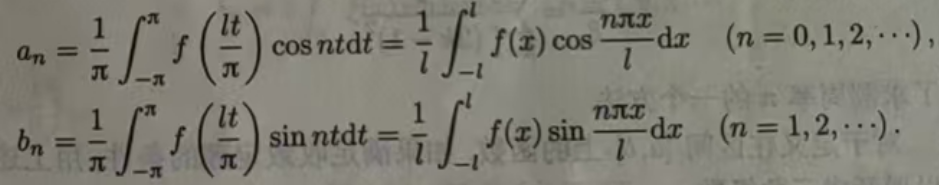
(11.6.7)式就是周期为2l的函数的傅里叶级数.
工程中周期为2l的函数的傅里叶级数的表达形式
在工程中x从0开始，周期T=2L，ω = π/L=2π/T，∫ dx从-L积到L，相当于∫ dx从0积到2L，也即从0积到T，新的表达方式如下：
问题：当T→∞时，f(x)不再是周期函数，那我们该如何处理呢？
类似于前面的讨论可得,当f(x)为奇函数时，那么f(x)cosnx 是奇函数,f(x)sinnx是偶函数.根据奇、偶函数在对称区间上的积分性质可知,此时傅里叶系数为
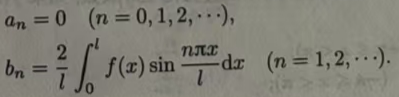
当f(x)为偶函数时,那么f(x)cosnx 是偶函数,f(x)sinnx是奇函数.根据奇、偶函数在对称区间上的积分性质（奇函数在对称区间积分的和为0）可知,此时傅里叶系数为
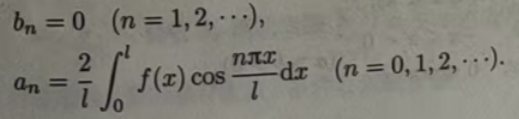
例11.6.4设f(x)是周期为4的周期函数,它在(-2,2]上的表达式为
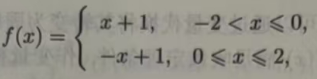
将 f(x)展开成傅里叶级数.
解 这时l=2,因为f(x)是偶函数,所以
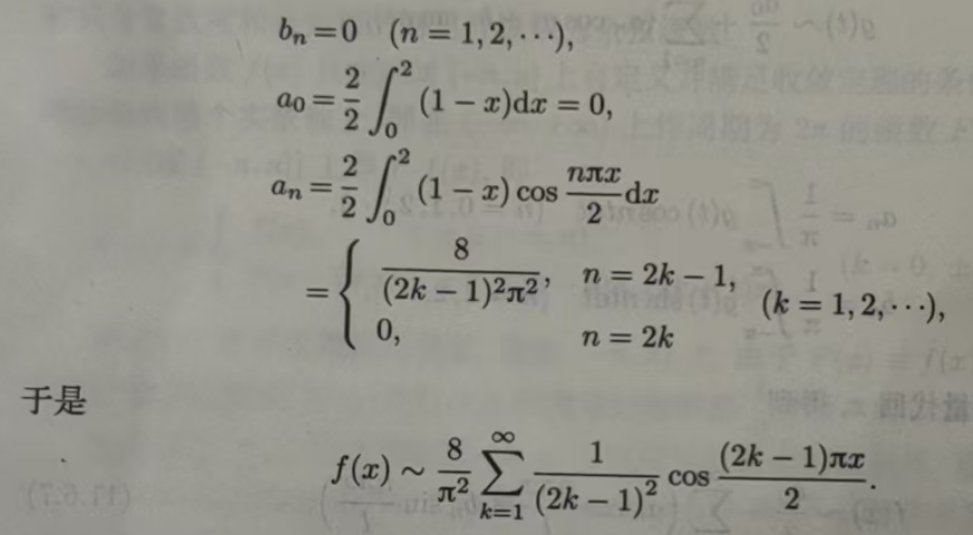
由于f(x)是连续函数,因此f(x)的傅里叶级数在(-2,2]内处处收敛于f(x).
如果令 x=0,得到
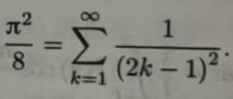
这给出了求圆周率π的一个方法.
注对于定义在区间[a,b]上的函数,如果满足收敛定理的条件,用上述方法同样可以展开成三角级数.
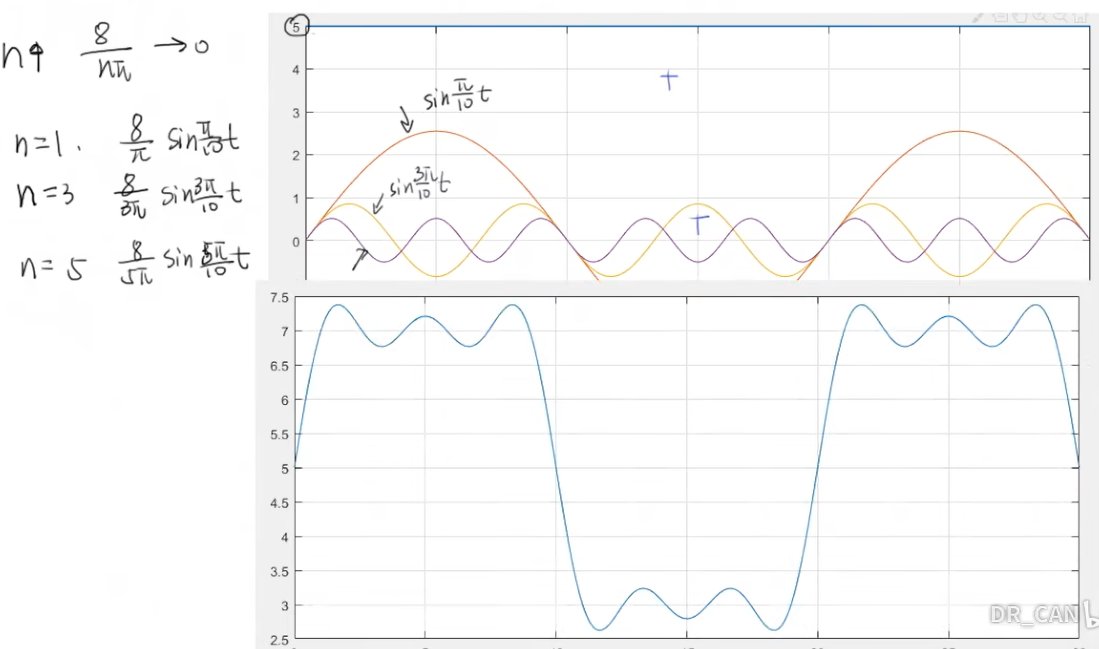
案例：将下面的周期函数f(t)展开成傅里叶级数
一个力施加在振动系统上，去分析一下系统的响应，先找到振动系统的固有频率，再分析周期函数的展开，再将两者进行对比，如果正好在固有频率上振幅过大的话，有可能会出问题。
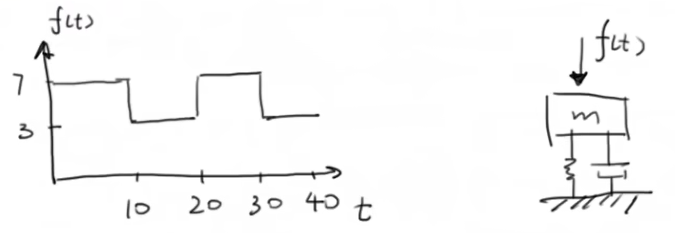
解：
通过答案，我们发现，随着n的增加，系数8/nπ会变得越来越小，趋近于0，对这个系统来说，低频率的正弦波占主要部分，而高频率要小的多。
4、欧拉公式
先来了解一下复数的概念：
形如a+bi（a、b均为实数）的数为复数，其中，a被称为实部，b被称为虚部，i为虚数单位。复数通常用z表示，即z=a+bi，当z的虚部b＝0时，则z为实数；当z的虚部b≠0时，实部a＝0时，常称z为纯虚数。i2 = -1
复数的模: 将复数的实部与虚部的平方和的正的平方根的值称为该复数的模，记作∣z∣。
即对于复数z=a+bi，它的模：
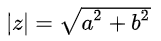
在复变函数中，自变量z可以写成z=r(cosθ+isinθ)，r是z的模，即r=|z|；θ是z的辐角，记作Arg(z)。
为了避免负数在实数范围内无法开偶数次方运算，我们将实数扩充到复数。实数范围内，平方根这样的偶数次方根对于负数是没有定义的，因为任何实数的平方都是非负的。比如，√(-1)在实数里是没有解的。这时候，数学家引入了虚数单位i，定义为i² = -1，这样负数就可以开平方了，例如√(-1) = i。进而将实数扩展为复数，复数的形式是a + bi，其中a和b都是实数，i是虚数单位。
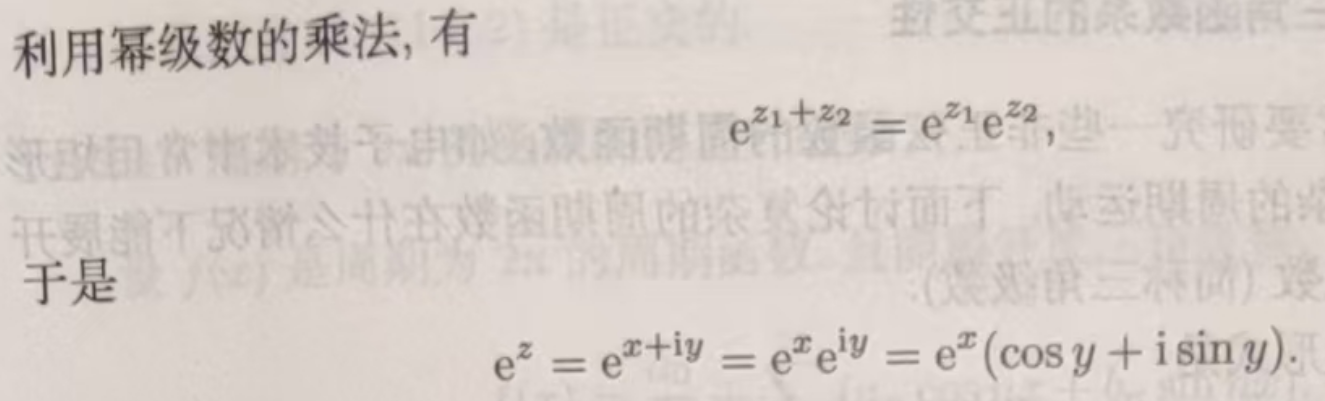
5、傅里叶级数的复数形式
由欧拉公式可知
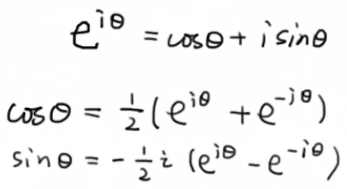
将上面的两个式子代入下面的傅里叶级数当中
结果如下所示：
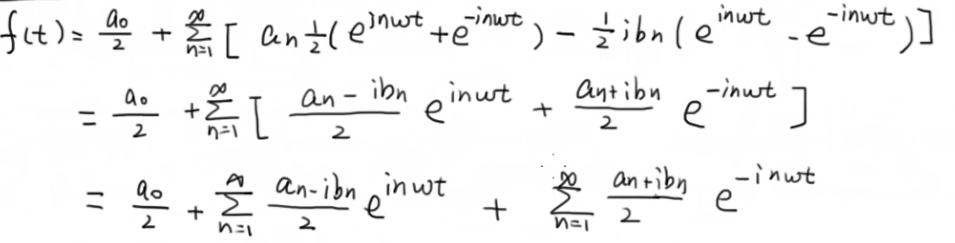
对于上面等式右边的第三项，将n变为-n，则右边第三项变为如下所示：
此时等式右边变为
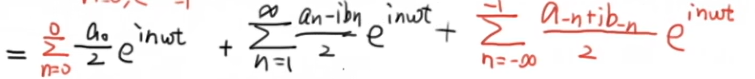
上面的第三项n从-∞到-1，第一项n从0到0，第二项n从1到∞，连在一起就变成了-∞到+∞，所以傅里叶级数的复数形式如下所示：
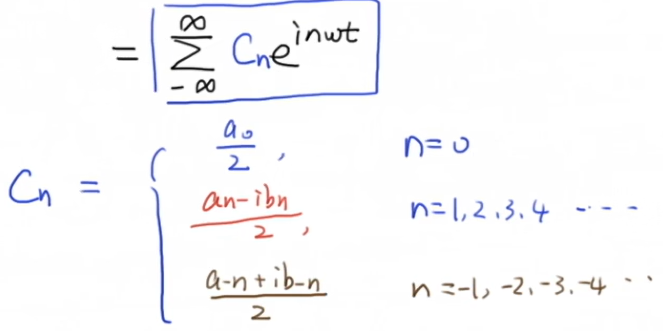
再根据a0、an、bn的值
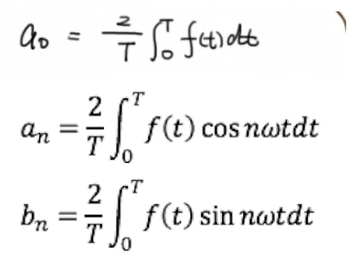
计算Cn的值
故傅里叶级数的复数形式如下：
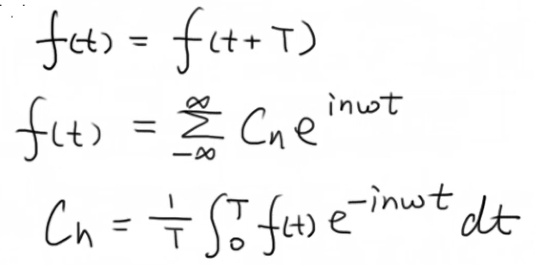
下面我们就可以令T趋向于无穷，去寻找非周期函数的变换，这就是傅里叶变换
三、傅里叶变换
上面讲过傅里叶级数的复数形式，如下所示：
1、周期函数
周期函数f(t)，用fT(t)表示
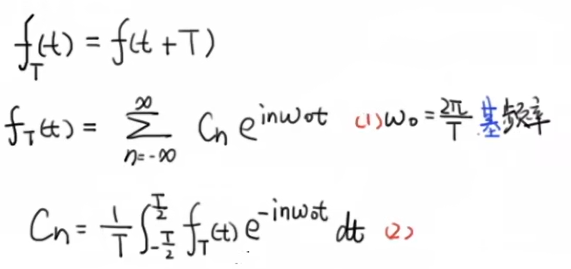
这里Cn从-T/2积到T/2，当然也可以从0积到T
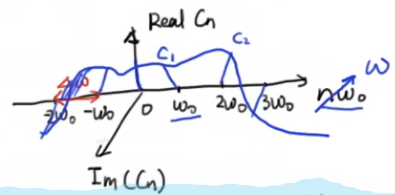
（1）式中Σ从-∞到∞和einw0t 对于任意的傅里叶级数来说都是一样的，而真正区分出不同函数的实际上是系数Cn，它定义了函数，这里Cn是复数，即Cn=a+ib的形式。我们把它在图像当中表达出来，令横轴为nω0，纵轴为Cn的实部部分Real，另外一条轴是Cn的虚部部分
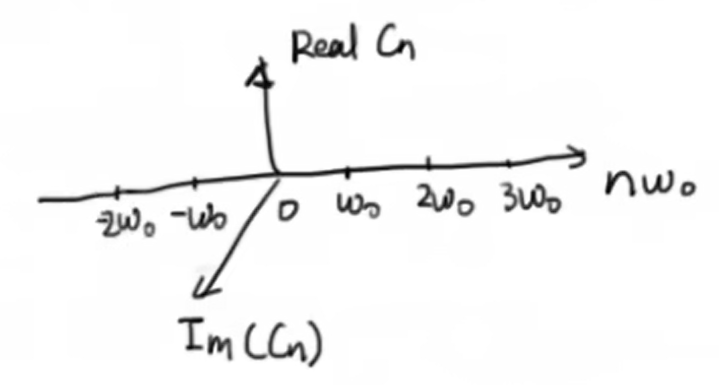
我们可以把相应的Cn在图上表达出来，我们用Cn乘以对应的复指数
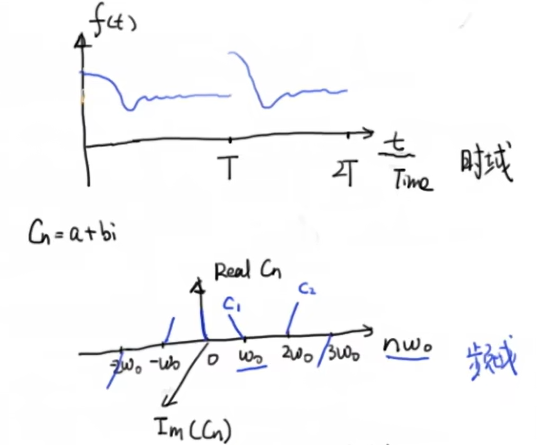
...+C-1ei-1ω0t + C0e0 +C1ei1ω0t +C2ei2ω0t + ...，所有的加起来，就可以得到和上面的图形一样的函数了，所以说下面的图是上面的函数在nω0为横坐标上的一个在复平面上的表达形式。在工程当中，上面的图是以时间为横坐标的，所以称为时域，下面的图 显示了在各种不同的频率下系数的值，我们称为频域，这幅图为上面时域图的频谱，这就是从不同的角度来看世界，每一种波形都会对应一种频谱，不过一般来说我们看到的频谱很少是这种复平面的三维的，有时候我们会把复数Cn的幅度单独拿出来，即|Cn|，这样我们就可以看到时间函数在不同频率下的强度。
2、非周期函数
对于非周期函数，我们能否找到更一般的表达形式呢？
非周期函数，就是不重复，换句话说就是无限久后重复，所以说它的周期趋近于无穷，当周期趋近于无穷时，带下标T的f(t)就变成了不带下标的f(t)，即一般形式
频谱中，两个频率之间的距离我们定义成Δω，Δω=(n+1)ω0 - nω0 = ω0 =2π/T，可以看出，随着T的不断增大，Δω就不断的减小，即距离就越来越小，从图中来看他们靠得越来越近，而当T无穷大的时候，他们的距离就没有了，即挨在一起，离散的形式变成了连续的形式，即三维空间中的一条曲线，这时就可以把横坐标由原来的nω0变为连续的变量ω
将下面的（2）式代入（1）式当中
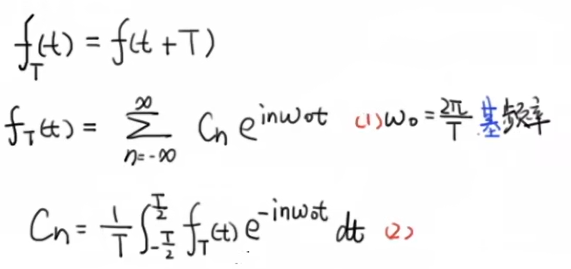
结果如下:
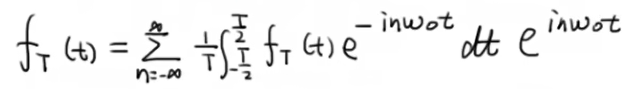
由于1/T=Δω/2π
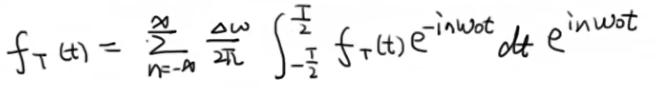
此时令T→∞，有：
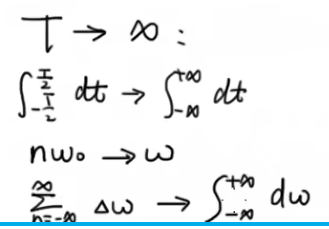
前面的Σ是n从-∞到∞，后面引入了Δω，就变成了ω从-∞到∞的积分了。代入f(t)中就有：
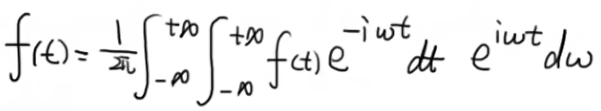
中间部分的积分就叫做傅里叶变换
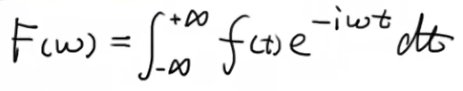
而原来的式子就叫逆傅里叶变换，如下所示:
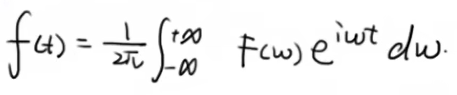
对于连续信号 f(t)，其傅里叶变换 F(ω) 定义为：
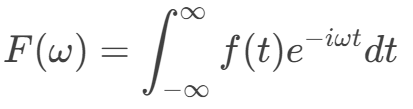
ω 是角频率，e−iωt 表示复指数形式的正弦波。
逆傅里叶变换则可以从频率域恢复原始信号：
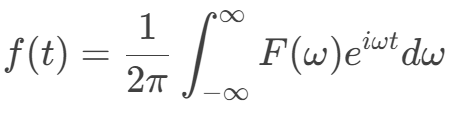
3、 二维离散傅里叶变换
为什么要在频率域研究图像增强？
可以利用频率成分和图像外表之间的对应关系。对于一个图像而言，大色块部分一般代表的是图像的低频成分，而它的一些轮廓是图像的高频成分。一些在空间域表述困难的增强任务，在频率域中变得非常普通。
滤波在频率域更为直观，它可以解释空间域滤波的某些性质。
可以在频率域指定滤波器，做反变换，然后在空间域使用结果滤波器作为空间域滤波器的指导。
一旦通过频率域试验选择了空间滤波，通常实施都在空间域进行。
二维离散傅里叶变换（2D-DFT）公式
图像尺寸为MXN的函数f(x,y)的DFT为:
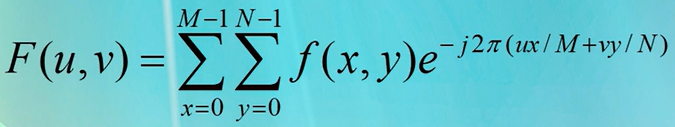
其中u=0,1,2,3,....,M-1,v=0,1,2,3,....,N-1
如果原始图片的尺寸为MxN的二维数组的话，那么得到的傅里叶变换也是MxN的数组。
给出F(u,v) ,可通过逆DFT得到f(x，y)
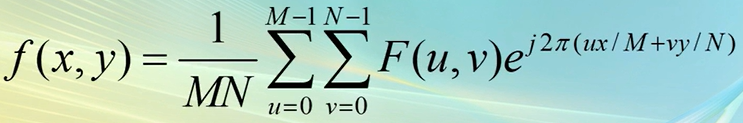
其中x=0,1,2,3,....,M-1,y=0,1,2,3,....,N-1
注意：u和v是频率变量，x和y是空间变量
二维DFT的性质----对称性
二维DFT的性质----周期性
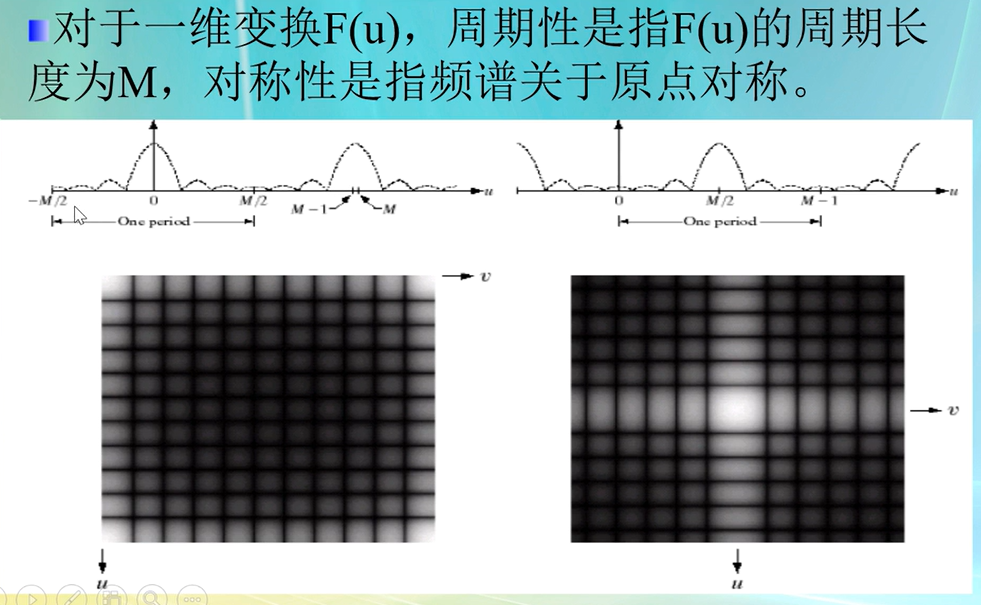
我们可以将周期性的频谱进行平移M/2
二维DFT的性质----卷积
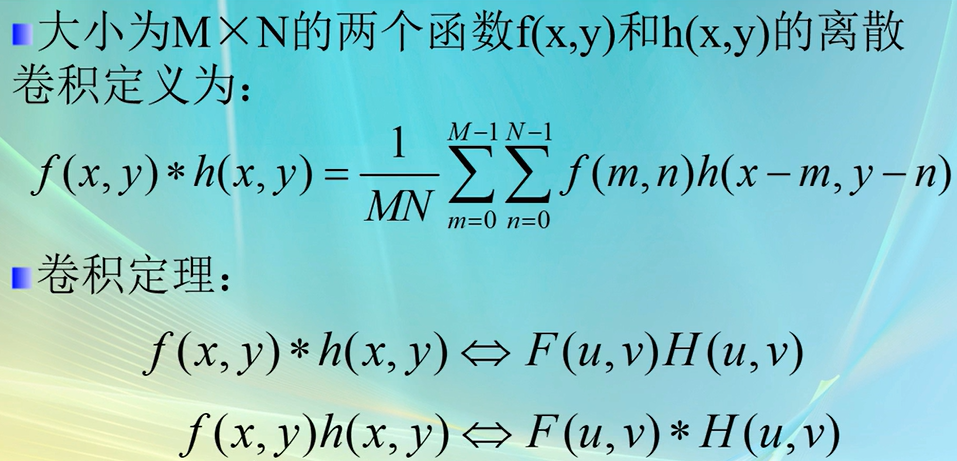
二维DFT的性质----相关
二维DFT的性质----自相关
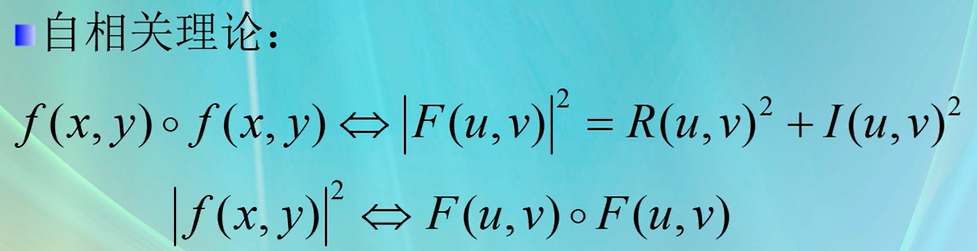
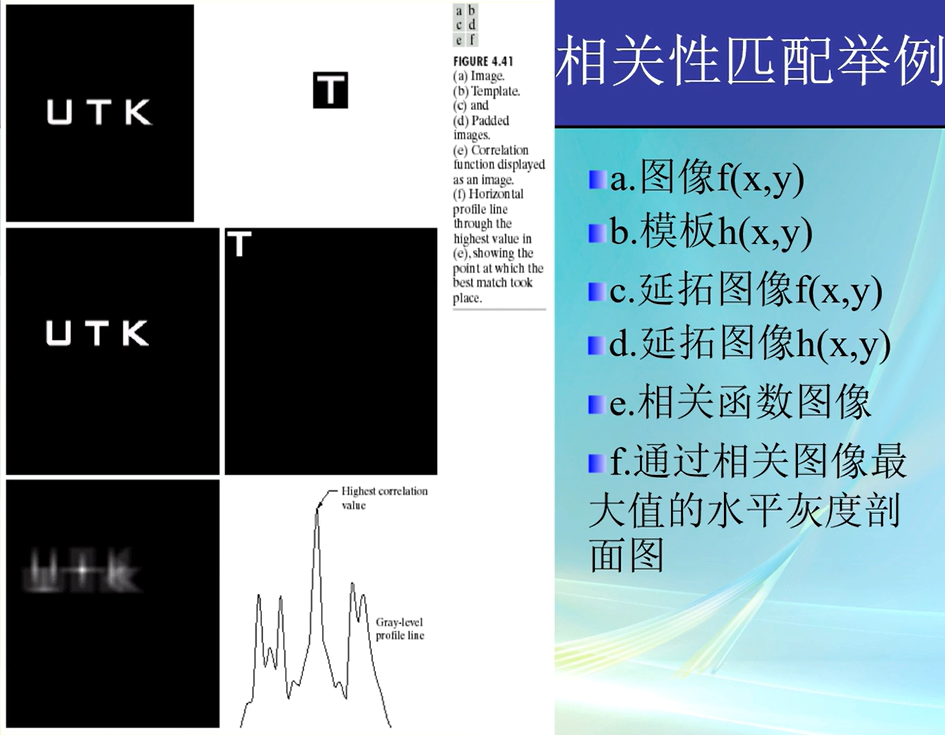
在MATLAB中计算和观察二维DFT
% 清除当前窗口 clc clear f = imread('./123.png'); imshow(f),title('原始图像') % 傅里叶变换 F = fft2(f); S = abs(F); figure,imshow(S, []), title('图像的频谱') Fc = fftshift(F); figure,imshow(abs(Fc), []),title('经过原点变换之后的频谱') S2 = log(1 + abs(Fc)); figure,imshow(S2, []),title('利用对数变换视觉增强后图像频谱')
结果：
4、理解
傅里叶变换只是一个时域函数与频域函数相互转化的工具而已
其强大之处在于：通过频域操纵时域，使时域中很难处理的信号变得轻而易举。
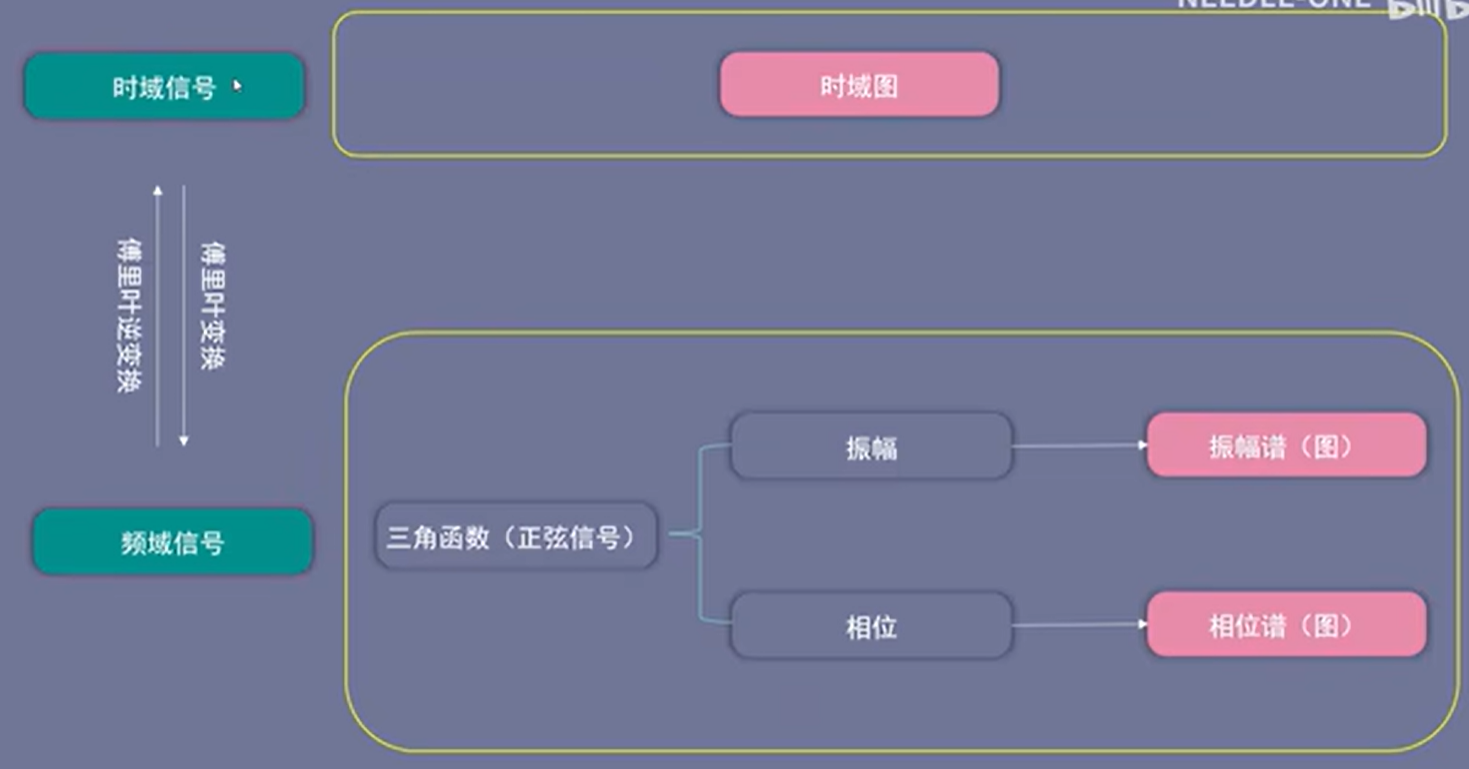
时域就是以时间为自变量，因变量随时间变化而变化，其图像成为时域图。
频域是由一堆简单的三角函数构成，通常是指正弦信号，这些三角函数的振幅构成了振幅谱，三角函数的相位构成相位谱，即频域只有振幅谱和相位谱两个图。总的来说就三个图：时域图、振幅谱、相位谱，
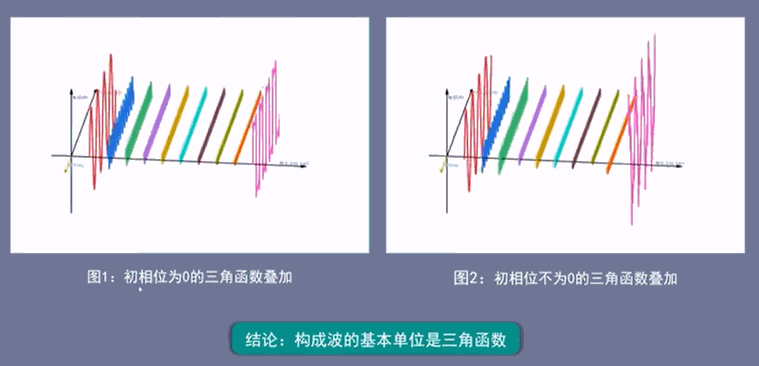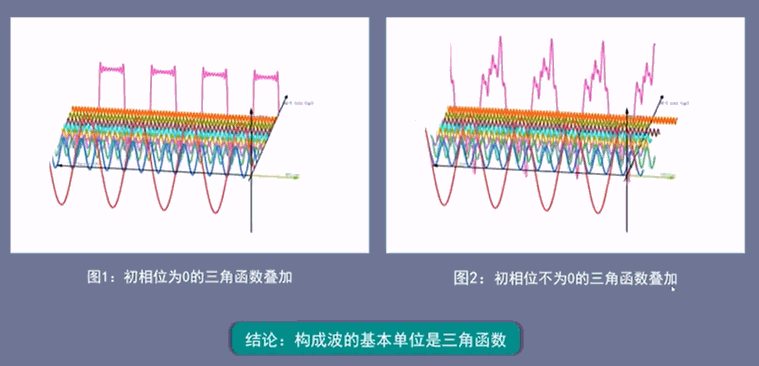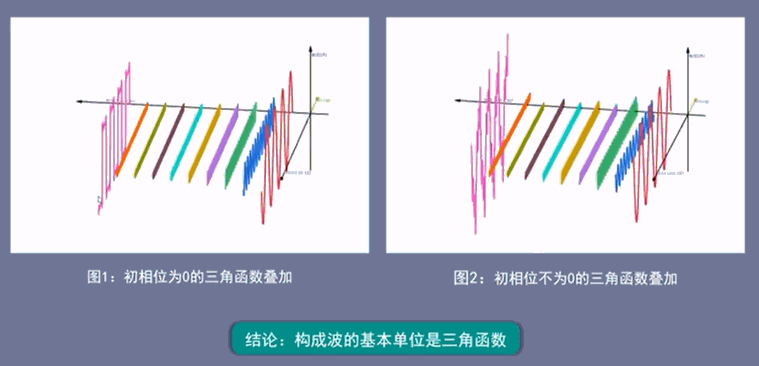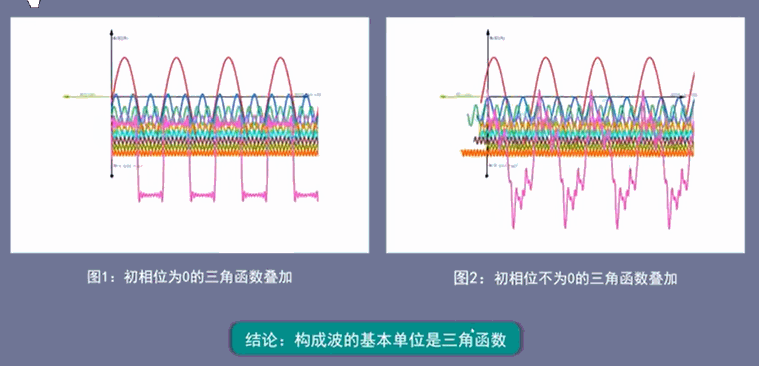
图1是一系列初相为0的三角函数，叠加后得到有规律的方波信号，
图2是一系列初相不为0的三角函数，叠加后得到无规律的杂乱信号，
从图上可以得到一个显而易见的结论：无论是图1有规律的方波信号，还是图2无规律的杂乱信号，其基本单位都是一些列有规律的三角函数，即构成波的基本单位为三角函数
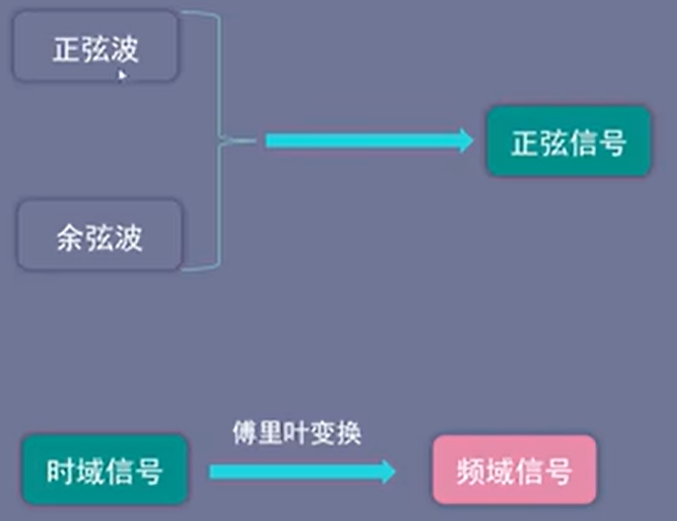
无论是正弦波还是余弦波，它们只是相差π/2的相位，可以统一看作是正弦信号
傅里叶变换的伟大之处是将复杂的时域信号变为频域的简单正弦波，
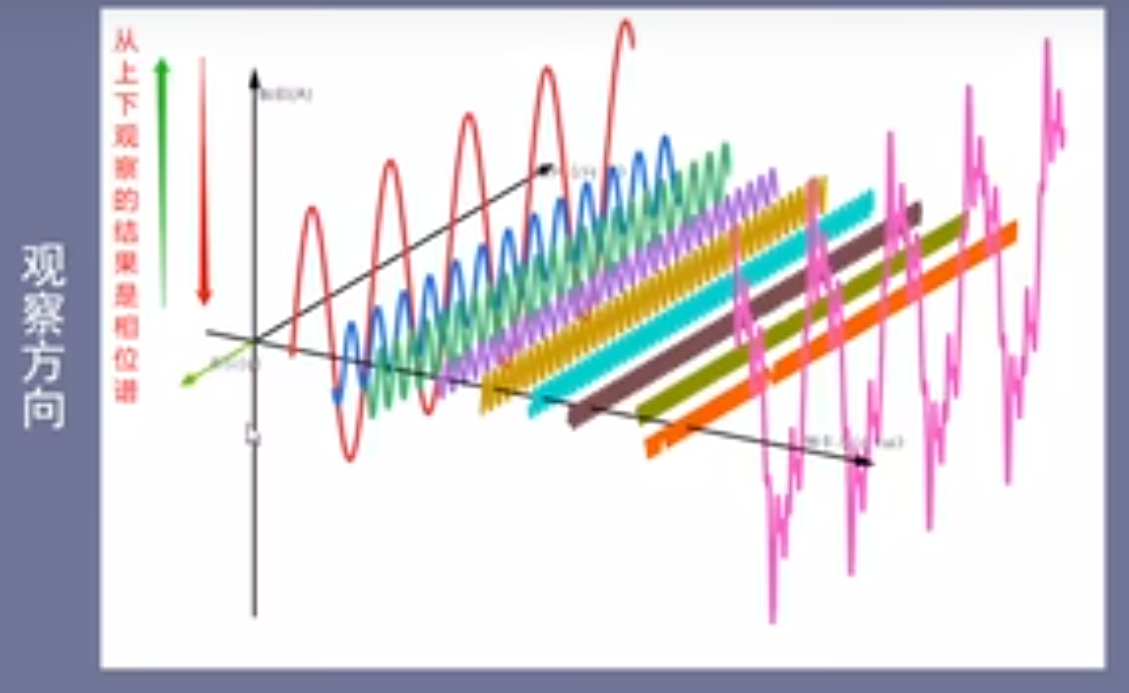
时域图：从左右方向观察的结果是时域图像
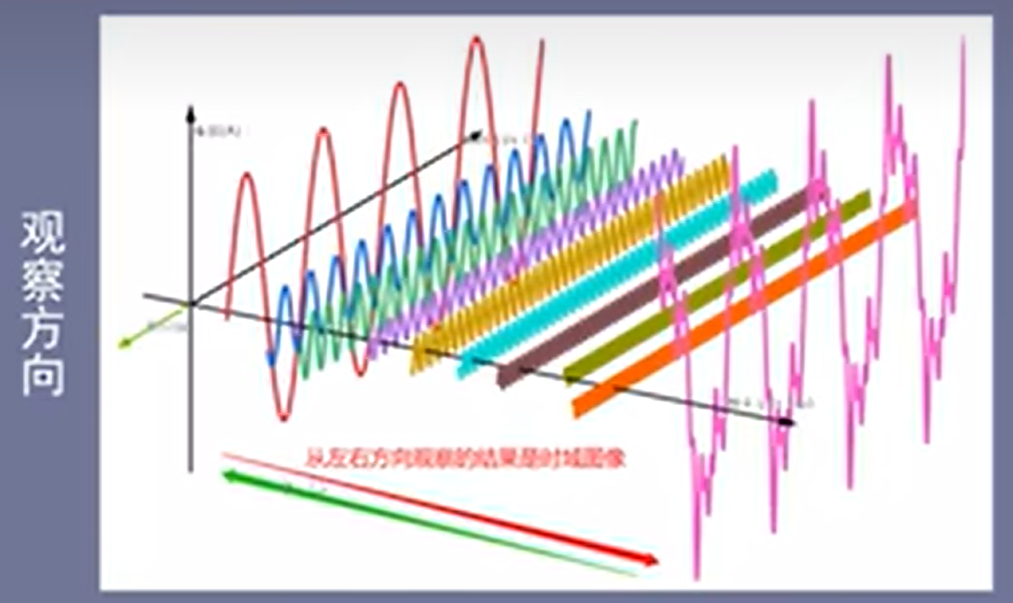
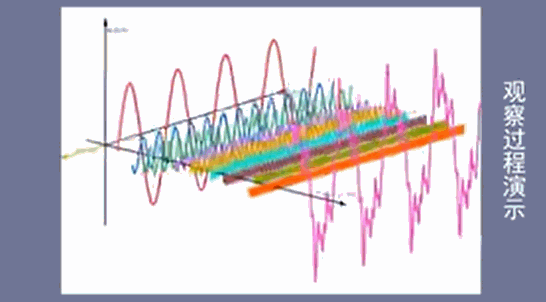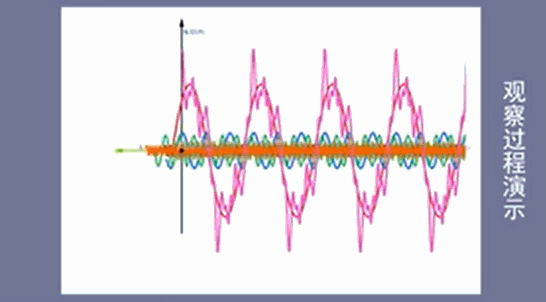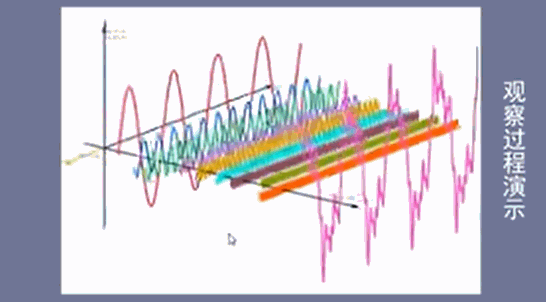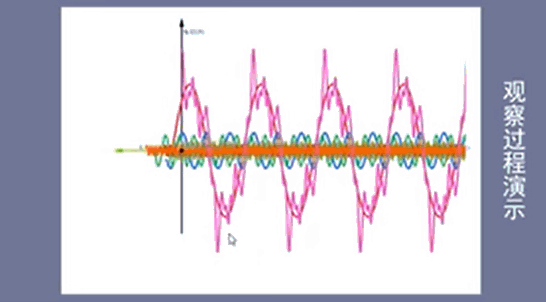
将叠加的正弦信号都去除后得到时域图
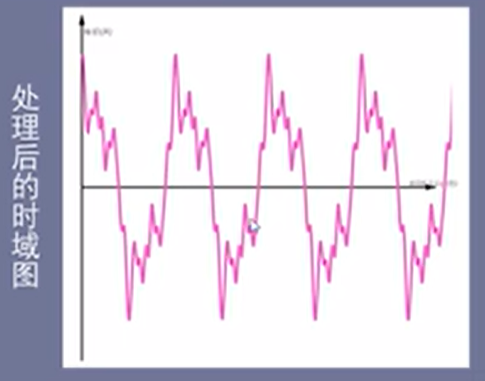
频域-振幅谱： 从前后观察的结果是振幅谱
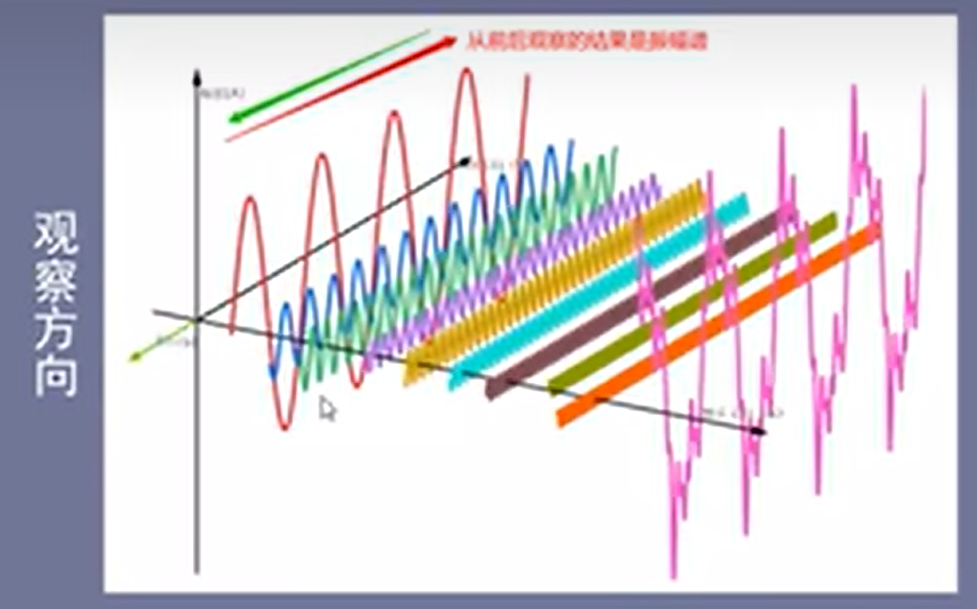
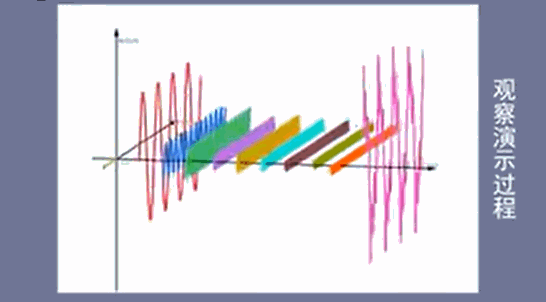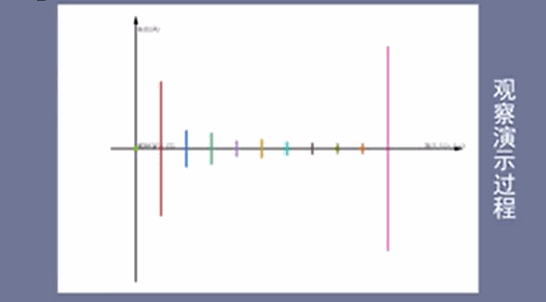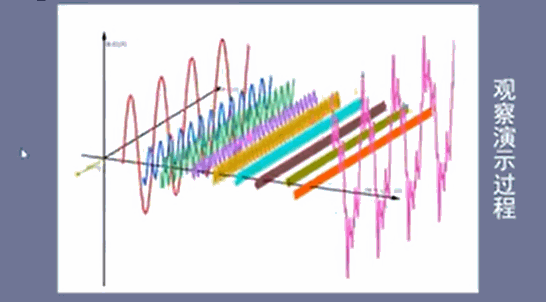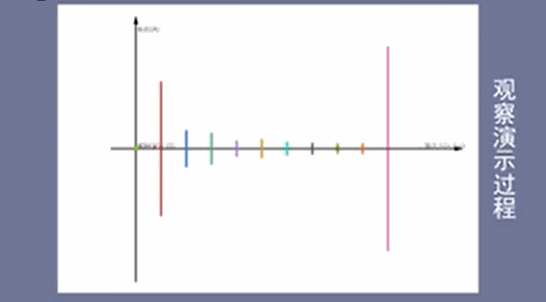
振幅谱：包含两个方向的振幅
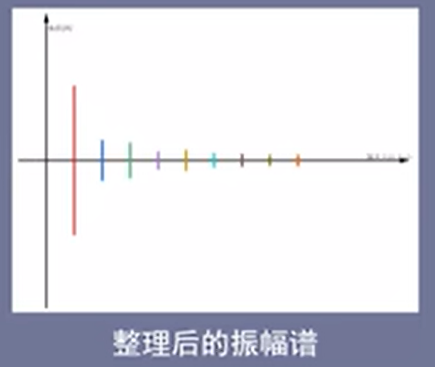
而正弦信号的振幅应该是一半，如下所示：
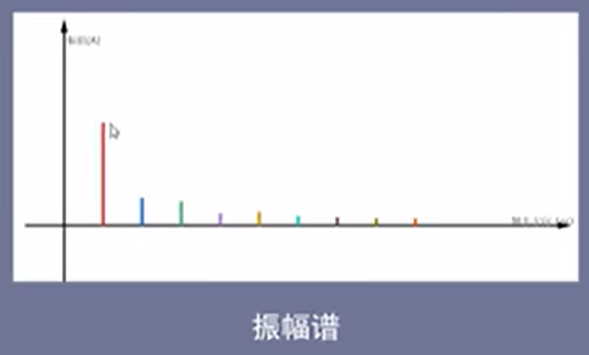
这是离散的傅里叶变换，但实际上的信号都不是离散的，而是连续的，那么该如何得到连续的频域图呢？首先将这些离散的正弦振幅用线连接起来，如果两个振幅之间的间隔非常小时，就可以认为无线趋近于连续的。
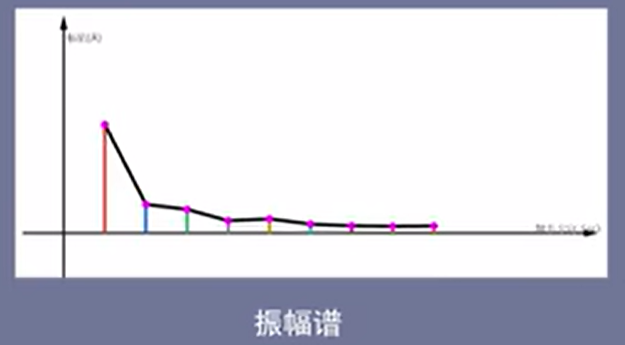
频域-相位谱：从上下观察的结果时相位谱。
以水平轴为界，去除相同的部分，剩下的就是相位谱了，如下图所示：
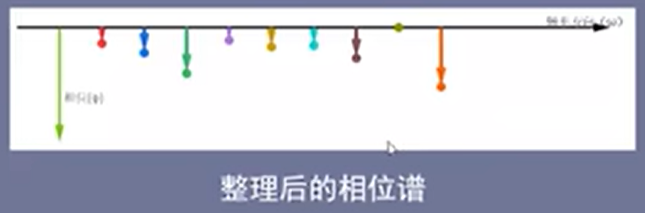
如果相位谱的相位很多，那么就可以认为是连续的相位谱了。
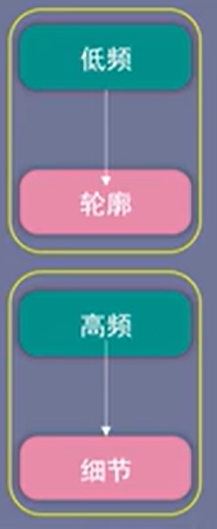
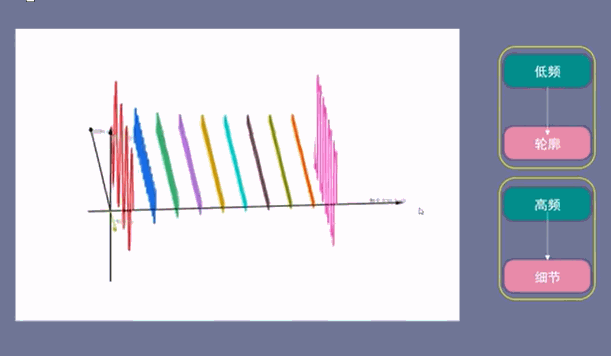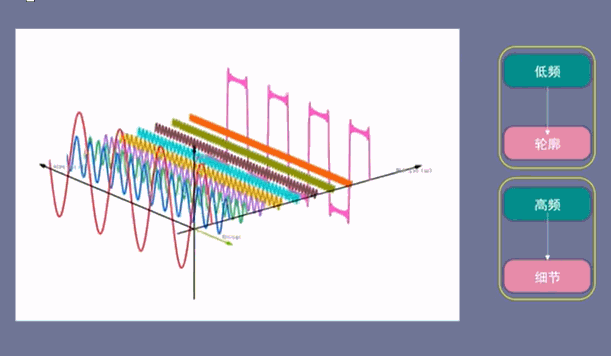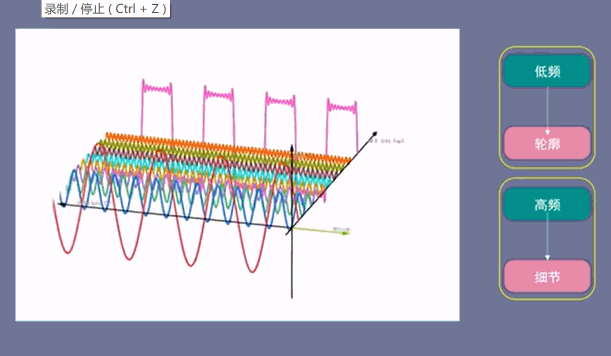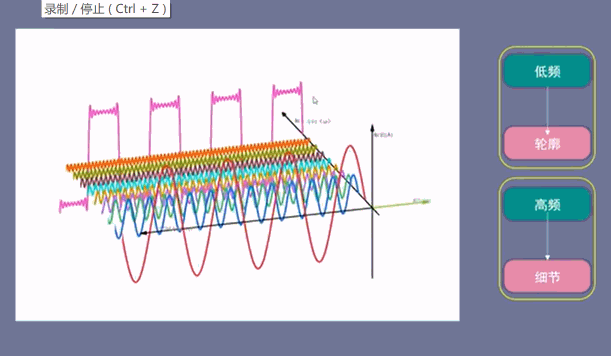
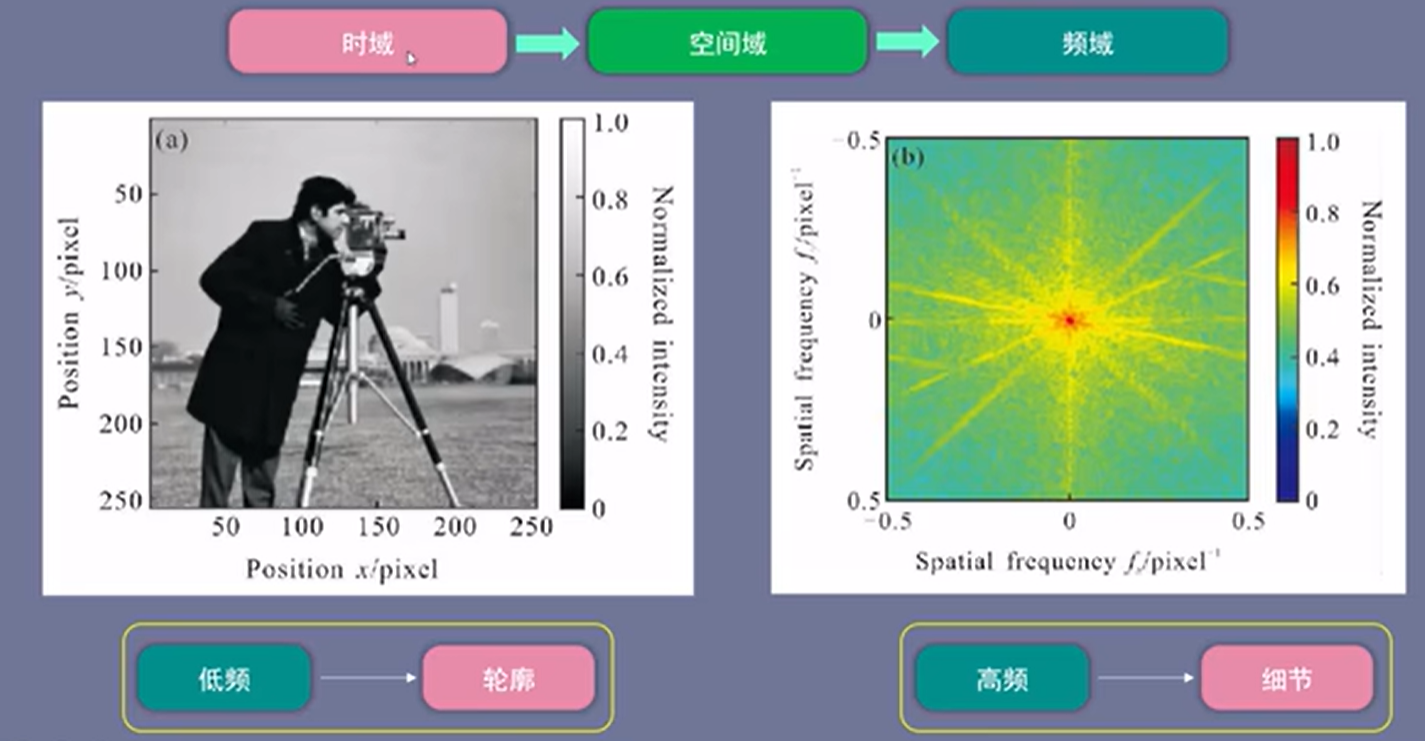
低频信号描绘了轮廓，而高频信号描绘了细节。
下面的图中，第一个低频信号（红色）决定了时域信号的大小，而后面的高频信号决定了时域信号的细节情况，弄懂了这个原理，在应用中就可以得心应手了。
傅里叶变换的应用：
就图像处理举例：先将时域改成空间域，再将空间域转变为频域，左图是空间域图像，第二张图是通过傅里叶变换得到的频域图像。
只通过频域图像是很难想象空间域是什么图像的，如果想处理图片的轮廓，我们可以对频域的低频信号进行处理，如果想处理图片的细节，那么就对频域的高频信号进行调整，这就是磨皮的原理。
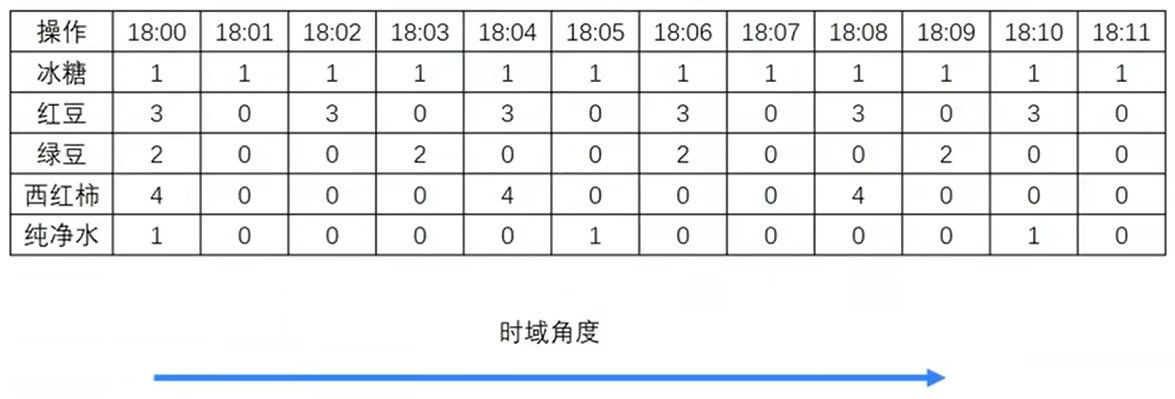
某饮料制作过程
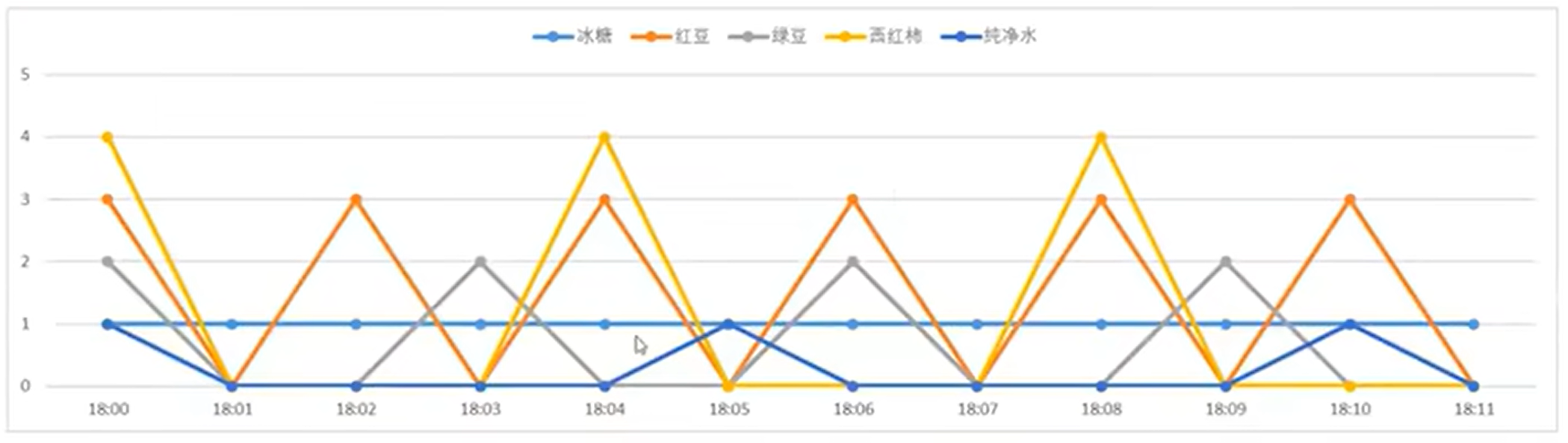
用图来表示:
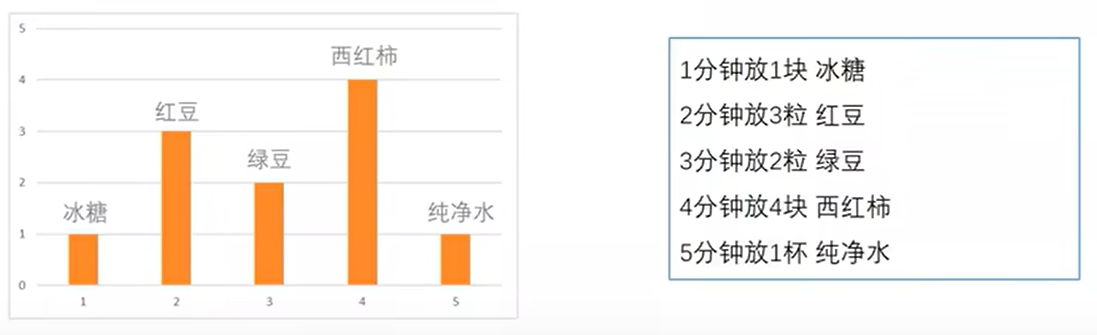
换一种角度表述：
即每隔1分钟放1块冰糖，每隔2分钟放3粒红豆，每隔3分钟放2粒绿豆，每隔4分钟放4块西红柿，每隔5分钟放1杯纯净水。
用图表示：
频率和周期是倒数的关系。T=2π/ω，
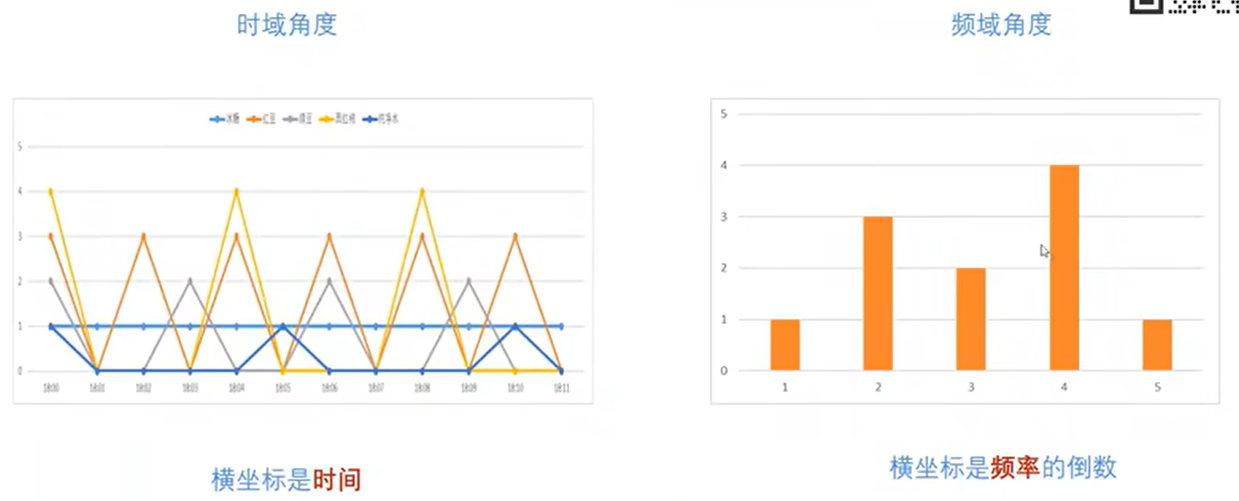
左边是时间空间，是动态的，右边是频率空间，是静止的，即从频率的角度看这个世界是静止的。
考虑更精准的时间问题：
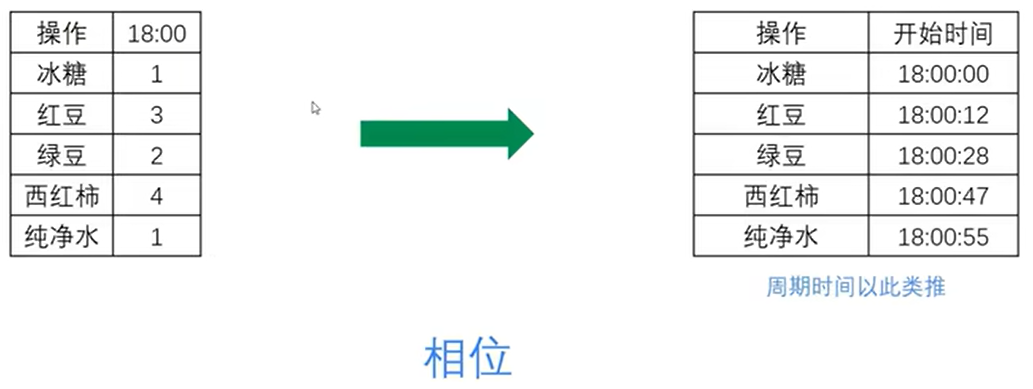
有一个时间差，在傅里叶变换中叫相位，相位是与时间差有关的一个表述。
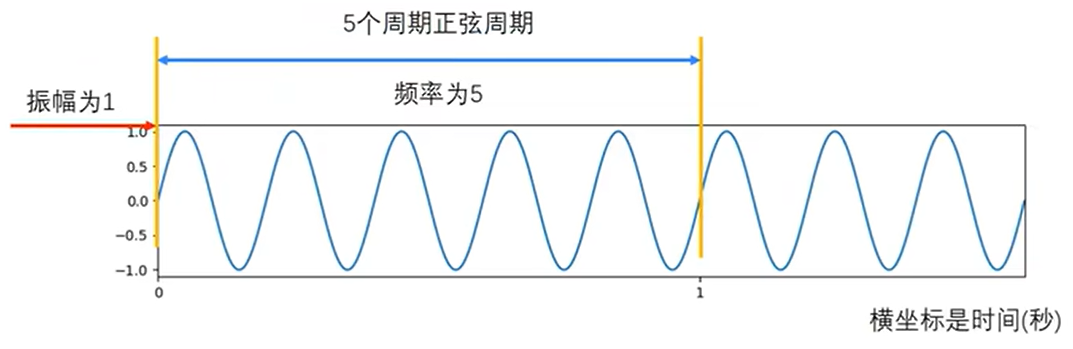
下面看正弦函数sinx,1秒钟经过5个周期，即频率是5，振幅是1，
时域角度
频域角度
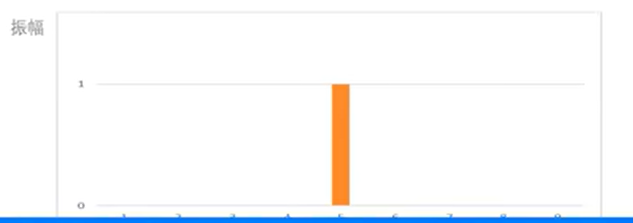
横坐标是频率，在频率为5的位置有一个柱子，柱子的振幅为1.
实际上上面两个图是等价的，上面表示的是一个正弦的曲线，以时间为单位，1秒钟过5个周期。下面是从静止的角度去看的，在频率为5的位置有一个柱子，柱子的振幅为1，与上面的描述是一样的。
或者说这两者是可逆的，上边的可以推导得到下面的，反之也一样。
任何一个正弦曲线都可以从频率的角度表示，任何连续周期信号，可以由一组适当的正弦曲线组合而成。所以说傅里叶认为所有的周期信号都可以表示为一个频域，
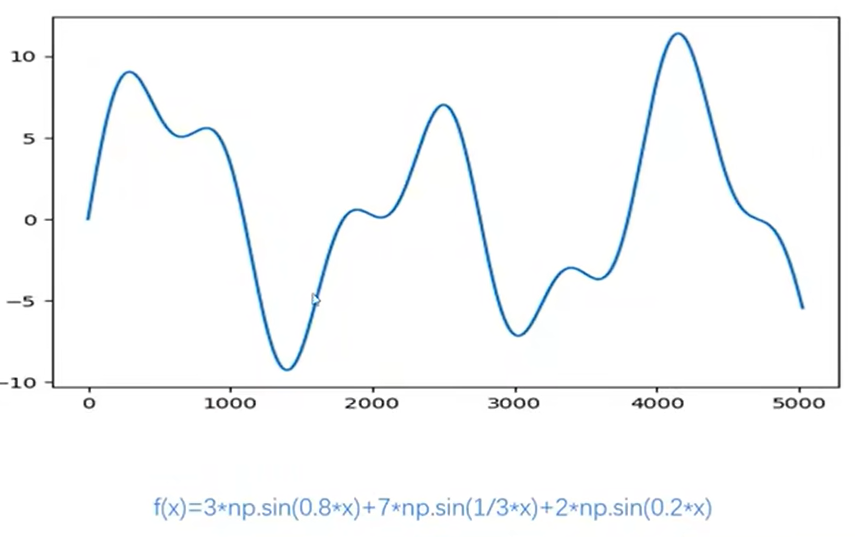
这条曲线非常复杂，但是经过傅里叶变换可以表述成一系列的正弦函数
f(x) = 3*sin(0.8*x) + 7*sin(1/3*x) + 2*sin(0.2*x),该函数的图像由下面的三个正弦曲线组合而成
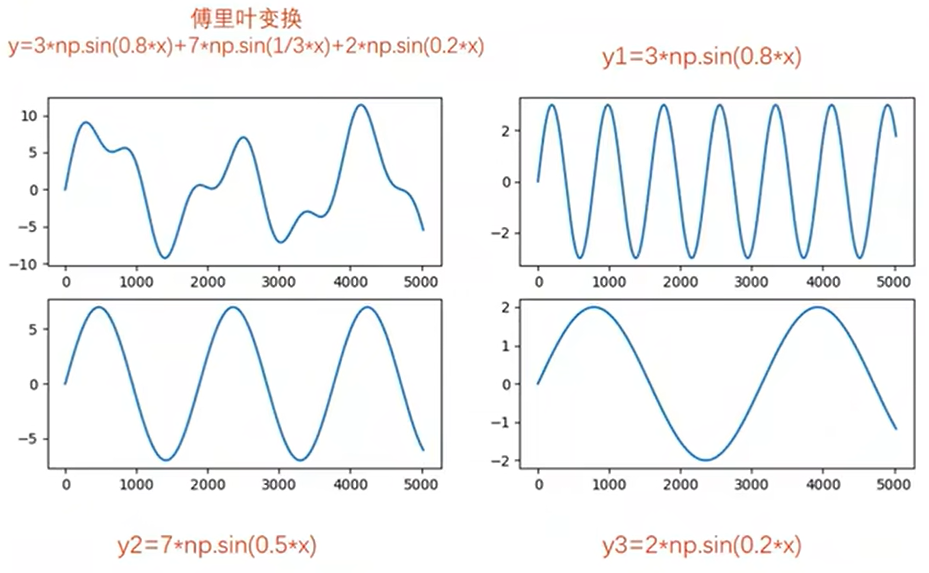
3个正弦曲线的初相都为0，即都是从0开始的。组合得到的曲线也是从零开始的。
上面三个正弦曲线可以用频率来表示，如下图所示：
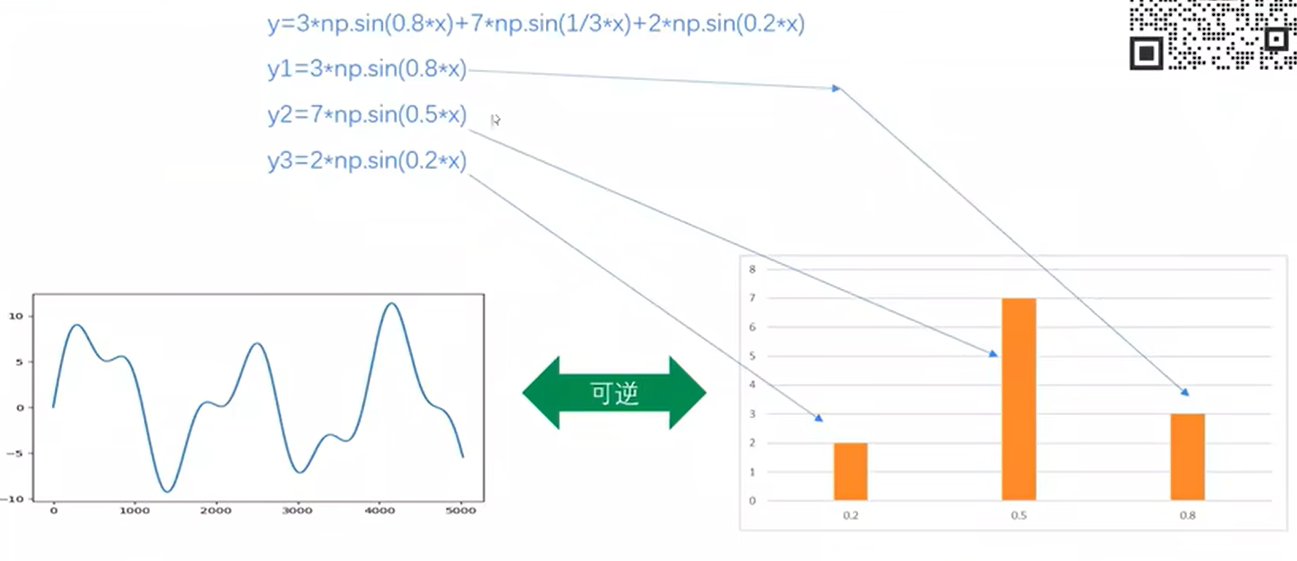
横坐标为频率，纵坐标为振幅。
傅里叶变换是可逆的，能够由时域推导出右边的频域，能够由右边的频域反推得到左边的时域。
相位：不是同时开始的一组余弦函数，在叠加时要体现开始的时间。
相位与时间差有关系，
开始的起点不一致组成的曲线，函数为f(x) = 3*sin(0.8*x) + 7*sin(1/3*x + 2) + 2*sin(0.2*x + 3),
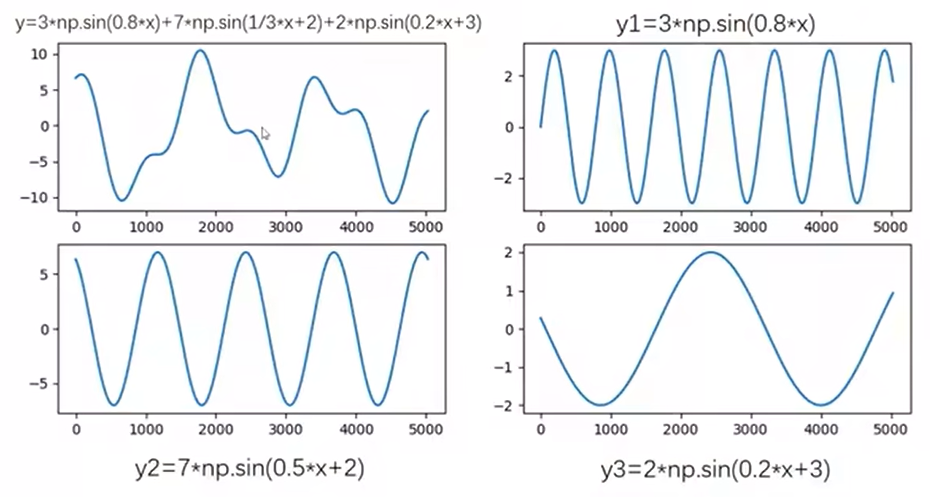
上图中时间不是同时开始的了，y1从0开始，y2从2开始，y3从3开始，他们三个的开始时间不一致，得到了与上面不同的曲线。
总结：傅里叶变换是从时域来看函数（或信号）转换成从频率的角度去看函数（或信号），而且他们是可逆的。
实际应用场景
-
信号处理：
-
降噪（识别并滤除特定频率的噪声）。
-
压缩音频/图像（保留主要频率成分，丢弃次要成分）。
-
-
通信技术：
-
WiFi、5G 信号调制与解调。
-
雷达信号分析。
-
-
物理学：
-
量子力学中的波函数分析。
-
光学中的衍射现象研究。
-
傅里叶变换的“家族”
-
傅里叶级数：针对周期性信号，分解为离散频率的正弦波（例如：方波分解）。
-
离散傅里叶变换（DFT）：计算机处理实际信号时使用的数值方法。
-
快速傅里叶变换（FFT）：DFT 的高效算法，广泛应用于实时信号处理（如手机通话）。
四、Numpy实现快速傅里叶变换
numpy中封装了快速Fourier算法，即FFT，根据数值范围、正反变换以及数组维度，共有下表这些函数可供使用，其前缀i表示逆变换。
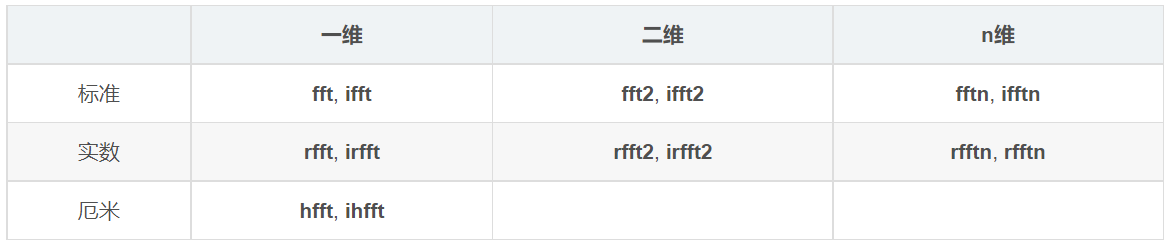
此外，还有获取频率和相位的两组函数fftfreq, rfftfreq, fftshift, ifftshift。
numpy实现傅里叶变换函数：
1、numpy.fft.fft2实现傅里叶变换，返回一个复数数组(complex ndarray)，fft2中的2表示处理的是二维信号。
2、numpy.fft.fftshift将零频率分量移到频谱中心
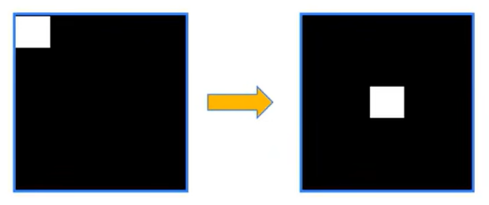
通过傅里叶变换得到频谱图像，频谱图像的低频（白色是低频）在它的左上角，为了观看起来更直观（实际上是为了将来好替换），我们一般会将它放置到中心点，即将低频移动到频谱图像的中心位置。
3、20*np.log(np.abs(fshift)) 设置频谱的范围
即先对得到的频谱图像计算绝对值，再计算log值，最后乘以20
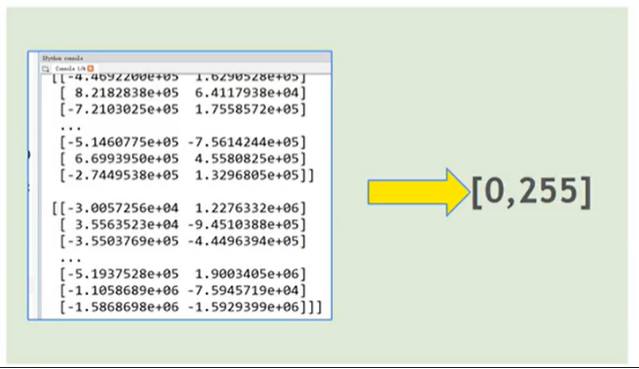
傅里叶变换numpy.fft.fft2得到的是复数的数组，我们需要给复数数组重新标定范围，或者说设置它的区间，即映射到[0,255]区间之内。因为复数数组是没法通过图像的形式展示出来的，我们要把它转成灰度图像，
代码介绍
import torch import numpy as np import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt from numpy.fft import * import cv2 img = cv2.imread('./lena.png',0) # 0表示保持灰度模式 print(img.shape) print("img: ",img) # gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 转换为灰度图像 f = np.fft.fft2(img) # 进行傅里叶变换，得到频谱（复数的数组），频谱图像的低频位于左上角 print("f: ",f) fshift = np.fft.fftshift(f) # 将零频率分量移到频谱中心，得到的fshift仍然是复数数组 print("fshift: ",fshift) result = 20*np.log(np.abs(fshift)) # 设置频谱的范围为[0,255] plt.subplot(121) plt.imshow(img,cmap='gray') plt.title('gray') plt.axis('off') plt.subplot(122) plt.imshow(result, cmap='gray') plt.title('result') plt.axis('off') plt.show()
结果：
(512, 512) img: [[162 161 161 ..., 170 154 129] [161 161 161 ..., 173 155 125] [161 161 162 ..., 170 155 128] ..., [ 43 42 51 ..., 103 101 98] [ 40 41 55 ..., 102 104 106] [ 41 43 57 ..., 101 106 109]] f: [[ 3.24271370e+07 +0.j -4.56410673e+05+2391037.49470229j 1.53683665e+06-1137891.92005507j ..., -2.39081135e+05 -636469.1844251j 1.53683665e+06+1137891.92005506j -4.56410673e+05-2391037.4947023j ] [ -2.81106978e+04-1227017.71286657j -1.59206203e+06+1591726.68441919j -1.10910120e+06 +83585.55938053j ..., 6.51690693e+05 +811089.51822276j -3.56018601e+05 +449288.11345675j 3.64327508e+04 +944233.95218021j] [ -4.48996764e+05 -165472.38651542j -2.75547531e+05 -132112.38880421j 6.66269825e+05 -454933.68144214j ..., 3.52374900e+05 +925823.4692072j -7.22966027e+05 -175108.31860443j 8.21480108e+05 -62086.87105315j] ..., [ 5.17583262e+05 -212719.00940893j 7.35457788e+05 +708444.46047738j -5.25386789e+05 -200957.88629785j ..., 9.94004453e+05 +115384.35995933j 1.34408539e+05 -679404.33877189j -5.81014283e+04 +605403.30150711j] [ -4.48996764e+05 +165472.38651542j 8.21480108e+05 +62086.87105314j -7.22966027e+05 +175108.31860444j ..., -5.13519218e+05 -756506.91014434j 6.66269825e+05 +454933.68144214j -2.75547531e+05 +132112.38880421j] [ -2.81106978e+04+1227017.71286657j 3.64327508e+04 -944233.95218021j -3.56018601e+05 -449288.11345675j ..., -5.19520237e+05+1901794.23496531j -1.10910120e+06 -83585.55938052j -1.59206203e+06-1591726.68441917j]] fshift: [[ -641.00000000 +0.j -48.90077031 -81.0544397j 559.17917041 +349.47951499j ..., 160.29717880+1845.1430523j 559.17917041 -349.47951499j -48.90077031 +81.0544397j ] [ -466.97325662 +317.95372052j -276.56862171+1217.21725989j -6.76761347 -562.4574378j ..., -298.66840014-1051.05323442j -48.70699453 -612.12613021j 93.26690370 +386.46049709j] [ 1092.71342513 -297.54827373j 28.83441067 +206.89809691j -929.76380032 +815.62894778j ..., 120.95403701 -838.02883685j -796.51877675 -78.91618223j 565.74121311 +345.2953466j ] ..., [ -334.96377606 +268.06165323j 420.99987350 +748.61650857j 308.27881526 -680.6489225j ..., -174.00620371 +386.32585869j 248.22202879 +139.89736577j 91.25847698-1629.51389599j] [ 1092.71342513 +297.54827373j 565.74121311 -345.2953466j -796.51877675 +78.91618223j ..., 36.80785521 +137.90895789j -929.76380032 -815.62894778j 28.83441067 -206.89809691j] [ -466.97325662 -317.95372052j 93.26690370 -386.46049709j -48.70699453 +612.12613021j ..., -1148.28134984 +716.43295824j -6.76761347 +562.4574378j -276.56862171-1217.21725989j]]
注意
（1）、傅里叶得到低频、高频信息，针对低频、高频处理能够实现不同的目的。
（2）、傅里叶过程是可逆的，图像经过傅里叶变换、逆傅里叶变换后，能够恢复到原始图像
（3）、在频域对图像进行处理，在频域的处理会反映在逆变换图像上
五、Numpy实现逆傅里叶变换
逆傅里叶变换：由通过傅里叶变换得到的频谱图像转为原始图像
为什么进行了傅里叶变换之后还要进行逆傅里叶变换？
这是为了在频域对图像进行处理。我们进行傅里叶变换就是为了得到图像的低频和高频，然后对低频或高频进行处理，最后恢复原始图像，只不过在频域的处理会反映在逆变换图像上。
对低频进行处理指的是只保留低频或舍弃低频。低频就是图像的细节，如果只保留低频，实现的是低通滤波，图像会比较模糊，边界被我们去掉了。如果只保留高频，叫高通滤波，边界会被保留，但是细节会丢失，图像的对比度也会发生变化。
numpy实现逆傅里叶变换函数：
（1）、numpy.fft.ifft2 实现逆傅里叶变换，返回一个复数数组(complex ndarray)
（2）、numpy.fft.ifftshiftfftshift函数的逆函数，将低频从频谱图像的中心移动到左上角
（3）、iimg=np.abs(逆傅里叶变换结果) 设置值的范围
逆傅里叶变换得到的也是一个复数的数组，复数的数组无法显示成图像，或者说不在灰度图像范围内，所以将复数映射到[0,255]之间，直接取绝对值就可以实现。
代码介绍
import torch import numpy as np import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt from numpy.fft import * import cv2 img = cv2.imread('./lena.png',0) # 0表示保持灰度模式 f = np.fft.fft2(img) # 进行傅里叶变换，得到复数的数组，频谱图像的低频位于左上角 fshift = np.fft.fftshift(f) # 将零频率分量移到频谱中心，得到的fshift仍然是复数数组 ishift = np.fft.ifftshift(fshift) # 将低频分量移到左上角 iimg = np.fft.ifft2(ishift) # 逆傅里叶变换，返回复数数组，而复数无法显示为图像 iimg = np.abs(iimg) # 映射为[0,255] plt.subplot(121) plt.imshow(img,cmap='gray') plt.title('original') plt.axis('off') plt.subplot(122) plt.imshow(iimg, cmap='gray') plt.title('iimg') plt.axis('off') plt.show()
结果：
目标图像和原始图像应该是一模一样的。
六、高通滤波演示
1、在频域（傅里叶域）进行高通滤波
低频
低频对应图像内变化缓慢的灰度分量。例如，在一幅大草原的图像中，低频对应着广袤的颜色趋于一致的草原。
低频指图像中大量存在的细节信息。
高频
高频对应图像内变化越来越快的灰度分量，是由灰度的尖锐过渡造成的。例如，在一幅大草原的图像中，其中狮子的边缘等信息。
高频指轮廓
衰减高频而通过低频，低通滤波器，将模糊一幅图像（去掉轮廓）。
衰减低频而通过高频，高通滤波器将增强尖锐的细节（只保留轮廓），但是会导致图像的对比度降低。
滤波
接受(通过)或者拒绝一定频率的分量。
低通滤波器
通过低频的滤波器称为低通滤波器
高通滤波器
通过高频的滤波器称为高通滤波器
频域滤波
将图像由空域变成频域，在频域内修改傅里叶变换（的低频或高频）以达到特殊目的，然后计算IDFT返回到图像域:
特殊目的:图像增强、图像去噪、边缘检测、特征提取、压缩、加密等
离散傅里叶反变换（inverse discrete Fourier transform）简称IDFT，一种数字变换的逆变换。discrete /dɪˈskriːt/ 离散
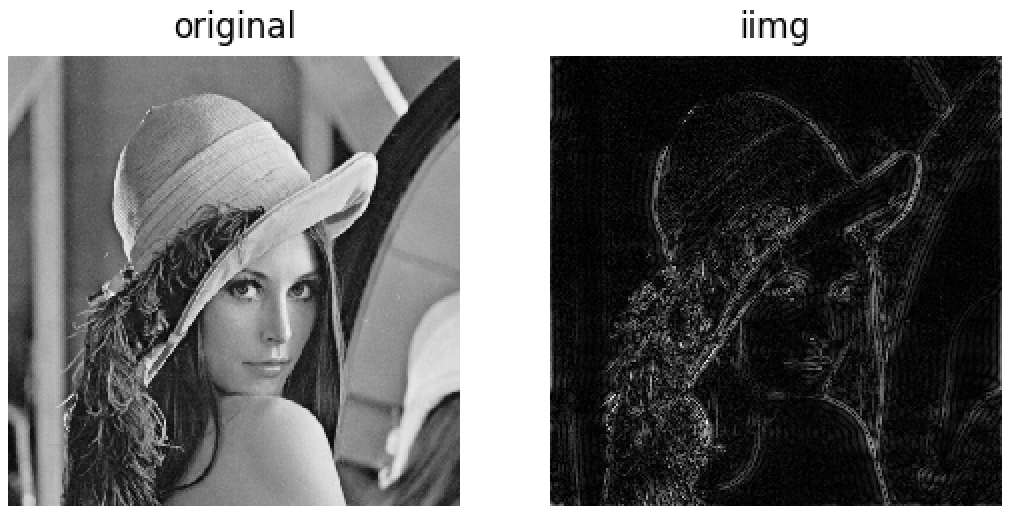
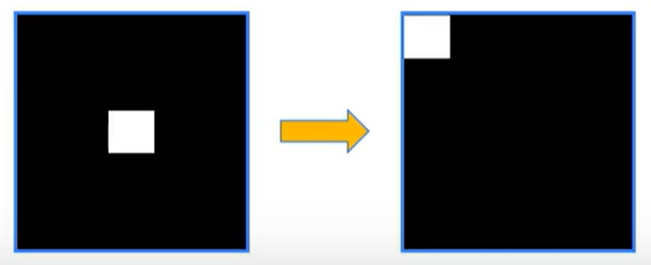
将低频（中间亮的部分，即白色部分，255）覆盖掉，
即原先的255变成0，即得到的都是高频，效果如下：
高通滤波器去掉低频，代码如下：
rows, cols = img.shape # 获取图像的高宽 crow,ccol = int(rows/2),int(cols/2) # 获取中心点坐标 fshift[crow-30:crow+30,ccol-30:ccol+30]=0
效果如下：
代码演示：
import torch import numpy as np import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt from numpy.fft import * import cv2 img = cv2.imread('./lena.png',0) # 0表示保持灰度模式 f = np.fft.fft2(img) # 进行傅里叶变换，得到复数的数组，频谱图像的低频位于左上角 fshift = np.fft.fftshift(f) # 将零频率分量移到频谱中心，得到的fshift仍然是复数数组 rows, cols = img.shape # 获取图像的高宽 crow,ccol = int(rows/2),int(cols/2) # 获取中心点坐标 fshift[crow-30:crow+30,ccol-30:ccol+30]=0 ishift = np.fft.ifftshift(fshift) # 将低频分量移到左上角 iimg = np.fft.ifft2(ishift) # 逆傅里叶变换，返回复数数组，而复数无法显示为图像 iimg = np.abs(iimg) # 映射为[0,255] plt.subplot(121) plt.imshow(img,cmap='gray') plt.title('original') plt.axis('off') plt.subplot(122) plt.imshow(iimg, cmap='gray') plt.title('iimg') plt.axis('off') plt.show()
结果：
七、OpenCV实现离散傅里叶变换
OpenCV 实现傅里叶变换函数
（1）、返回结果=cv2.dft(原始图像，转换标识)
返回结果 是双通道的。第1个通道是结果的实数部分。第2个通道是结果的虚数部分。
原始图像:输入图像要首先转换成np.float32 格式，一般的图像都是8位二进制，np.float32(img)强制转换成符合要求的格式
转换标识:flags=cv2.DFT_COMPLEX_OUTPUT，输出一个复数阵列。
（2）、numpy.fft.fftshift将零频率分量移到频谱中心
通过傅里叶变换得到频谱图像，频谱图像的低频（白色是低频）在它的左上角，为了观看起来更直观（实际上是为了将来好替换），我们一般会将它放置到中心点，即将低频移动到频谱图像的中心位置。
（3）、返回值=cv2.magnitude(参数1，参数2) 计算幅值。
因为傅里叶变换的结果是一个复数，我们需要把复数映射到[0,255]区间从而可以显示成图像。
参数1:浮点型X坐标值，也就是实部
参数2:浮点型Y坐标值，也就是虚部
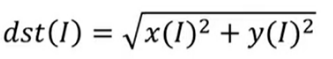
代码介绍：
import torch import numpy as np import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt from numpy.fft import * import cv2 img = cv2.imread('./lena.png',0) # 0表示保持灰度模式 # 使用dft函数进行傅里叶变换，参数1为原始图像，要转换为float32， dft = cv2.dft(np.float32(img),flags=cv2.DFT_COMPLEX_OUTPUT) # f = np.fft.fft2(img) # 进行傅里叶变换，得到频谱（复数的数组），频谱图像的低频位于左上角 dffshift = np.fft.fftshift(dft) # 将零频率分量移到频谱中心，得到的dffshift仍然是复数数组
print(dffshift)
print(dffshift.shape) # (512,512,2) # 将复数数组映射到[0,255] result = 20*np.log(cv2.magnitude(dffshift[:, :, 0],dffshift[:, :, 1])) # 设置频谱的范围为[0,255] plt.subplot(121) plt.imshow(img,cmap='gray') plt.title('original') plt.axis('off') plt.subplot(122) plt.imshow(result, cmap='gray') plt.title('result') plt.axis('off') plt.show()
dffshift[:, :, 0] 前面连个冒号分别表示行和列，第三个参数0表示第0个通道，如果是1表示第1个通道。两个通道分别显示
结果：
控制台打印dffshift的值：
[[[ 0. -641. ] [ -81.05371094 -48.90063477] [ 349.48016357 559.17919922] ..., [ 1845.14306641 160.29882812] [ -349.48016357 559.17919922] [ 81.05371094 -48.90063477]] [[ 317.95361328 -466.97314453] [ 1217.21118164 -276.56665039] [ -562.45349121 -6.77026367] ..., [-1051.05541992 -298.67529297] [ -612.12597656 -48.70800781] [ 386.45117188 93.26879883]] [[ -297.54833984 1092.71325684] [ 206.89294434 28.837677 ] [ 815.62866211 -929.76220703] ..., [ -838.02758789 120.95068359] [ -78.91604614 -796.515625 ] [ 345.29501343 565.73217773]] ..., [[ 268.0612793 -334.96374512] [ 748.61791992 421.0012207 ] [ -680.65087891 308.27758789] ..., [ 386.32421875 -174.00717163] [ 139.89782715 248.22186279] [-1629.52294922 91.25195312]] [[ 297.54821777 1092.71325684] [ -345.29501343 565.73217773] [ 78.91604614 -796.515625 ] ..., [ 137.902771 36.80810547] [ -815.62866211 -929.76220703] [ -206.89294434 28.837677 ]] [[ -317.95385742 -466.97314453] [ -386.45117188 93.26879883] [ 612.12597656 -48.70800781] ..., [ 716.43261719 -1148.27978516] [ 562.45349121 -6.77026367] [-1217.21118164 -276.56665039]]]
双通道表示第2维只有两个数，三通道表示第二维有3个数。
八、OpenCV实现逆傅里叶变换
openCV 逆傅里叶变换函数
（1）、返回结果=cv2.idft(原始数据)
idft是dft函数的逆函数
返回结果:取决于原始数据的类型和大小。
原始数据:实数或者复数均可。
（2）、返回值=cv2.magnitude(参数1，参数2) 计算幅值。
参数1:浮点型X坐标值，也就是实部
参数2:浮点型Y坐标值，也就是虚部
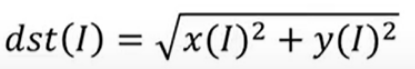
（3）、numpy.fft.ifftshift 将低频从频谱图像的中心移动到左上角
fftshift函数的逆函数。
代码介绍：
import torch import numpy as np import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt from numpy.fft import * import cv2 img = cv2.imread('./lena.png',0) # 0表示保持灰度模式 dft = cv2.dft(np.float32(img),flags=cv2.DFT_COMPLEX_OUTPUT) # 进行傅里叶变换 dftshift = np.fft.fftshift(dft) # 将零频率分量移到频谱中心，得到的fshift仍然是复数数组 ishift = np.fft.ifftshift(dftshift) # 将低频分量从频谱图像中心移到左上角 iImg = cv2.idft(ishift) # 逆傅里叶变换，得到的是复数数组，双通道 iImg = cv2.magnitude(iImg[:, :, 0], iImg[:, :, 1]) # 映射到[0,255] plt.subplot(121) plt.imshow(img,cmap='gray') plt.title('original') plt.axis('off') plt.subplot(122) plt.imshow(iImg, cmap='gray') plt.title('iimg') plt.axis('off') plt.show()
结果：
九、低通滤波示例
在频域进行低通滤波
（1）、对原始图像进行傅里叶变换得到右边的频谱图像，低频被移动到中间的位置
（2）、把频谱中间的部分保留，其他部分都变成黑色
得到的效果如下：
低频都通过了，高频即轮廓信息被舍弃掉了，所以图像看起来就模糊了很多。
将低通滤波器与频谱图像进行乘法运算，得到滤波的结果图像
那么如何构造低通滤波器呢？
构造一个二维数组，数组的值都是0，把中间部分的值设置为1。
rows, cols = img.shape crow,ccol = int(rows/2), int(cols/2) mask = np.zeros((rows,cols,2),np.uint8) # 构造一个二维数组，值全为0 mask[crow-30:crow+30,ccol-30:ccol+30]= 1 # 将中间的值设置为1
代码介绍
import torch import numpy as np import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt from numpy.fft import * import cv2 img = cv2.imread('./lena.png',0) # 0表示保持灰度模式 dft = cv2.dft(np.float32(img),flags=cv2.DFT_COMPLEX_OUTPUT) # 进行傅里叶变换 dftshift = np.fft.fftshift(dft) # 将零频率分量移到频谱中心，得到的fshift仍然是复数数组 rows, cols = img.shape crow, ccol = int(rows/2), int(cols/2) mask = np.zeros((rows, cols, 2), np.uint8) # 构造一个二维数组，值全为0 mask[crow-30:crow+30, ccol-30:ccol+30] = 1 # 将中间的值设置为1 fShift = dftshift*mask ishift = np.fft.ifftshift(fShift) # 将低频分量从频谱图像中心移到左上角 iImg = cv2.idft(ishift) # 逆傅里叶变换，得到的是复数数组，双通道 iImg = cv2.magnitude(iImg[:, :, 0], iImg[:, :, 1]) # 映射到[0,255] plt.subplot(121) plt.imshow(img,cmap='gray') plt.title('original') plt.axis('off') plt.subplot(122) plt.imshow(iImg, cmap='gray') plt.title('iimg') plt.axis('off') plt.show()
结果：
浙公网安备 33010602011771号