五校联考模拟赛Day2T2矩阵(容斥原理)
题意
$n * m$的网格,对其进行黑白染色,问每一行每一列至少有一个黑格子的方案数。
Sol
考场上只会$n^3$的dp,还和指数级枚举一个分qwq
设$f[i][j]$表示到了第$i$行,已经有$j$列被染黑,然后暴力转移上一行有几个黑格子
正解是容斥
首先固定好列,也就是保证每一列都有一个黑格子
这样的方案是$(2^N - 1) ^M$
然后容斥行
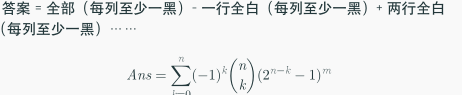
组合数暴力算即可
#include<cstdio> #include<cstring> #include<algorithm> #include<map> #include<vector> #include<set> #include<queue> #include<cmath> #include<iostream> #define Pair pair<int, int> #define MP(x, y) make_pair(x, y) #define fi first #define se second #define int long long #define LL long long //#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1<<22, stdin), p1 == p2) ? EOF : *p1++) //char buf[(1 << 22)], *p1 = buf, *p2 = buf; using namespace std; const int MAXN = 1e6 + 10, INF = 1e9 + 10, mod = 1e9 + 7; const double eps = 1e-9; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int N, M; LL fac[MAXN], ifac[MAXN], po2[MAXN]; LL fastpow(int a, int p) { LL base = 1; while(p) { if(p & 1) base = (base * a) % mod; a = (a * a) % mod; p >>= 1; } return base % mod; } LL C(int N, int M) { return fac[N] * ifac[M] % mod * ifac[N - M] % mod; } main() { N = 2 * 1e5; fac[0] = 1; po2[0] = 1; for(int i = 1; i <= N; i++) fac[i] = i * fac[i - 1] % mod, po2[i] = (po2[i - 1] * 2) % mod; ifac[N] = fastpow(fac[N], mod - 2); for(int i = N; i >= 1; i--) ifac[i - 1] = (ifac[i] % mod * i) % mod; N = read(); M = read(); int d = 1; LL ans = 0; for(int i = 0; i <= N; i++, d *= -1) ans = (ans + d * C(N, i) * fastpow((po2[N - i] - 1 + mod) % mod, M) % mod + mod) % mod; cout << ans; return 0; }
作者:自为风月马前卒
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


