洛谷P2704 [NOI2001]炮兵阵地(状压dp)

题目描述

司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成，地图的每一格可能是山地（用“H” 表示），也可能是平原（用“P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

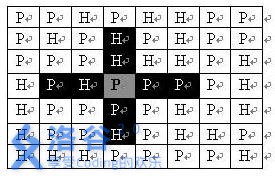
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入输出格式

输入格式：

 

第一行包含两个由空格分割开的正整数，分别表示N和M；

接下来的N行，每一行含有连续的M个字符（‘P’或者‘H’），中间没有空格。按顺序表示地图中每一行的数据。N≤100；M≤10。

 

输出格式：

 

仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。

 

输入输出样例

输入样例#1： 复制

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

输出样例#1： 复制

6

 

 

这题好恶心啊。。

看到$M <= 10$一眼状压dp

考虑到每个点能影响三行，于是设$f[i][nxt][now]$表示下一行的状态为$nxt$，本行的状态为$now$的答案

转移的时候枚举下一行。

但是这样是$2^{3m}*N$的，然而根据题目要求，实际上我们能枚举到的状态非常有限。

加点剪枝就A啦

 

#include<cstdio>
#include<vector>
#include<algorithm>
#include<cstring>
#include<map>
#include<cmath>
using namespace std;
const int MAXN = 1e5 + 10, INF = 1e9 + 10, B = 31;
inline int read() {
    char c = getchar(); int x = 0, f = 1;
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * f;
}
int N, M;
char s[101][11]; 
int sta[101], f[2][1 << 11][1 << 11];
bool pd(int now) {
    if((now & (now << 1))
     ||(now & (now << 2))
     ||(now & (now >> 1))
     ||(now & (now >> 2)))
        return 1;
    return 0;
}
main() {
#ifdef WIN32
    freopen("a.in", "r", stdin);
#endif 
    N = read(); M = read();
    for(int i = 1; i <= N; i++) {
        scanf("%s", s[i] + 1);
        for(int j = 1; j <= M; j++) 
            if(s[i][j] == 'H')
                sta[i] += 1 << (j - 1);
    }
    
    int limit = (1 << M) - 1, cur = 0, ans = 0;
    for(int i = 0; i <= N; i++, cur ^= 1) {
        for(int now = 0; now <= limit; now++) {
            if(pd(now) || (now & sta[i])) continue;
            for(int pre = 0; pre <= limit; pre++) { 
                if(pd(pre) || (now & pre) || (pre & sta[i - 1])) continue;
                for(int nxt = 0; nxt <= limit; nxt++) {
                    if(pd(nxt) || (now & nxt) || (pre & nxt) || (nxt & sta[i + 1])) continue;
                    f[cur ^ 1][nxt][now] = max(f[cur ^ 1][nxt][now], f[cur][now][pre] + __builtin_popcount(nxt));    
                    if(i == N - 1) ans = max(ans, f[cur ^ 1][nxt][now]);
                //    printf("%d %d %d %d\n", i, nxt, now, f[cur ^ 1][nxt][now]);
                }
            }
        }
    }
    printf("%d", ans);
    return 0;
}