计算几何笔记

 

本文中所有图片及其他引用均已获得原作者同意

向量

常规操作

struct Vector {
    double x, y;
    Vector(double x = 0, double y = 0) : x(x), y(y) {};
    Vector operator + (const Vector &A) const {
        return Vector(x + A.x, y + A.y);
    }//向量的加法 
    Vector operator - (const Vector &A) const {
        return Vector(x - A.x, y - A.y);
    }//减法 
    Vector operator * (const double &A) const {
        return Vector(x * A, y * A);
    }//数乘 
    Vector operator / (const double &A) const {
        return Vector(x / A, y / A);
    }//数除 
    bool operator == (const Vector &A) const  {
        return dcmp(x - A.x) == 0 && dcmp(y - A.y) == 0;
    }//相等 
};

向量的极角

极角：这里指从$x$轴旋转到向量方向的弧度

double PolarAngle(Vector A) {
    return atan2(A.y, A.x);
}//向量的极角 

向量的旋转

若向量$(x, y)$旋转角度为$a$，则旋转后的向量为$(xcosa - ysina, y cosa + xsina)$

证明：

设旋转之前的向量的极角为$t$，半径为$r$

那么

$$x = rcost$$

$$y = rsint$$

旋转时候的向量为

$$x' = rcos(t + a) = r(costcosa - sintsina) = xcosa - ysina$$

$$y' = rsin(t + a) = r(sintcosa + costsina) = ycosa + xsina$$

Vector rotate(Vector &A, double a) {
    return A = Vector(A.x * cos(a) - A.y * sin(a), A.x * sin(a) + A.y * cos(a));
}//向量旋转，a为弧度 

向量的点积

$a \cdot b = |a||b|cos<a,b>$

两向量的点积得到的是标量，即一个向量的模长乘另一个向量在该向量上正投影的数量

double Dot(Vector A, Vector B) {
    return A.x * B.x +  A.y * B.y;
}//两向量点积 

向量的叉积

$a \times b = |a||b| sin<a,b>$

两向量叉积得到的是向量，在二维平面中得到的是三维空间中与这两个向量垂直的向量

在平面中，向量$v$和$w$的叉积等于$v$和$w$组成的三角形的有向面积的两倍

记$cross(v,w)$表示两向量的叉积，若$cross(v,w) > 0 $则说明$w$在$v$的左侧，否则$w$在$v$的右侧

double Cross(Vector A, Vector B) {
    return A.x * B.y - A.y * B.x; 
}//两向量叉积 

计算三角形面积

直接利用叉积的定义

double Area(Point A, Point B, Point C) {
    return fabs(Cross(B - A, C - A) / 2);
}//计算三角形的面积 

计算向量的长度

直接利用点积的定义

double Length(Vector A) {
    return sqrt(Dot(A, A));
}//计算向量的长度 

计算向量的夹角

同样直接利用点积的定义

double Angle(Vector A, Vector B) {
    return acos(Dot(A, B) / Length(A) / Length(B));
}//计算向量的夹角 

线段

判断两直线的相对位置

判断$P_1P_0$与$P_1P_2$的相对位置关系，可以转化为判断$P_1P_0$与$P_2P_0$叉积的正负性

int Direction(Vector P1, Vector P2, Vector P0) {
    int opt = Cross(P1 - P0, P2 - P0);
    return dcmp(opt);
}//判断P1-P0,P1-P2的相对位置关系，-1为逆时针，1为顺时针(P1P0顺时针旋转到P1P2)，0为共线 

判断两直线的交点

尼玛看不懂

Point GetLineIntersection(Point P, Vector V, Point Q, Vector W) {
    Vector u = P - Q;
    double t = Cross(W, u) / Cross(V, W);
    return P + V * t;
}//判断两直线(P + tv,Q + tW)的交点(看不懂直接上y = kx + b吧) 

计算点到直线的距离

利用叉积算出他们围城的平行四边形的面积，再除以底，高即为距离

double DistanceToLine(Point P, Point A, Point B) {
    Vector v1 = B - A, v2 = P - A;
    return fabs(Cross(v1, v2)) / Length(v1);
}//计算点P到直线AB的距离（平行四边形面积 / 底）

计算点到线段的距离

这个要分三种情况讨论

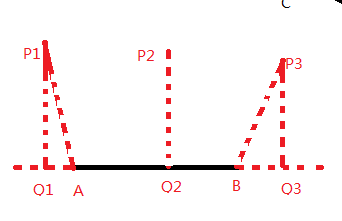
double DistanceToSegment(Point P, Point A, Point B) {
    if(A == B) return Length(P - A);
    if(dcmp(Dot(P - A, B - A)) < 0) return Length(P - A);
    if(dcmp(Dot(P - B, A - B)) < 0) return Length(P - B);
    return DistanceToLine(P, A, B);
}//计算点P到线段AB的距离 

 

多边形

计算外接圆的圆心

某次考试遇到的

    double x1, x2, x3, y1, y2, y3;
    x1  =  p[a].x;
    x2  =  p[b].x;
    x3  =  p[c].x;
    y1  =  p[a].y;
    y2  =  p[b].y;
    y3  =  p[c].y;
    //求外接圆圆心
    double t1 = x1 * x1 + y1 * y1;
    double t2 = x2 * x2 + y2 * y2;
    double t3 = x3 * x3 + y3 * y3;
    double temp = x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2;
    double x = (t2 * y3 + t1 * y2 + t3 * y1 - t2 * y1 - t3 * y2 - t1 * y3) / temp / 2;
    double y = (t3 * x2 + t2 * x1 + t1 * x3 - t1 * x2 - t2 * x3 - t3 * x1) / temp / 2;
    Point ma;//中点 
    ma.x = x;
    ma.y = y;

 

计算多边形的有向面积

将$n$边形拆成三角形

double PolygonAread(Point *P, int N) {
    double area = 0;
    for(int i = 1; i <= N - 1; i++) 
        area += Cross(P[i] - P[0], P[i + 1] - P[0]);
    return area / 2;
}//计算多边形的有向面积

判断点是否在多边形内部

基本思想：从点$P$向右做一条射线，判断从无限远处到点$P$，射线穿过了几条边

有两种需要特判的情况

1.射线与某条边重合，该边不统计入答案

2.射线与端点重合

此时，我们钦定边是由编号小的连向编号大的

若边从上到下穿过了射线，包含终点不包含起点

若边从下到上穿过了射线，包含起点不包含重点

int isPointInPolygon(Point P, Point Poly[], int N) {
    int wn = 0, k, d1, d2;
    for(int i = 0; i < N; i++) {
        if(!dcmp(DistanceToSegment(P, Poly[i], Poly[(i + 1) % N]))) return -1;
    //点在线段的边界上
        k = dcmp(Cross(Poly[(i + 1) % N] - Poly[i], P - Poly[i]));
        d1 = dcmp(Poly[i].y - P.y);
        d2 = dcmp(Poly[(i + 1) % N].y - P.y);
        if(k > 0 && d1 <= 0 && d2 > 0) wn++;//点在左，下上穿
        if(k > 0 && d2 <= 0 && d1 > 0) wn++;//点在右，上下穿
        return wn & 1; // 1：内 2：外    
    }    
}//判断点是否在多边形内部

 

对踵点

定义：若点对$(a, b)$均为多边形上的点且存在过$a$点的切线与过$b$点的切线平行，则成$(a, b)$为多边形上的对踵点

计算方法：

设$p_{ymin}$表示$y$最小的点，$q_{ymax}$表示$y$最大的点，显然它们是一对对踵点

接下来以相同的角速度逆时针旋转两条射线，当其中的一条穿过多边形的下一个端点$p_{next}$时，用$p_{next}$作为新的端点，同时与$q_{pre}$构成新的对踵点。

在这个算法中，我们快速的找出两条射线究竟是哪条先穿过下一个端点，我们可以用叉积来优化这一过程。

 

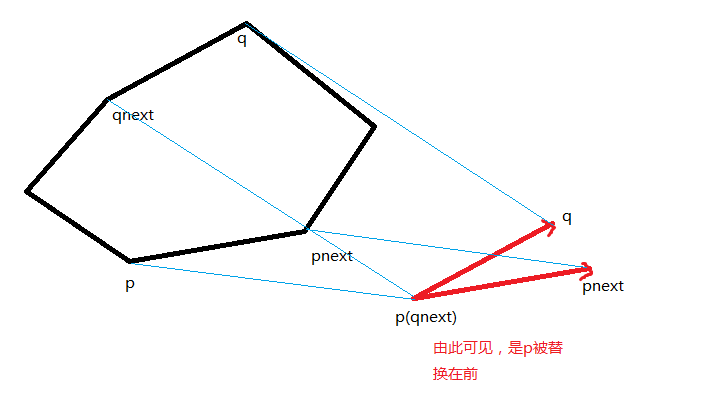
求凸多边形的直径

定义：凸多边形的直径为多边形的上最远的点对的距离

很显然，直径一定是在对踵点处取得，直接枚举对踵点即可

double RotatingCaliper_diameter(Point Poly[], int N) {
    int p = 0, q = N - 1, fl;
    double ret = 0;
    for(int i = 0; i < N; i++) {
        if(Poly[i].y > Poly[q].y) q = i;
        if(Poly[i].y < Poly[p].y) p = i;
    }
    for(int i = 0; i < N * 3; i++) {
        ret = max(ret, Length(Poly[p % N] - Poly[q % N]));
        fl = dcmp(Cross(Poly[(p + 1) % N] - Poly[p % N], Poly[q % N] - Poly[(q + 1) % N]));
        if(!fl) {
            ret = max(ret, Length(Poly[p % N] - Poly[(q + 1) % N]));
            ret = max(ret, Length(Poly[q % N] - Poly[(p + 1) % N]));
            p++, q++;
        } else {
            if(fl > 0) p++;
            else q++;
        }
    }
}//计算多边形直径 

 

凸多边形的宽度

凸多边形最小面积外接矩形

凸包-Andrew算法

首先按照$x$为第一关键字，$y$为第二关键字从小到大排序，并删除重复的点

用栈维护凸包内的点

1、把$p_1, p_2$放入栈中

2、若$p_{i{(i > 3)}}$在直线$p_{i - 1}, p_{i - 2}$的右侧，则不断的弹出栈顶，直到该点在直线左侧

3、此时我们已经得到了下凸包，那么反过来从$p_n$再做一次即可得到下凸包

题目链接

// luogu-judger-enable-o2
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int eps = 1e-10;
int dcmp(double x) {
    if(fabs(x) < eps) return 0;
    return x < 0 ? -1 : 1;
}
#define Point Vector 
struct Vector {
    double x, y;
    Vector(double x = 0, double y = 0) : x(x), y(y) {};
    bool operator < (const Vector &rhs) const {
        return dcmp(x - rhs.x) == 0 ? y < rhs.y : x < rhs.x;
    }
    Vector operator - (const Vector &rhs) const {
        return Vector(x - rhs.x, y - rhs.y);
    }
};
double Cross(Vector A, Vector B) {
    return A.x * B.y - A.y * B.x; 
}
double dis(Point a, Point b) {
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
int N; 
Point p[10001], q[10001];
int top;
void Push(Point p) {
    while(Cross(q[top] - q[top - 1], p - q[top - 1]) < 0) top--;
    q[++top] = p;
}
void Andrew() {
    q[0] = q[top = 1] = p[1];
    for(int i = 2; i <= N; i++) Push(p[i]);
    for(int i = N - 1; i; --i)  Push(p[i]);
}
int main() {    
    scanf("%d", &N);
    for(int i = 1; i <= N; i++) scanf("%lf%lf", &p[i].x, &p[i].y);
    sort(p + 1, p + N + 1);
    Andrew();
    double ans = 0;
    for(int i = 1; i < top; i++)
        ans += dis(q[i], q[i + 1]);
    printf("%.2lf", ans);
    return 0;
}

 

 

 

 

 

要做的题

POJ 2187 凸多边形直径

 

 

 

#include<cstdio>
#include<cmath>
using namespace std;
const int eps = 1e-10;
int dcmp(double x) {
    if(fabs(x) < eps) return 0;
    return x < 0 ? -1 : 1;
}
#define Point Vector 
struct Vector {
    double x, y;
    Vector(double x = 0, double y = 0) : x(x), y(y) {};
    Vector operator + (const Vector &A) const {
        return Vector(x + A.x, y + A.y);
    }//向量的加法 
    Vector operator - (const Vector &A) const {
        return Vector(x - A.x, y - A.y);
    }//减法 
    Vector operator * (const double &A) const {
        return Vector(x * A, y * A);
    }//数乘 
    Vector operator / (const double &A) const {
        return Vector(x / A, y / A);
    }//数除 
    bool operator == (const Vector &A) const  {
        return dcmp(x - A.x) == 0 && dcmp(y - A.y) == 0;
    }//相等 
};
double PolarAngle(Vector A) {
    return atan2(A.y, A.x);
}//向量的极角 
Vector rotate(Vector &A, double a) {
    return A = Vector(A.x * cos(a) - A.y * sin(a), A.x * sin(a) + A.y * cos(a));
}//向量旋转，a为弧度 
double Dot(Vector A, Vector B) {
    return A.x * B.x +  A.y * B.y;
}//两向量点积 
double Cross(Vector A, Vector B) {
    return A.x * B.y - A.y * B.x; 
}//两向量叉积 
double Area(Point A, Point B, Point C) {
    return fabs(Cross(B - A, C - A) / 2);
}//计算三角形的面积 
double Length(Vector A) {
    return sqrt(Dot(A, A));
}//计算向量的长度 
double Angle(Vector A, Vector B) {
    return acos(Dot(A, B) / Length(A) / Length(B));
}//计算向量的夹角 
int Direction(Vector P1, Vector P2, Vector P0) {
    int opt = Cross(P1 - P0, P2 - P0);
    return dcmp(opt);
}//判断P1-P0,P1-P2的相对位置关系，-1为逆时针，1为顺时针(P1P0顺时针旋转到P1P2)，0为共线 
Point GetLineIntersection(Point P, Vector V, Point Q, Vector W) {
    Vector u = P - Q;
    double t = Cross(W, u) / Cross(V, W);
    return P + V * t;
}//判断两直线(P + tv,Q + tW)的交点(看不懂直接上y = kx + b吧) 
double DistanceToLine(Point P, Point A, Point B) {
    Vector v1 = B - A, v2 = P - A;
    return fabs(Cross(v1, v2)) / Length(v1);
}//计算点P到直线AB的距离（平行四边形面积 / 底）
double DistanceToSegment(Point P, Point A, Point B) {
    if(A == B) return Length(P - A);
    if(dcmp(Dot(P - A, B - A)) < 0) return Length(P - A);
    if(dcmp(Dot(P - B, A - B)) < 0) return Length(P - B);
    return DistanceToLine(P, A, B);
}//计算点P到线段AB的距离
double PolygonAread(Point *P, int N) {
    double area = 0;
    for(int i = 1; i <= N - 1; i++) 
        area += Cross(P[i] - P[0], P[i + 1] - P[0]);
    return area / 2;
}//计算多边形的有向面积
int isPointInPolygon(Point P, Point Poly[], int N) {
    int wn = 0, k, d1, d2;
    for(int i = 0; i < N; i++) {
        if(!dcmp(DistanceToSegment(P, Poly[i], Poly[(i + 1) % N]))) return -1;
    //点在线段的边界上
        k = dcmp(Cross(Poly[(i + 1) % N] - Poly[i], P - Poly[i]));
        d1 = dcmp(Poly[i].y - P.y);
        d2 = dcmp(Poly[(i + 1) % N].y - P.y);
        if(k > 0 && d1 <= 0 && d2 > 0) wn++;//点在左，下上穿
        if(k > 0 && d2 <= 0 && d1 > 0) wn++;//点在右，上下穿
        return wn & 1; // 1：内 2：外    
    }    
}//判断点是否在多边形内部

int main() {    
        
    return 0;
}

 

 

参考资料

也许是史上最不良心的低阶计算几何讲解和习题集？？