树上莫队算法

简介

树上莫队，顾名思义就是把莫队搬到树上。

我们从一道题目入手[SDOI2018]原题识别 SPOJ Count on a tree II

题目意思很明确：给定一个$n$个节点的树，每个节点表示一个整数，问$u$到$v$的路径上有多少个不同的整数。

像这种不带修改数颜色的题首先想到的肯定是树套树莫队，那么如何把在序列上的莫队搬到树上呢？

算法

欧拉序

我们考虑用什么东西可以把树上的问题转化到序列上，dfs序是可以的，但是这道题不行（无法搞lca的贡献）

有一种神奇的东西，叫做欧拉序。

它的核心思想是：当访问到点$i$时，加入序列，然后访问$i$的子树，当访问完时，再把$i$加入序列

煮个栗子，下面这棵树的欧拉序为

$1\ 2\ 3\ 4\ 4\ 5\ 5\ 6\ 6\ 3\ 7\ 7\ 2\ 1$

 

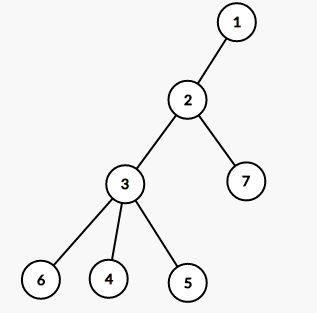
树上莫队

有了这个有什么用呢？

我们考虑我们要解决的问题：求$x$到$y$的路径上有多少个不同的整数

 

这里我们设$st[i]$表示访问到$i$时加入欧拉序的时间，$ed[i]$表示回溯经过$i$时加入欧拉序的时间

不妨设$st[x]<st[y]$（也就是先访问$x$，再访问$y$）

分情况讨论 

 

若$lca(x,y) = x$，这时$x,y$在一条链上，那么$st[x]$到$st[y]$这段区间中，有的点出现了两次，有的点没有出现过，这些点都是对答案没有贡献的，我们只需要统计出现过$1$次的点就好

比如当询问为$2,6$时，$(st[2],st[6])=2\ 3\ 4\ 4\ 5\ 5\ 6$，$4,5$这两个点都出现了两次，因此不统计进入答案

若$lca(x,y) \not = x$，此时$x,y$位于不同的子树内，我们只需要按照上面的方法统计$ed[x]$到$st[y]$这段区间内的点。 

比如当询问为$4,7$时，$(ed[4],st[7]) = 4\ 5\ 5\ 6\ 6\ 3\ 7\ $。大家发现了什么？没错！我们没有统计$lca$，因此我们需要特判$lca$

 

然后就没啦，开始愉快的调代码吧

 

相关证明

此处纯为作者瞎扯。。。

• 为什么出现两次的点不统计答案

树上路径的定义为：从$x$到$y$经过节点个数最少的路径。

若一个点$k$出现两次，说明我们可以先访问$k$，进入$k$的子树中，然后出来，再到$y$，很显然不访问$k$是更优的。因此出现两次的点不能统计入答案

• 为什么当$lca(x,y) \not =x$时需要从$ed[x]$开始遍历

从$st[x]$到$ed[x]$为$x$的子树中的节点，很显然这些节点不能统计进答案

代码

注意我们询问的区间长度为$2*N$，所以预处理的时候一定要循环到$2*N$！

 

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<vector>
//#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
char buf[1 << 21], *p1 = buf, *p2 = buf;
using namespace std;
const int MAXN = 1e5 + 10;
inline int read() {
    char c = getchar(); int x = 0, f = 1;
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * f;
}
int N, Q;
int belong[MAXN], block;
struct Query {
    int l, r, ID, lca, ans;
    bool operator < (const Query &rhs) const{
        return belong[l] == belong[rhs.l] ? r < rhs.r : belong[l] < belong[rhs.l];
    //    return belong[l] < belong[rhs.l];
    }
}q[MAXN];
vector<int>v[MAXN];
int a[MAXN], date[MAXN];
void Discretization() {
    sort(date + 1, date + N + 1);
    int num = unique(date + 1, date + N + 1) - date - 1;
    for(int i = 1; i <= N; i++) a[i] = lower_bound(date + 1, date + num + 1, a[i]) - date;    
}
int deep[MAXN], top[MAXN], fa[MAXN], siz[MAXN], son[MAXN], st[MAXN], ed[MAXN], pot[MAXN], tot;
void dfs1(int x, int _fa) {
    fa[x] = _fa; siz[x] = 1;
    st[x] = ++ tot; pot[tot] = x; 
    for(int i = 0; i < v[x].size(); i++) {
        int to = v[x][i];
        if(deep[to]) continue;
        deep[to] = deep[x] + 1;
        dfs1(to, x);
        siz[x] += siz[to];
        if(siz[to] > siz[son[x]]) son[x] = to;
    }
    ed[x] = ++tot; pot[tot] = x;
}
void dfs2(int x, int topfa) {
    top[x] = topfa;
    if(!son[x]) return ;
    dfs2(son[x], topfa);
    for(int i = 0; i < v[x].size(); i++) {
        int to = v[x][i];
        if(top[to]) continue;
            dfs2(to, to);
    }
}
int GetLca(int x, int y) {
    while(top[x] != top[y]) {
        if(deep[top[x]] < deep[top[y]]) swap(x, y);
        x = fa[top[x]];
    }
    return deep[x] < deep[y] ? x : y;
}
void DealAsk() {
    for(int i = 1; i <= Q; i++) {
        int x = read(), y = read();
        if(st[x] > st[y]) swap(x, y);
        int _lca = GetLca(x, y);
        q[i].ID = i;
        if(_lca == x) q[i].l = st[x], q[i]. r = st[y];
        else q[i].l = ed[x], q[i].r = st[y], q[i].lca = _lca;
    }
}
int Ans, out[MAXN], used[MAXN], happen[MAXN];
void add(int x) {
    if(++happen[x] == 1) Ans++;
}
void delet(int x) {
    if(--happen[x] == 0) Ans--;
}
void Add(int x) {
    used[x] ? delet(a[x]) : add(a[x]); used[x] ^= 1;
}
void Mo() {
    sort(q + 1, q + Q + 1);
    int l = 1, r = 0, fuck = 0;
    for(int i = 1; i <= Q; i++) {
        while(l < q[i].l) Add(pot[l]), l++, fuck++;
        while(l > q[i].l) l--, Add(pot[l]), fuck++;
        while(r < q[i].r) r++, Add(pot[r]), fuck++;
        while(r > q[i].r) Add(pot[r]), r--, fuck++;
        if(q[i].lca) Add(q[i].lca);
        q[i].ans = Ans;
        if(q[i].lca) Add(q[i].lca);
    }
    for(int i = 1; i <= Q; i++) out[q[i].ID] = q[i].ans;
    for(int i = 1; i <= Q; i++)
        printf("%d\n", out[i]);
}
int main() {
    N = read(); Q = read();
    //block = 1.5 * sqrt(2 * N) + 1;
    //block = pow(N, 0.66666666666);
    block = sqrt(N);
    for(int i = 1; i <= N; i++) a[i] = date[i] = read();
    for(int i = 1; i <= N * 2; i++) belong[i] = i / block + 1;
    Discretization();
    for(int i = 1; i <= N - 1; i++) {
        int x = read(), y = read();
        v[x].push_back(y); v[y].push_back(x);
    }
    deep[1] = 1; dfs1(1, 0);
    dfs2(1, 1);
/*    for(int i = 1; i <= N; i++)    
        for(int j = 1; j <= i - 1; j++)
            printf("%d %d %d\n", i, j, GetLca(i, j));*/
    DealAsk();
    Mo();
    return 0;
}