BZOJ1007: [HNOI2008]水平可见直线(单调栈)
Submit: 8638 Solved: 3327
[Submit][Status][Discuss]
Description
在xoy直角坐标平面上有n条直线L1,L2,...Ln,若在y值为正无穷大处往下看,能见到Li的某个子线段,则称Li为
可见的,否则Li为被覆盖的.
例如,对于直线:
L1:y=x; L2:y=-x; L3:y=0
则L1和L2是可见的,L3是被覆盖的.
给出n条直线,表示成y=Ax+B的形式(|A|,|B|<=500000),且n条直线两两不重合.求出所有可见的直线.
Input
第一行为N(0 < N < 50000),接下来的N行输入Ai,Bi
Output
从小到大输出可见直线的编号,两两中间用空格隔开,最后一个数字后面也必须有个空格
Sample Input
3
-1 0
1 0
0 0
-1 0
1 0
0 0
Sample Output
1 2
HINT
Source
我的思路:
对于一条直线,如果看不见,有且仅有两种情况
一:被一条斜率相同,但是$b$比它大的直线遮挡住
二:被两条交叉的直线遮挡住,也就是下面这种情况
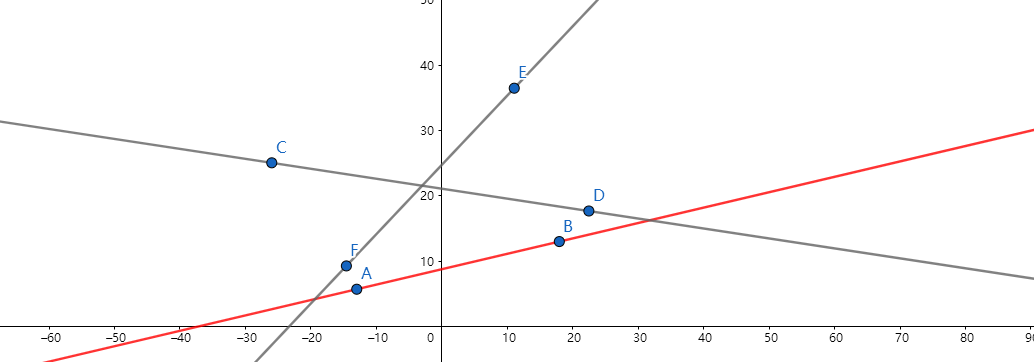
对于第一种情况,直接判断即可
对于第二种情况,直接处理有一些麻烦,所以我们考虑首先按照斜率从小到大排序
同时维护一个栈
如果当前直线与栈顶元素的前一个元素的交点 比 栈顶元素和栈顶前一个元素的交点 的横坐标 靠左,那么栈顶的前一个元素就没用了
最后统计栈中有哪些元素就可以
有点类似于单调栈
时间复杂度:$O(n)$
#include<cstdio> #include<algorithm> #include<cmath> using namespace std; const int MAXN = 200001; const double eps = 1e-7; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();} while(c >= '0' && c <= '9') {x = x * 10 + c - '0';c = getchar();} return x * f; } int N; struct Seg { int ID; double k, b; bool operator < (const Seg &rhs) const { return fabs(k - rhs.k) <= eps ? b < rhs.b : k < rhs.k; } }a[MAXN], S[MAXN]; int top = 0; int Ans[MAXN]; double X(Seg x, Seg y) { return (y.b - x.b) / (x.k - y.k); } void Solve() { fill(Ans + 1, Ans + N + 1, 1); S[++top] = a[1]; for(int i = 2; i <= N; i++) { while( ( fabs(a[i].k - S[top].k) <= eps) || (top > 1 && X(a[i], S[top - 1]) <= X(S[top - 1], S[top]))) Ans[S[top].ID] = 0, top--; S[++top] = a[i]; } } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #else //freopen("bzoj_1007.in","r",stdin); //freopen("bzoj_1007.out","w",stdout); #endif N = read(); for(int i = 1; i <= N; i++) a[i].k = read(), a[i].b = read(), a[i].ID = i; sort(a + 1, a + N + 1); Solve(); for(int i = 1; i <= N; i++) if(Ans[i] == 1) printf("%d ",i); return 0; }
作者:自为风月马前卒
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


