BZOJ1101: [POI2007]Zap(莫比乌斯反演)
1101: [POI2007]Zap
Time Limit: 10 Sec Memory Limit: 162 MBSubmit: 2951 Solved: 1293
[Submit][Status][Discuss]
Description
FGD正在破解一段密码,他需要回答很多类似的问题:对于给定的整数a,b和d,有多少正整数对x,y,满足x<=a
,y<=b,并且gcd(x,y)=d。作为FGD的同学,FGD希望得到你的帮助。
Input
第一行包含一个正整数n,表示一共有n组询问。(1<=n<= 50000)接下来n行,每行表示一个询问,每行三个
正整数,分别为a,b,d。(1<=d<=a,b<=50000)
Output
对于每组询问,输出到输出文件zap.out一个正整数,表示满足条件的整数对数。
Sample Input
2
4 5 2
6 4 3
4 5 2
6 4 3
Sample Output
3
2
//对于第一组询问,满足条件的整数对有(2,2),(2,4),(4,2)。对于第二组询问,满足条件的整数对有(
6,3),(3,3)。
2
//对于第一组询问,满足条件的整数对有(2,2),(2,4),(4,2)。对于第二组询问,满足条件的整数对有(
6,3),(3,3)。
HINT
Source
莫比乌斯反演裸题
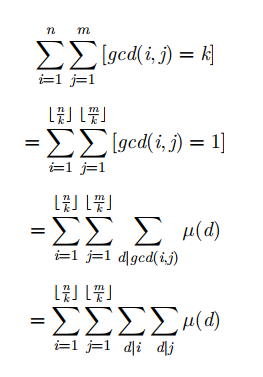
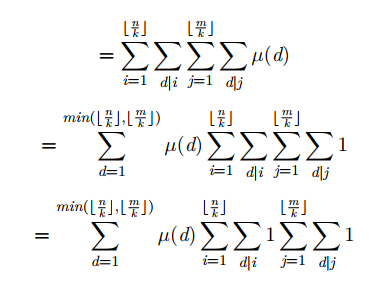
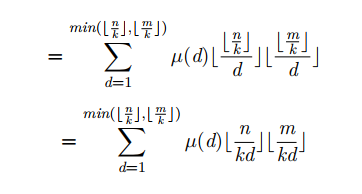
$\frac{n}{k}$只有$sqrt(n)$个取值
所以可以用分块优化
#include<cstdio> #include<cstring> #include<cmath> #include<algorithm> using namespace std; const int MAXN=1e6+10; inline int read() { char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int N; int vis[MAXN]; long long prime[MAXN],mu[MAXN],tot=0; void GetMu() { vis[1]=1;mu[1]=1; for(int i=1;i<=N;i++) { if(!vis[i]) prime[++tot]=i,mu[i]=-1; for(int j=1;j<=tot&&i*prime[j]<=N;j++) { vis[i*prime[j]]=1; if(i%prime[j]==0) {mu[i*prime[j]]=0;break;} else mu[i*prime[j]]=-mu[i]; } } for(int i=1;i<=N;i++) mu[i]+=mu[i-1]; } main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif N=1e5; GetMu(); int QWQ=read(); while(QWQ--) { int n=read(),m=read(),k=read(); long long ans=0; int limit=min(n/k,m/k); int nxt=0; for(int i=1;i<=limit;i=nxt+1) nxt=min(n/(n/i),m/(m/i)), ans+=(mu[nxt]-mu[i-1])*((n/k)/i)*((m/k)/i); printf("%lld\n",ans); } return 0; }
作者:自为风月马前卒
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


