博弈论进阶之树的删边游戏与无向图的删边游戏

PS:本文内容大部分借(chao)鉴(xo)自yhqz

树的删边游戏

给出一个有 N个点的树，有一个点作为树的根节点。游戏者轮流从树中删去边，删去一条边后，不与根节点相连的部分将被移走。谁无法移动谁输。

结论

叶子节点的SG值为0；中间节点的SG值为它的所有子节点的SG值加1后的异或和。

证明

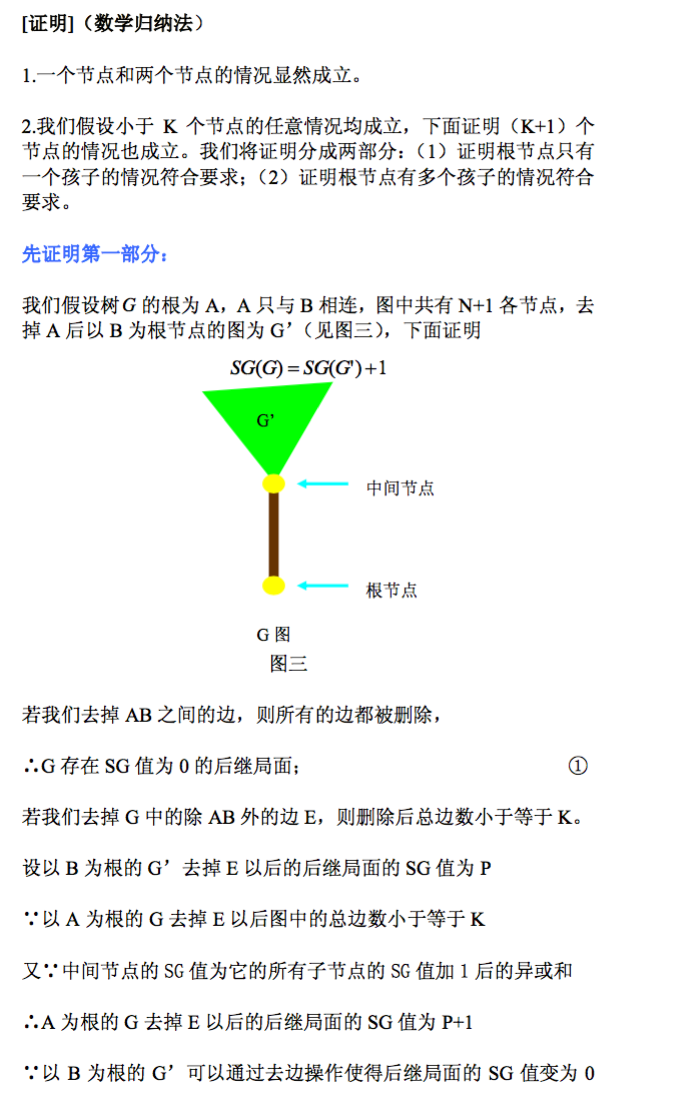
无向图的删边游戏

一个无相联通图，有一个点作为图的根。

游戏者轮流从图中删去边，删去一条边后，不与根节点相连的部分将被移走。

谁无路可走谁输。

结论

对于这个模型，有一个著名的定理——Fusion Principle

我们可以对无向图做如下改动：将图中的任意一个偶环缩成一个新点，任意一个奇环缩成一个新点加一个新边；所有连到原先环上的边全部改为与新点相连。这样的改动不会影响图的SG 值。

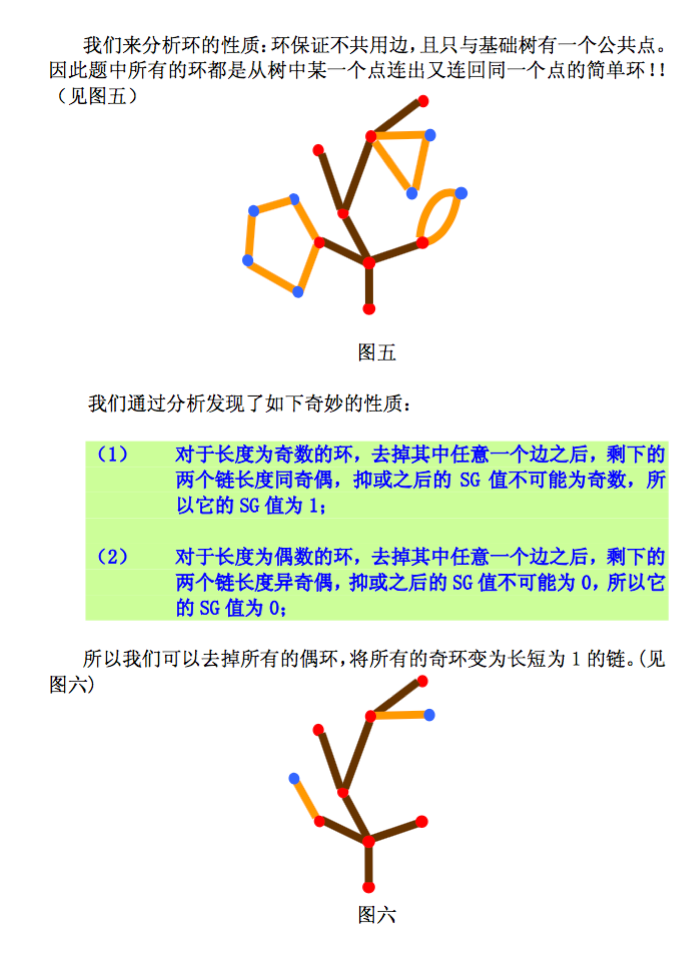
这样的话，我们可以将任意一个无向图改成树结构，“无向图的删边游戏”就变成了“树的删边游戏”。