洛谷P3355 骑士共存问题

题目描述

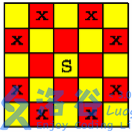
在一个 n*n个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入

　　

对于给定的 n*n 个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击

输入输出格式

输入格式：

 

第一行有 2 个正整数n 和 m (1<=n<=200, 0<=m<n2)，分别表示棋盘的大小和障碍数。接下来的 m 行给出障碍的位置。每行 2 个正整数，表示障碍的方格坐标。

 

输出格式：

 

将计算出的共存骑士数输出

 

输入输出样例

输入样例#1： 复制

3 2
1 1
3 3

输出样例#1： 复制

5 

 

最大流与最小割之间的转换

最多放多少骑士==最少拿走多少

观察图片不难发现：黄色的不能攻击黄色的，红色同理

那么不难想到二分图匹配

这样就转化成了二分图最小定点覆盖

而二分图最小顶点覆盖==二分图最大匹配。证明可以看[这里](http://www.cnblogs.com/jianglangcaijin/p/6035945.html)

从S向红色连边（权重为1），从红色向能攻击到的黄色连边（权重为INF），从黄色向T连边（权重为1）

 

// luogu-judger-enable-o2
#include<cstdio>
#include<cstring>
#include<queue>
#define AddEdge(x,y,z) add_edge(x,y,z),add_edge(y,x,0);
using namespace std;
const int MAXN=100001,INF=1e8+10;
inline char nc()
{
    static char buf[MAXN],*p1=buf,*p2=buf;
    return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin),p1==p2)?EOF:*p1++;
}
inline int read()
{
    char c=nc();int x=0,f=1;
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=nc();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=nc();}
    return x*f;
}
int N,M,S,T;
struct node
{
    int u,v,flow,nxt;
}edge[MAXN*5];
int head[MAXN],cur[MAXN],num=0;
inline void add_edge(int x,int y,int z)
{
    edge[num].u=x;
    edge[num].v=y;
    edge[num].flow=z;
    edge[num].nxt=head[x];
    head[x]=num++;
}
int deep[MAXN];
inline bool BFS()
{
    memset(deep,0,sizeof(deep));
    deep[S]=1;
    queue<int>q;
    q.push(S);
    while(q.size()!=0)
    {
        int p=q.front();
        q.pop();
        for(int i=head[p];i!=-1;i=edge[i].nxt)
            if(!deep[edge[i].v]&&edge[i].flow)
            {
                deep[edge[i].v]=deep[p]+1;q.push(edge[i].v);
                if(edge[i].v==T) return 1;
            }
    }
    return deep[T];
}
int DFS(int now,int nowflow)
{
    if(now==T||nowflow<=0)    return nowflow;
    int totflow=0;
    for(int &i=cur[now];i!=-1;i=edge[i].nxt) 
    {
        if(deep[edge[i].v]==deep[now]+1&&edge[i].flow)
        {
            int canflow=DFS(edge[i].v,min(nowflow,edge[i].flow));
            edge[i].flow-=canflow;edge[i^1].flow+=canflow;
            totflow+=canflow;
            nowflow-=canflow;
            if(nowflow<=0) break;
        }
    }
    return totflow;
}
int Dinic()
{
    int ans=0;
    while(BFS())
    {
        memcpy(cur,head,sizeof(head)); 
        ans+=DFS(S,INF);
    }
    return ans;    
}
int a[201][201],c[201][201];
int xx[15]={0,-1,-2,-2,-1,+1,+2,+2,+1};
int yy[15]={0,-2,-1,+1,+2,+2,+1,-1,-2};
int main()
{
    #ifdef WIN32
    freopen("a.in","r",stdin);
    #else
    #endif
    memset(head,-1,sizeof(head));
    N=read();M=read();S=0;T=N*N+1;
    for(int i=1;i<=M;i++)
    {
        int x=read(),y=read();
        c[x][y]=1;
    }
    for(int i=1;i<=N;i++)
        for(int j=1;j<=N;j++)
            a[i][j]=(i-1)*N+j;
    for(int i=1;i<=N;i++)
        for(int j=1;j<=N;j++)
        {
            if(c[i][j]) continue;
            if((i+j)%2) 
            {
                AddEdge(S,a[i][j],1);
                for(int k=1;k<=8;k++)
                {
                    int wx=i+xx[k],wy=j+yy[k];
                    if(wx>=1&&wx<=N&&wy>=1&&wy<=N)
                        AddEdge(a[i][j],a[wx][wy],INF);
                }
            }
            else AddEdge(a[i][j],T,1);
        }
    printf("%d",N*N-M-Dinic());
    
    return  0;
}