树链剖分详解
前言
- 树链剖分是什么？
树链剖分，说白了就是一种让你代码不得不强行增加1k的数据结构-dms
个人理解：+1:joy:
- 有什么用？
证明出题人非常毒瘤
可以非常友(bao)好(li)的解决一些树上问题:grimacing:
（友情提示：学树链剖分之前请先掌握线段树）
核心思想
树链剖分的思想比较神奇
它的思想是：把一棵树拆成若干个不相交的链，然后用一些数据结构去维护这些链
那么问题来了
- 如何把树拆成链？
首先明确一些定义
重儿子：该节点的子树中,节点个数最多的子树的根节点(也就是和该节点相连的点)，即为该节点的重儿子
重边：连接该节点与它的重儿子的边
重链：由一系列重边相连得到的链
轻链：由一系列非重边相连得到的链
这样就不难得到拆树的方法
对于每一个节点，找出它的重儿子，那么这棵树就自然而然的被拆成了许多重链与许多轻链
- 如何对这些链进行维护？
首先，要对这些链进行维护，就要确保每个链上的节点都是连续的，
因此我们需要对整棵树进行重新编号，然后利用dfs序的思想，用线段树或树状数组等进行维护（具体用什么需要看题目要求，因为线段树的功能比树状数组强大，所以在这里我就不提供树状数组的写法了）
注意在进行重新编号的时候先访问重链
这样可以保证重链内的节点编号连续
上面说的太抽象了，结合一张图来理解一下
对于一棵最基本的树
给他标记重儿子，
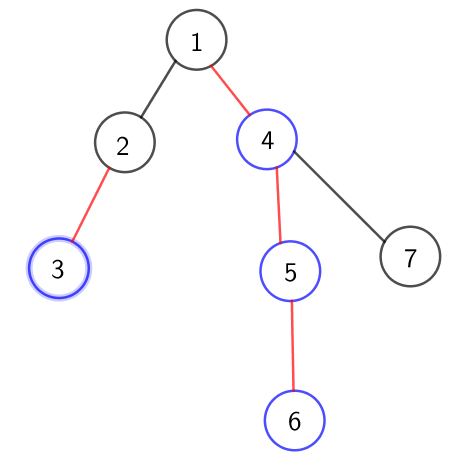蓝色为重儿子，红色为重边
然后对树进行重新编号
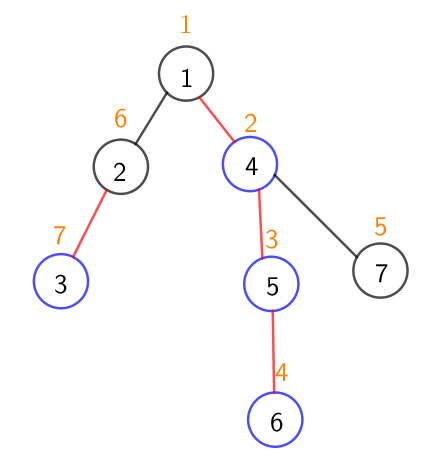橙色表示的是该节点重新编号后的序号
不难看出重链内的节点编号是连续的
然后就可以在线段树上搞事情啦
像什么区间加区间求和什么的
另外有一个性质：以$i$为根的子树的树在线段树上的编号为$[i,i+子树节点数-1]$
接下来结合一道例题，加深一下对于代码的理解
代码
树链剖分的裸题
首先来一坨定义
int deep[MAXN];//节点的深度 int fa[MAXN];//节点的父亲 int son[MAXN];//节点的重儿子 int tot[MAXN];//节点子树的大小
第一步
按照我们上面说的，我们首先要对整棵树dfs一遍，找出每个节点的重儿子
顺便处理出每个节点的深度，以及他们的父亲节点
int dfs1(int now, int f, int dep) { deep[now] = dep; fa[now] = f; tot[now] = 1; int maxson = -1; for (int i = head[now]; i != -1; i = edge[i].nxt) { if (edge[i].v == f) continue; tot[now] += dfs1(edge[i].v, now, dep + 1); if (tot[edge[i].v] > maxson) maxson = tot[edge[i].v], son[now] = edge[i].v; } return tot[now]; }
第二步
然后我们需要对整棵树进行重新编号
我把一开始的每个节点的权值存在了$b$数组内
void dfs2(int now, int topf) { idx[now] = ++cnt; a[cnt] = b[now]; top[now] = topf; if (!son[now]) return ; dfs2(son[now], topf); for (int i = head[now]; i != -1; i = edge[i].nxt) if (!idx[edge[i].v]) dfs2(edge[i].v, edge[i].v); }
$idx$表示重新编号后该节点的编号是多少
另外，这里引入了一个$top$数组，
$top[i]$表示$i$号节点所在重链的头节点(最顶上的节点)
至于这个数组有啥用，后面再说
第三步
我们需要根据重新编完号的树，把这棵树的上每个点映射到线段树上，
struct Tree { int l, r, w, siz, f; } T[MAXN];
void Build(int k, int ll, int rr) { T[k].l = ll; T[k].r = rr; T[k].siz = rr - ll + 1; if (ll == rr) { T[k].w = a[ll]; return ; } int mid = (ll + rr) >> 1; Build(ls, ll, mid); Build(rs, mid + 1, rr); update(k); }
另外线段树的基本操作，
这里就不详细解释了
直接放代码
void update(int k) { //更新 T[k].w = (T[ls].w + T[rs].w + MOD) % MOD; }
void IntervalAdd(int k, int ll, int rr, int val) { //区间加 if (ll <= T[k].l && T[k].r <= rr) { T[k].w += T[k].siz * val; T[k].f += val; return ; } pushdown(k); int mid = (T[k].l + T[k].r) >> 1; if (ll <= mid) IntervalAdd(ls, ll, rr, val); if (rr > mid) IntervalAdd(rs, ll, rr, val); update(k); } int IntervalSum(int k, int ll, int rr) { //区间求和 int ans = 0; if (ll <= T[k].l && T[k].r <= rr) return T[k].w; pushdown(k); int mid = (T[k].l + T[k].r) >> 1; if (ll <= mid) ans = (ans + IntervalSum(ls, ll, rr)) % MOD; if (rr > mid) ans = (ans + IntervalSum(rs, ll, rr)) % MOD; return ans; } void pushdown(int k) { //下传标记 if (!T[k].f) return ; T[ls].w = (T[ls].w + T[ls].siz * T[k].f) % MOD; T[rs].w = (T[rs].w + T[rs].siz * T[k].f) % MOD; T[ls].f = (T[ls].f + T[k].f) % MOD; T[rs].f = (T[rs].f + T[k].f) % MOD; T[k].f = 0; }
第四步
我们考虑如何实现对于树上的操作
树链剖分的思想是:对于两个不在同一重链内的节点,让他们不断地跳,使得他们处于同一重链上
那么如何"跳”呢？
还记得我们在第二次$dfs$中记录的$top$数组么？
有一个显然的结论：$x$到$top[x]$中的节点在线段树上是连续的，
结合$deep$数组
假设两个节点为$x$,$y$
我们每次让$deep[top[x]]$与$deep[top[y]]$中大的(在下面的)往上跳(有点类似于树上倍增)
让x节点直接跳到$top[x]$,然后在线段树上更新
最后两个节点一定是处于同一条重链的，前面我们提到过重链上的节点都是连续的，直接在线段树上进行一次查询就好
void TreeSum(int x, int y) { //x与y路径上的和 int ans = 0; while (top[x] != top[y]) { if (deep[top[x]] < deep[top[y]]) swap(x, y); ans = (ans + IntervalSum(1, idx[ top[x] ], idx[x])) % MOD; x = fa[ top[x] ]; } if (deep[x] > deep[y]) swap(x, y); ans = (ans + IntervalSum(1, idx[x], idx[y])) % MOD; printf("%d\n", ans); } void TreeAdd(int x, int y, int val) { //对于x,y路径上的点加val的权值 while (top[x] != top[y]) { if (deep[top[x]] < deep[top[y]]) swap(x, y); IntervalAdd(1, idx[ top[x] ], idx[x], val); x = fa[ top[x] ]; } if (deep[x] > deep[y]) swap(x, y); IntervalAdd(1, idx[x], idx[y], val); }
在树上查询的这一步可能有些抽象，我们结合一个例子来理解一下
还是上面那张图，假设我们要查询$3.6$这两个节点的之间的点权合，为了方便理解我们假设每个点的点权都是$1$
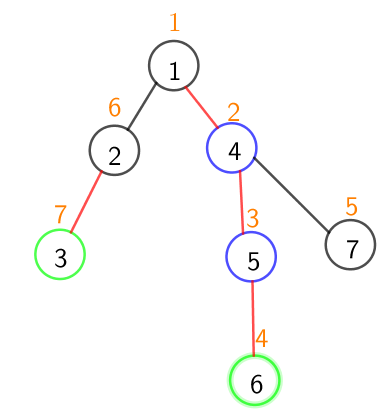
刚开始时
$top[3]=2,top[6]=1$
$deep[top[3]]=2,deep[top[6]]=1$
我们会让$3$向上跳,跳到$top[3]$的爸爸,也就是$1$号节点
这是$1$号节点和$6$号节点已经在同一条重链内,所以直接对线段树进行一次查询即可
对于子树的操作
这个就更简单了
因为一棵树的子树在线段树上是连续的
所以修改的时候直接这样
IntervalAdd(1,idx[x],idx[x]+tot[x]-1,z%MOD);
时间复杂度
(刚开始忘记写了,这一块是后来补上的)
性质1
如果边$\left( u,v\right)$,为轻边,那么$Size\left( v\right) \leq Size\left( u\right) /2$。
证明：显然:joy:，否则该边会成为重边
性质2
树中任意两个节点之间的路径中轻边的条数不会超过$\log _{2}n$,重路径的数目不会超过$\log _{2}n$
证明：不会:stuck_out_tongue_winking_eye:
有了上面两条性质，我们就可以来分析时间复杂度了
由于重路径的数量的上界为$\log _{2}n$，
线段树中查询/修改的复杂度为$\log _{2}n$
那么总的复杂度就是$\left( \log _{2}n\right) ^{2}$
例题
洛谷P3379 【模板】最近公共祖先（LCA）
树剖可以求LCA，没想到吧
http://www.cnblogs.com/zwfymqz/p/8097366.html
洛谷P2590 [ZJOI2008]树的统计
http://www.cnblogs.com/zwfymqz/p/7157156.html
这份代码是以前写的，可能比较丑，下面两份是刚刚写的
洛谷P3178 [HAOI2015]树上操作
http://www.cnblogs.com/zwfymqz/p/8094286.html
洛谷P3038 [USACO11DEC]牧草种植Grass Planting
有点意思
