让priority_queue支持小根堆的几种方法

点击这里了解什么是priority_queue  

前言

priority_queue默认是大根堆，也就是大的元素会放在前面

例如

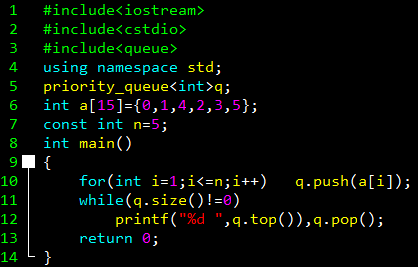
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
priority_queue<int>q;
int a[15]={0,1,4,2,3,5};
const int n=5;
int main()
{
    for(int i=1;i<=n;i++)    q.push(a[i]);
    while(q.size()!=0)
        printf("%d ",q.top()),q.pop();
    return 0;
}

 

　　

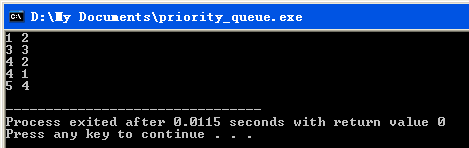
它的输出结果是

那如何让priority_queue支持小根堆呢？:question:

 

方法一

将所有的数全部取负

这样的话绝对值小的数会变大，绝对值大的数会变小

这样就能实现小根堆了

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
priority_queue<int>q;
int a[15]={0,1,4,2,3,5};
const int n=5;
int main()
{
    for(int i=1;i<=n;i++)    q.push(-a[i]);
    while(q.size()!=0)
        printf("%d ",-q.top()),q.pop();
    return 0;
}

 

 

 

方法二

利用STL中自带的小根堆，很简单，只要在定义的时候写成

 就好

 

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
priority_queue<int,vector<int>,greater<int> >q;//这样就可以实现小根堆了 
int a[15]={0,1,4,2,3,5};
const int n=5;
int main()
{
    for(int i=1;i<=n;i++)    q.push(a[i]);
    while(q.size()!=0)
        printf("%d ",q.top()),q.pop();
    return 0;
}

 

 

 

另外

priority_queue是支持自定义比较函数的

 

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int n=5;
struct node
{
    int x,y;
    node(){x=y=0;}
    node(int a,int b){x=a;y=b;}
};
priority_queue<node>q;
bool operator<(const node &a,const node &b)
{
    if(a.x!=b.x)return a.x>b.x;
    return a.y<b.y;
}
int a[15]={0,1,4,4,3,5};
int b[15]={0,2,1,2,3,4};
int main()
{
    for(int i=1;i<=n;i++)    q.push(node(a[i],b[i]));
    while(q.size()!=0)
        printf("%d %d\n",q.top().x,q.top().y),q.pop();
    return 0;
}

 

 

 

 

 

注意：priority_queue自定义函数的比较与sort正好是相反的，也就是说，如果你是把大于号作为第一关键字的比较方式，那么堆顶的元素就是第一关键字最小的

 

还可以这么写

 

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int n=5;
struct node
{
    int x,y;
    node(){x=y=0;}
    node(int a,int b){x=a;y=b;}
    bool operator <(const node &a)const 
    {
        if(a.x!=x) return a.x<x;
        return a.y>y;
    }
};
priority_queue<node>q;
int a[15]={0,1,4,4,3,5};
int b[15]={0,2,1,2,3,4};
int main()
{
    for(int i=1;i<=n;i++)    q.push(node(a[i],b[i]));
    while(q.size()!=0)
        printf("%d %d\n",q.top().x,q.top().y),q.pop();
    return 0;
}