素数的筛法
素数的筛法有很多种
在此给出常见的三种方法
以下给出的所有代码均已通过这里的测试
埃拉托斯特尼筛法
名字好长 :joy: 不过代码很短
思路非常简单,对于每一个素数,枚举它的倍数,它的倍数一定不是素数
这样一定可以保证每个素数都会被筛出来
还有,我们第一层循环枚举到$\sqrt(n)$就好,因为如果当前枚举的数大于n,那么它能筛出来的数一定在之前就被枚举过
比如说:
$\sqrt(100)=10$
不难发现我们从$20$枚举所筛去的数一定被$5$筛过
1 #include<cstdio> 2 #include<cmath> 3 using namespace std; 4 const int MAXN=10000001; 5 inline int read() 6 { 7 char c=getchar();int f=1,x=0; 8 while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();} 9 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*f; 10 } 11 int vis[MAXN]; 12 int n,m; 13 int main() 14 { 15 n=read();m=read(); 16 vis[1]=1;//1不是质数 17 for(int i=2;i<=sqrt(n);i++) 18 for(int j=i*i;j<=n;j+=i) 19 vis[j]=1; 20 while(m--) 21 { 22 int p=read(); 23 if(vis[p]==1) printf("No\n"); 24 else printf("Yes\n"); 25 } 26 return 0; 27 }
但是你会发现这份代码只能得30分

看来这种算法还是不够优秀
下面我们来探索一下他的优化
另外,这种算法的时间复杂度:$O(n*logn)$
埃拉托斯特尼筛法优化版
根据唯一分解定理
每一个数都可以被分解成素数乘积的形式
那我们枚举的时候,只有在当前数是素数的情况下,才继续枚举就好
这样可以保证每个素数都会被筛出来
1 #include<cstdio> 2 #include<cmath> 3 using namespace std; 4 const int MAXN=10000001; 5 inline int read() 6 { 7 char c=getchar();int f=1,x=0; 8 while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();} 9 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*f; 10 } 11 int vis[MAXN]; 12 int n,m; 13 int main() 14 { 15 n=read();m=read(); 16 vis[1]=1;//1不是质数 17 for(int i=2;i<=sqrt(n);i++) 18 if(vis[i]==0) 19 for(int j=i*i;j<=n;j+=i) 20 vis[j]=1; 21 while(m--) 22 { 23 int p=read(); 24 if(vis[p]==1) printf("No\n"); 25 else printf("Yes\n"); 26 } 27 return 0; 28 }
果然,加了优化之后这种算法快了不少
可以证明,它的复杂度为:$O(n*log^{logn})$
这种算法已经非常优秀了,但是对于1e7这种极端数据,还是有被卡的风险
那么,还有没有更快的筛法呢?
答案是肯定的!
欧拉筛
我们思考一下第二种筛法的运算过程
不难发现,对于6这个数,它被2筛了一次,又被3筛了一次
第二次筛显然是多余的,
我们考虑去掉这步运算
1 #include<cstdio> 2 #include<cmath> 3 using namespace std; 4 const int MAXN=10000001; 5 inline int read() 6 { 7 char c=getchar();int f=1,x=0; 8 while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();} 9 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*f; 10 } 11 int vis[MAXN],prime[MAXN]; 12 int tot=0; 13 int n,m; 14 int Euler() 15 { 16 vis[1]=1; 17 for(int i=2;i<=n;i++) 18 { 19 if(vis[i]==0) prime[++tot]=i; 20 for(int j=1;j<=tot&&i*prime[j]<=n;j++) 21 { 22 vis[i*prime[j]]=1; 23 if(i%prime[j]==0) break; 24 } 25 } 26 } 27 int main() 28 { 29 n=read();m=read(); 30 Euler(); 31 for(int i=1;i<=m;i++) 32 { 33 int p=read(); 34 if(vis[p]==1) printf("No\n"); 35 else printf("Yes\n"); 36 } 37 return 0; 38 }
对于这份代码,我们分情况讨论
当$i$是素数的时候,那么两个素数的乘积一定没有被筛过,可以避免重复筛
当$i$不是素数的时候
程序中有一句非常关键的话
if(i%prime[j]==0) break;
如果我们把$i$的唯一分解形式表示为$i = p_1^{a_1}p_2^{a_2} \dots p_n^{a_n}$
这句话可以保证:本次循环只能筛除不大于${p_1}*i$的数
这样的话每个数$i$都只能筛除不大于$i$乘$i$的最小素因子的数
反过来,每个数只能被它的最小素因子筛去。
也就可以保证每个数只会被筛一次(这一步好像不是很显然,我在最后会给出证明)
举个例子,
设$i=2*3*5$,此时能筛去$i*2$,但是不能筛去$3*i$
因为如果能晒出$3*i$的话,
当$i_2=3*3*5$时,筛除$2*i_2$就和前面重复了
另外为了方便大家直观理解,给出一张图表
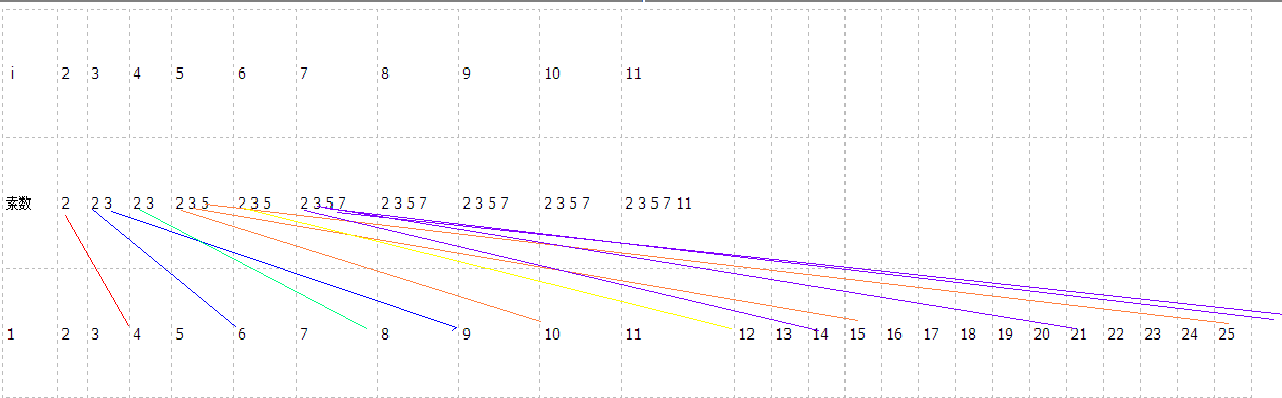
这样显得直观一些
大家好好揣摩揣摩
上面的证明:我自己瞎yy的可能不是很严谨
现在我们需要证明$i = p_1^{a_1}p_2^{a_2} \dots p_n^{a_n}$只会被$p_1$筛去
那么我们需要证明三个条件
1.$i$一定被$p_1$和$p_1^{a_1 - 1}p_2^{a_2} \dots p_n^{a_n}$筛除过
很显然,在枚举到$p_1$之前不会有其他素因子使$p_1^{a_1 - 1}p_2^{a_2} \dots p_n^{a_n}$停止循环
2.$i$不会被$p_1^{a_1}p_2^{a_2 - 1} \dots p_n^{a_n}$筛去
同样也很显然,当枚举到$p_1$时就会停止循环
可以看出这种算法的时间效率是非常高的!
时间复杂度:严格$O(n)$
总结
在一般情况下,第二种筛法已经完全够用。
第三种筛法的优势不仅仅在于速度快,而且还能够筛积性函数,像欧拉函数,莫比乌斯函数等。
这个我以后还会讲的


