Day4下午解题报告
预计分数:30+30+0=60
实际分数:30+30+10=70
稳有个毛线用,,又拿不出成绩来,,
T1
https://www.luogu.org/problem/show?pid=T15626
一开始掉进了数列的坑里就傻乎乎的没出来过
样例给了个3 5 ,推着推着就感觉是斐波那契数列,GG

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<map> 6 #include<ctime> 7 #include<cstdlib> 8 #define LL long long 9 using namespace std; 10 const LL MAXN=1e6; 11 const LL INF=0x7ffff; 12 inline LL read() 13 { 14 char c=getchar();LL flag=1,x=0; 15 while(c<'0'||c>'9') {if(c=='-') flag=-1;c=getchar();} 16 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*flag; 17 } 18 LL f[MAXN]; 19 LL ans=2; 20 map<LL,bool>vis; 21 LL gcd(LL a,LL b) 22 { 23 return b==0?a:gcd(b,a%b); 24 } 25 int main() 26 { 27 // freopen("seq.in","r",stdin); 28 // freopen("seq.out","w",stdout); 29 LL a=read(),b=read(); 30 if(a==b) 31 { 32 printf("2"); 33 return 0; 34 } 35 LL g=gcd(a,b); 36 a/=g,b/=g; 37 f[1]=a,f[2]=b;f[3]=abs(b-a);vis[f[1]]=1;vis[f[2]]=1; 38 LL tot=0; 39 bool flag=0; 40 LL t=clock(); 41 LL x=f[1],y=f[2],z; 42 while(y!=0) 43 { 44 if(clock()-t>=900) 45 { 46 printf("-1"); 47 exit(0); 48 break; 49 } 50 z=abs( x-y ); 51 if(vis[z]==0) 52 ans++,vis[z]=1; 53 x=y,y=z; 54 } 55 printf("%lld",ans); 56 return 0; 57 }
正解:
更相减损术
用除法优化减法
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define LL long long
using namespace std;
inline LL read()
{
char c=getchar();LL flag=1,x=0;
while(c<'0'||c>'9') {if(c=='-') flag=-1;c=getchar();}
while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*flag;
}
LL a,b;
LL ans=0;
int main()
{
a=read();b=read();
if(a<b) swap(a,b);
LL c=a%b;
while(c)
{
ans+=a/b;
a=b;b=c;c=a%b;
}
ans+=a/b;
ans++;
printf("%lld",ans);
return 0;
}
T2
https://www.luogu.org/problem/show?pid=T15627
mdzz裸地暴力一分都没有啊。。。
不过30分的貌似可以套最大生成树做。。
按说用最大生成树可以过50分的,但是我不会判断t。。GG

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<queue> 6 #include<algorithm> 7 using namespace std; 8 const int MAXN=1e5; 9 const int INF=0x7ffff; 10 inline int read() 11 { 12 char c=getchar();int flag=1,x=0; 13 while(c<'0'||c>'9') {if(c=='-') flag=-1;c=getchar();} 14 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*flag; 15 } 16 struct node 17 { 18 int u,v,w,nxt; 19 }edge[MAXN]; 20 int head[MAXN]; 21 int num=1; 22 23 inline void add_edge(int x,int y,int z) 24 { 25 edge[num].u=x; 26 edge[num].v=y; 27 edge[num].w=z; 28 edge[num].nxt=head[x]; 29 head[x]=num++; 30 } 31 int t[MAXN]; 32 int vis[MAXN]; 33 34 35 struct node2 36 { 37 int u2,v2,w2,f2; 38 }edge2[MAXN]; 39 int num2=1; 40 inline void add_edge2(int x2,int y2,int z2) 41 { 42 edge2[num2].u2=x2; 43 edge2[num2].v2=y2; 44 edge2[num2].w2=z2; 45 num2++; 46 } 47 48 49 int bfs(int now,int val) 50 { 51 queue<int>q;q.push(now); 52 int ans=0; 53 memset(vis,0,sizeof(vis));vis[now]=1; 54 while(q.size()!=0) 55 { 56 int p=q.front();q.pop(); 57 for(int i=head[p];i!=-1;i=edge[i].nxt) 58 if(vis[edge[i].v]==0&&edge[i].w>=val) 59 vis[edge[i].v]=1,q.push(edge[i].v),ans++; 60 } 61 return ans; 62 } 63 int fa[MAXN]; 64 int n,m; 65 int comp(const node2 &a,const node2 &b) 66 { 67 return a.w2>b.w2; 68 } 69 int find(int x) 70 { 71 if(fa[x]==x) return x; 72 else return fa[x]=find(fa[x]); 73 } 74 inline void unionn(int x,int y) 75 { 76 fa[find(x)]=find(y); 77 } 78 void kruskal() 79 { 80 sort(edge2+1,edge2+num2,comp); 81 int tot=0; 82 for(int i=1;i<=num2-1;i++) 83 { 84 if(find(edge2[i].u2)!=find(edge2[i].v2)) 85 { 86 unionn(edge2[i].u2,edge2[i].v2); 87 add_edge(edge2[i].u2,edge2[i].v2,edge2[i].w2); 88 add_edge(edge2[i].v2,edge2[i].u2,edge2[i].w2); 89 tot++; 90 if(tot==n-1) break; 91 } 92 } 93 } 94 int main() 95 { 96 //freopen("car.in","r",stdin); 97 // freopen("car.out","w",stdout); 98 memset(head,-1,sizeof(head)); 99 n=read(),m=read(); 100 for(int i=1;i<=n;i++) 101 fa[i]=i; 102 if(n<=0) 103 { 104 for(int i=1;i<=m;i++) 105 { 106 int x=read(),y=read(),z=read(); 107 add_edge(x,y,z); 108 add_edge(y,x,z); 109 } 110 for(int i=1;i<=n;i++)// 枚举所有点 111 { 112 int now=1,out=0; 113 while(1) 114 { 115 int p=bfs(i,now); 116 if(p==0) break; 117 t[now++]=p; 118 } 119 for(int i=1;i<=now-1;i++) 120 out+=abs(t[i]-t[i+1])*abs(t[i]-t[i+1]); 121 printf("%d ",out); 122 } 123 } 124 else 125 { 126 for(int i=1;i<=m;i++) 127 { 128 int x=read(),y=read(),z=read(); 129 add_edge2(x,y,z); 130 add_edge2(y,x,z); 131 } 132 kruskal(); 133 for(int i=1;i<=n;i++)// 枚举所有点 134 { 135 memset(t,0,sizeof(t)); 136 int now=1,out=0; 137 while(1) 138 { 139 int p=bfs(i,now); 140 if(p==0) break; 141 t[now++]=p; 142 } 143 for(int i=1;i<=now-1;i++) 144 out+=abs(t[i]-t[i+1])*abs(t[i]-t[i+1]); 145 printf("%d ",out); 146 } 147 } 148 return 0; 149 } 150 151 /* 152 153 3 2 154 1 2 1 155 2 3 2 156 157 4 5 158 1 4 2 159 1 2 3 160 2 4 1 161 2 3 4 162 3 4 2 163 164 */
正解
最大生成树
用并查集维护的时候,每次维护的时候在两个点上面新开一个节点
这样就形成了一颗二叉树
剩下的就不会了。。。
https://www.luogu.org/problem/show?pid=T15628
T3
https://www.luogu.org/problem/show?pid=T15628
一眼动态规划,
很好写,但是时间复杂度是O(n*m*k)GG,一分没有

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 using namespace std; 6 const int MAXN=5001; 7 const int INF=0x7ffff; 8 inline int read() 9 { 10 char c=getchar();int flag=1,x=0; 11 while(c<'0'||c>'9') {if(c=='-') flag=-1;c=getchar();} 12 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*flag; 13 } 14 int dp[MAXN][MAXN]; 15 // 第i个数 已经选了j个 第i个一定选 最小值 16 int a[MAXN]; 17 int main() 18 { 19 // freopen("number.in","r",stdin); 20 // freopen("number.out","w",stdout); 21 int n=read(),m=read(),need=read(); 22 memset(dp,0x3f,sizeof(dp)); 23 for(int i=1;i<=n;i++) a[i]=dp[i][1]=read(); 24 for(int i=1;i<=n;i++) 25 for(int j=i-m;j>=1;j--) 26 for(int k=2;k<=need;k++) 27 dp[i][k]=min(dp[i][k],dp[j][k-1]+a[i]); 28 int ans=INF; 29 for(int i=1;i<=n;i++) 30 ans=min(ans,dp[i][need]); 31 printf("%d",ans); 32 return 0; 33 } 34 /* 35 6 2 3 36 9 8 1 3 5 4 //14 37 38 5 2 2 39 4 7 1 1 1//2 40 41 5 2 2 42 4 3 44 44 1 //4 43 44 7 3 1 45 4 6 7 1 2 3 4// 1 46 47 7 3 3 48 4 6 7 1 2 3 4// 9 49 50 */
正解
我就不吐槽啥了
这**出题人压根就没给暴力分啊。
考虑如何在O(n)内算出不考虑k,只考虑m的最大值
很显然的一个结论
设f(x)为1-n中,长度为m的限制下,选x个数的图像的增长区线
那么f(x)会增长的越来越快
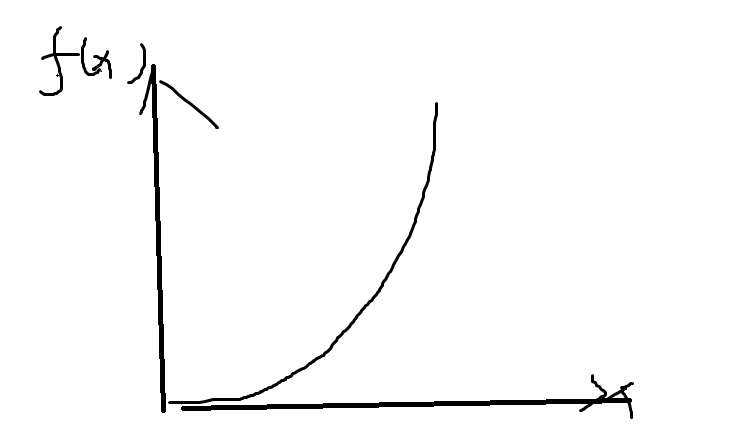
二分一个c,为(k-1,f(k-1) ) 与 (k,f(k) ) 的斜率

1 #include<cstdio> 2 #include<cstdlib> 3 #include<iostream> 4 #include<algorithm> 5 #include<cstring> 6 using namespace std; 7 typedef long long LL; 8 const int N=1000010; 9 const LL inf=10000000; 10 int n,m,x,y,z,L,sum; 11 int cnt[N]; 12 LL ans0,ans; 13 LL f[N],s[N]; 14 LL read() 15 { 16 LL x=0,f=1;char ch=getchar(); 17 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 18 while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} 19 return x*f; 20 } 21 void solve(LL c) 22 { 23 int i,a,tot=0; 24 LL ss=0; 25 memset(cnt,0,sizeof(cnt)); 26 memset(f,0,sizeof(f)); 27 for(i=1;i<=n;i++) 28 { 29 a=i-m; 30 if(a>=1&&c-s[a]>0&&(f[a]>ss||(f[a]==ss&&cnt[a]<tot))) 31 { 32 ss=f[a]; 33 tot=cnt[a]; 34 } 35 if(c-s[i]>0) 36 { 37 f[i]=ss+c-s[i]; 38 cnt[i]=tot+1; 39 } 40 } 41 ans0=sum=0; 42 for(i=1;i<=n;i++) 43 if(f[i]>ans0||(f[i]==ans0&&sum>cnt[i])) 44 { 45 sum=cnt[i]; 46 ans0=f[i]; 47 } 48 // printf("%d %lld %lld\n",sum,c,ans0); 49 } 50 int pd(LL c) 51 { 52 solve(c); 53 if(sum<L) return 1; 54 else return 0; 55 } 56 int main() 57 { 58 int a,b,c,i,j,k; 59 LL l,r; 60 freopen("number.in","r",stdin); 61 freopen("number.out","w",stdout); 62 n=read(); 63 m=read(); 64 L=read(); 65 for(i=1;i<=n;i++) 66 s[i]=read(); 67 // for(i=1;i<=n;i++) 68 // if(i%m==1) ans+=(LL)s[i]; 69 // printf("%lld\n",ans); 70 ans=0; 71 l=0; 72 r=(LL)inf*N/2; 73 while(l<r-1) 74 { 75 LL mid=(l+r)/2; 76 if(pd(mid)) l=mid; 77 else r=mid; 78 } 79 if(pd(r)) 80 { 81 solve(r); 82 ans=(LL)L*r-ans0; 83 // printf("%d\n",sum); 84 } 85 else 86 { 87 solve(l); 88 ans=(LL)L*l-ans0; 89 } 90 printf("%lld\n",ans); 91 } 92 /* 93 6 5 2 94 100 1 1 1 1 100 95 */
总结
上午那场,出题人给了:50+80+0的暴力,我正好没做T2
下午这场,出题人给了:30+30+0的暴力,我正好做了T3
mmp..
摆明了把我这种纯暴力选手往死里坑啊,,,,
不过还好明天就不是这个出题人了,(*  ̄︿ ̄)(*  ̄︿ ̄)(*  ̄︿ ̄)(*  ̄︿ ̄)(*  ̄︿ ̄)(*  ̄︿ ̄)(*  ̄︿ ̄)(*  ̄︿ ̄)
作者:自为风月马前卒
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。



