模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板
网络流
匈牙利

#include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #include<vector> #define LL long long using namespace std; const int MAXN = 1e3 + 10, INF = 1e9 + 10; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } vector<int> v[MAXN]; int N, M, E; int link[MAXN], vis[MAXN], cur = 1; int Aug(int x) { for(int i = 0; i < v[x].size(); i++) { int to = v[x][i]; if(vis[to] == cur) continue; vis[to] = cur; if(!link[to] || Aug(link[to])) { link[to] = x; return 1; } } return 0; } main() { #ifdef WIN32 freopen("a.in", "r", stdin); //freopen("b.out", "w", stdout); #endif int N = read(), M = read(), E = read(); for(int i = 1; i <= E; i++) { int x = read(), y = read(); if(x <= N && y <= M) { v[x].push_back(y); //v[y].push_back(x); } } int ans = 0; for(int i = 1; i <= N; i++, cur++) if(Aug(i)) ans++; printf("%d\n", ans); return 0; }
Dinic

// luogu-judger-enable-o2 #include<cstring> #include<cstdio> #define add_edge(x, y, z) AddEdge(x, y, z); AddEdge(y, x, 0); #define min(x, y) x < y ? x : y #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 19, stdin), p1 == p2) ? EOF : *p1++) #define rg register const int MAXN = 10001, INF = 1e9 + 10; char buf[1 << 19], *p1 = buf, *p2 = buf; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9'){if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int N, M, S, T; struct node { int u, v, f, nxt; }E[200002]; int head[MAXN], cur[MAXN], num = 0, deep[MAXN], vis[MAXN], q[MAXN]; inline void AddEdge(int x, int y, int z) { E[num] = (node){x, y, z, head[x]}; head[x] = num++; } inline bool BFS() { int l = 1, r = 1; q[r++] = S; memset(deep, 0, sizeof(deep)); deep[S] = 1; while(l < r) { int p = q[l++]; for(rg int i = head[p]; i != -1; i = E[i].nxt) { if(E[i].f && !deep[E[i].v]) { deep[E[i].v] = deep[p] + 1; if(E[i].v == T) return deep[T]; q[r++] = E[i].v; } } } return deep[T]; } int DFS(int x, int flow) { if(x == T) return flow; int ansflow = 0; for(rg int &i = cur[x]; i != -1; i = E[i].nxt) { if(deep[E[i].v] == deep[x] + 1 && E[i].f) { int canflow = DFS(E[i].v, min(E[i].f, flow)); flow -= canflow; E[i].f -= canflow; E[i ^ 1].f += canflow; ansflow += canflow; if(flow <= 0) break; } } return ansflow; } inline int Dinic() { int ans = 0; while(BFS()) { memcpy(cur, head, sizeof(head)); ans += DFS(S, INF); } return ans; } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); #endif memset(head, -1, sizeof(head)); N = read(); M = read(); S = read(); T = read(); for(rg int i = 1; i <= M; i++) { rg int x = read(), y = read(), z = read(); add_edge(x, y, z); } printf("%d", Dinic()); return 0; }
最小费用最大流

// luogu-judger-enable-o2 /* */ #include<cstdio> #include<algorithm> #include<cstring> #include<queue> using namespace std; const int MAXN = 1e5 + 10, INF = 1e9 + 10; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = 1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int N, M, S, T; struct Edge { int u, v, w, f, nxt; }E[MAXN]; int head[MAXN], num = 0; inline void AddEdge(int x, int y, int w, int f) { E[num] = (Edge){x, y, w, f, head[x]}; head[x] = num++; } int anscost, ansflow, dis[MAXN], vis[MAXN], Pre[MAXN]; bool SPFA() { memset(dis, 0x3f, sizeof(dis)); memset(vis, 0, sizeof(vis)); queue<int> q; q.push(S); dis[S] = 0; while(!q.empty()) { int p = q.front(); q.pop(); vis[p] = 0; for(int i = head[p]; i !=- 1; i = E[i].nxt) { int to = E[i].v; if(dis[to] > dis[p] + E[i].w && E[i].f) { dis[to] = dis[p] + E[i].w; Pre[to] = i; if(!vis[to]) q.push(to), vis[to] = 1; } } } return dis[T] <= INF; } int F() { int nowflow = INF; for(int i = T; i != S; i = E[Pre[i]].u) nowflow = min(nowflow, E[Pre[i]].f); for(int i = T; i != S; i = E[Pre[i]].u) E[Pre[i]].f -= nowflow, E[Pre[i] ^ 1].f += nowflow; anscost += dis[T] * nowflow; ansflow += nowflow; } void MCMF() { while(SPFA()) F(); } int main() { memset(head, -1, sizeof(head)); N = read(); M = read(); S = read(); T = read(); for(int i = 1; i <= M; i++) { int x = read(), y = read(), f = read(), w = read(); AddEdge(x, y, w, f); AddEdge(y, x, -w, 0); } MCMF(); printf("%d %d", ansflow, anscost); return 0; } /* */
图论
最短路
SPFA

1 #include<cstdio> 2 #include<queue> 3 #include<cstring> 4 using namespace std; 5 const int MAXN=1000001; 6 inline void read(int &n) 7 { 8 char c=getchar();bool flag=0;n=0; 9 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 10 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 11 } 12 13 struct node 14 { 15 int u,v,w,nxt; 16 }edge[MAXN]; 17 int head[MAXN]; 18 int num=1; 19 inline void add_edge(int x,int y,int z) 20 { 21 edge[num].u=x; edge[num].v=y; 22 edge[num].w=z; edge[num].nxt=head[x]; 23 head[x]=num++; 24 } 25 int N,M,S=1;; 26 int dis[MAXN],vis[MAXN]; 27 inline void SPFA() 28 { 29 queue<int>q;q.push(S); 30 while(q.size()!=0) 31 { 32 int p=q.front(); 33 q.pop();vis[p]=0; 34 for(int i=head[p];i!=-1;i=edge[i].nxt) 35 if(dis[edge[i].v]>dis[edge[i].u]+edge[i].w) 36 { 37 dis[edge[i].v]=dis[edge[i].u]+edge[i].w; 38 if(!vis[edge[i].v]) vis[edge[i].v]=1,q.push(edge[i].v); 39 } 40 } 41 } 42 int main()/*S到其他节点的最短路*/ 43 { 44 memset(head,-1,sizeof(head)); 45 read(N);read(M);read(S); 46 for(int i=1;i<=N;i++) dis[i]=2147483647; dis[S]=0; 47 for(int i=1;i<=M;i++) 48 { 49 int x,y,z;read(x);read(y);read(z); 50 add_edge(x,y,z); 51 } 52 SPFA(); 53 for(int i=1;i<=N;i++) printf("%d ",dis[i]); 54 return 0; 55 }

1 #include<cstdio> 2 #include<deque> 3 #include<cstring> 4 using namespace std; 5 const int MAXN=1000001; 6 inline void read(int &n) 7 { 8 char c=getchar();bool flag=0;n=0; 9 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 10 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 11 } 12 13 struct node 14 { 15 int u,v,w,nxt; 16 }edge[MAXN]; 17 int head[MAXN]; 18 int num=1; 19 inline void add_edge(int x,int y,int z) 20 { 21 edge[num].u=x; edge[num].v=y; 22 edge[num].w=z; edge[num].nxt=head[x]; 23 head[x]=num++; 24 } 25 int N,M,S=1;; 26 int dis[MAXN],vis[MAXN]; 27 inline void SPFA() 28 { 29 deque<int>q;q.push_front(S); 30 while(q.size()!=0) 31 { 32 int p=q.front(); 33 q.pop_front();vis[p]=0; 34 for(int i=head[p];i!=-1;i=edge[i].nxt) 35 if(dis[edge[i].v]>dis[edge[i].u]+edge[i].w) 36 { 37 dis[edge[i].v]=dis[edge[i].u]+edge[i].w; 38 if(!vis[edge[i].v]) vis[edge[i].v]=1,q.size()!=0&&dis[edge[i].v]<dis[q.front()]?q.push_front(edge[i].v):q.push_back(edge[i].v); 39 } 40 } 41 } 42 int main()/*S到其他节点的最短路*/ 43 { 44 memset(head,-1,sizeof(head)); 45 read(N);read(M);read(S); 46 for(int i=1;i<=N;i++) dis[i]=2147483647; dis[S]=0; 47 for(int i=1;i<=M;i++) 48 { 49 int x,y,z;read(x);read(y);read(z); 50 add_edge(x,y,z); 51 } 52 SPFA(); 53 for(int i=1;i<=N;i++) printf("%d ",dis[i]); 54 return 0; 55 }

1 #include<cstdio> 2 #include<cstring> 3 #include<ext/pb_ds/priority_queue.hpp> 4 using namespace __gnu_pbds; 5 const int MAXN=1000001; 6 inline void read(int &n) 7 { 8 char c=getchar();bool flag=0;n=0; 9 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 10 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 11 } 12 13 struct node 14 { 15 int u,v,w,nxt; 16 }edge[MAXN]; 17 int head[MAXN]; 18 int num=1; 19 inline void add_edge(int x,int y,int z) 20 { 21 edge[num].u=x; edge[num].v=y; 22 edge[num].w=z; edge[num].nxt=head[x]; 23 head[x]=num++; 24 } 25 int N,M,S=1;; 26 int dis[MAXN],vis[MAXN]; 27 struct Compare 28 { 29 __inline__ __attribute((always_inline)) bool operator()(int a,int b)//我以前的题解提到过的强制inline的方法 30 { 31 return dis[a]>dis[b]; 32 } 33 };//自定义比较器 34 inline void SPFA() 35 { 36 priority_queue<int,Compare>q; 37 q.push(S); 38 while(q.size()!=0) 39 { 40 int p=q.top(); 41 q.pop();vis[p]=0; 42 for(int i=head[p];i!=-1;i=edge[i].nxt) 43 if(dis[edge[i].v]>dis[edge[i].u]+edge[i].w) 44 { 45 dis[edge[i].v]=dis[edge[i].u]+edge[i].w; 46 if(!vis[edge[i].v]) vis[edge[i].v]=1,q.push(edge[i].v); 47 } 48 } 49 } 50 int main()/*S到其他节点的最短路*/ 51 { 52 memset(head,-1,sizeof(head)); 53 read(N);read(M);read(S); 54 for(int i=1;i<=N;i++) dis[i]=2147483647; dis[S]=0; 55 for(int i=1;i<=M;i++) 56 { 57 int x,y,z;read(x);read(y);read(z); 58 add_edge(x,y,z); 59 } 60 SPFA(); 61 for(int i=1;i<=N;i++) printf("%d ",dis[i]); 62 return 0; 63 }
Floyd

1 #include<cstdio> 2 #include<queue> 3 #include<cstring> 4 using namespace std; 5 const int MAXN=2501; 6 inline void read(int &n) 7 { 8 char c=getchar();bool flag=0;n=0; 9 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 10 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 11 } 12 long long int map[MAXN][MAXN]; 13 int main()/*S到T的最短路*/ 14 { 15 int N,M,S,T; 16 read(N);read(M);read(S);read(T); 17 for(int i=1;i<=N;i++) for(int j=1;j<=N;j++) map[i][j]=0x7fffff; 18 for(int i=1;i<=M;i++) 19 { 20 int x,y,z;read(x);read(y);read(z); 21 map[x][y]=z;map[y][x]=z; 22 } 23 for(int k=1;k<=N;k++) 24 for(int i=1;i<=N;i++) 25 for(int j=1;j<=N;j++) 26 map[i][j]=min(map[i][j],map[i][k]+map[k][j]); 27 printf("%lld ",map[S][T]); 28 return 0; 29 }

1 #include<cstdio> 2 #include<queue> 3 #include<cstring> 4 using namespace std; 5 const int MAXN=2501; 6 inline void read(int &n) 7 { 8 char c=getchar();bool flag=0;n=0; 9 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 10 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 11 } 12 long long int map[MAXN][MAXN]; 13 int main()/*S到T的最短路*/ 14 { 15 int N,M,S,T; 16 read(N);read(M);read(S);read(T); 17 for(int i=1;i<=N;i++) for(int j=1;j<=N;j++) map[i][j]=0x7fffff; 18 for(int i=1;i<=M;i++) 19 { 20 int x,y,z;read(x);read(y);read(z); 21 map[x][y]=z;map[y][x]=z; 22 } 23 for(int k=1;k<=N;k++) 24 for(int i=1;i<=N;i++) 25 for(int j=1;j<=i;j++) 26 map[j][i]=map[i][j]=min(map[i][j],map[i][k]+map[k][j]); 27 printf("%lld ",map[S][T]); 28 return 0; 29 }
堆优化dijkstra

// luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<cstdio> #include<algorithm> #include<cstring> #include<ext/pb_ds/priority_queue.hpp> #define MP(x, y) make_pair(x, y) #define Pair pair<int, int> using namespace std; const int MAXN = 1e6 + 10, INF = 2147483646, B = 19; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = 1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int N, M, S; struct Edge { int u, v, w, nxt; }E[MAXN]; int head[MAXN], num = 1; void AddEdge(int x, int y, int z) { E[num] = (Edge) {x, y, z, head[x]}; head[x] = num++; } int dis[MAXN], vis[MAXN]; priority_queue<Pair> q; void Dij() { for(int i = 1; i <= N; i++) dis[i] = 2147483647; dis[S] = 0; q.push(MP(0, S)); while(!q.empty()) { int p = q.top().second; q.pop(); if(vis[p]) continue; vis[p] = 1; for(int i = head[p]; i != -1; i = E[i].nxt) { int to = E[i].v; if(dis[to] > dis[p] + E[i].w) dis[to] = dis[p] + E[i].w, q.push(MP(-dis[to], to)); } } for(int i = 1; i <= N; i++) printf("%d ", dis[i]); } main() { memset(head, -1, sizeof(head)); N = read(); M = read(); S = read(); for(int i = 1; i <= M; i++) { int x = read(), y = read(), z = read(); AddEdge(x, y, z); } Dij(); return 0; }
最小生成树
Kruskal

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 using namespace std; 7 const int MAXN=400002; 8 inline void read(int &n) 9 { 10 char c=getchar();bool flag=0;n=0; 11 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 12 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 13 } 14 struct node 15 { 16 int u,v,w; 17 }edge[MAXN]; 18 int num=1; 19 inline void add_edge(int x,int y,int z) 20 { 21 edge[num].u=x; 22 edge[num].v=y; 23 edge[num].w=z; 24 num++; 25 } 26 int comp(const node &a,const node &b) 27 { 28 return a.w<b.w; 29 } 30 int fa[MAXN]; 31 int n,m; 32 int find(int x) 33 { 34 if(fa[x]==x) return fa[x]; 35 else return fa[x]=find(fa[x]); 36 } 37 int unionn(int x,int y) 38 { 39 fa[find(x)]=find(y); 40 } 41 inline void Kruskal() 42 { 43 int ans=0,tot=0; 44 sort(edge+1,edge+num,comp); 45 for(int i=1;i<=num-1;i++) 46 { 47 if(find(edge[i].u)!=find(edge[i].v)) 48 { 49 unionn(edge[i].u,edge[i].v); 50 tot++; 51 ans+=edge[i].w; 52 if(tot==n-1) 53 { 54 printf("%d",ans); 55 exit(0); 56 } 57 } 58 } 59 printf("orz"); 60 } 61 int main() 62 { 63 read(n);read(m); 64 for(int i=1;i<=n;i++) fa[i]=i; 65 for(int i=1;i<=m;i++) 66 { 67 int x,y,z; 68 read(x);read(y);read(z); 69 add_edge(x,y,z); 70 } 71 Kruskal(); 72 return 0; 73 }
tarjan

// luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<stack> #include<vector> #include<queue> #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) char buf[1<<21],*p1=buf,*p2=buf; using namespace std; const int MAXN=1000001; const int INF=1e9+7; inline int read() { char c=getchar();register int x=0; while(c<'0'||c>'9')c=getchar(); while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar(); return x; } char obuf[1<<24],*O=obuf; inline void print(int x) { if(x>9) print(x/10); *O++=x%10+'0'; } int val[MAXN]; struct node { int u,v,nxt; }edge[MAXN]; int head[MAXN],num=1; inline void AddEdge(int x,int y) { edge[num].u=x; edge[num].v=y; edge[num].nxt=head[x]; head[x]=num++; } vector<int>E[MAXN]; int color[MAXN],colornum=0,low[MAXN],dfn[MAXN],vis[MAXN],sum[MAXN],tot=0; stack<int>s; void tarjan(int now) { dfn[now]=low[now]=++tot; s.push(now);vis[now]=1; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(!dfn[edge[i].v]) tarjan(edge[i].v),low[now]=min(low[now],dfn[edge[i].v]); if(vis[edge[i].v]) low[now]=min(low[now],low[edge[i].v]); } if(low[now]==dfn[now]) { int h;colornum++; do { h=s.top(); color[h]=colornum; sum[colornum]+=val[h]; vis[h]=0; s.pop(); }while(now!=h); } } int inder[MAXN],dp[MAXN],ans=0; void Topsort() { queue<int>q; for(int i=1;i<=colornum;i++) dp[i]=sum[i]; for(int i=1;i<=colornum;i++) if(inder[i]==0) q.push(i); while(q.size()!=0) { int p=q.front();q.pop(); for(int i=0;i<E[p].size();i++) { inder[E[p][i]]--; dp[E[p][i]]=max(dp[E[p][i]],dp[p]+sum[E[p][i]]); if(inder[E[p][i]]==0) q.push(E[p][i]); } } for(int i=1;i<=colornum;i++) ans=max(ans,dp[i]); printf("%d",ans); } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #endif memset(head,-1,sizeof(head)); int N=read(),M=read(); for(int i=1;i<=N;i++) val[i]=read(); for(int i=1;i<=M;i++) { int x=read(),y=read(); AddEdge(x,y); } for(int i=1;i<=N;i++) if(!color[i]) tarjan(i); for(int i=1;i<=N;i++) for(int j=head[i];j!=-1;j=edge[j].nxt) if(color[i]!=color[edge[j].v]) E[color[i]].push_back(color[edge[j].v]), inder[color[edge[j].v]]++; Topsort(); return 0; }

void tarjan(int now) { dfn[now]=low[now]=++tot; s.push(now); vis[now]=1; for(int i=headE[now];i!=-1;i=E[i].nxt) { if(!dfn[E[i].v]) tarjan(E[i].v),low[now]=min(low[now],low[E[i].v]); else if(vis[E[i].v]) low[now]=min(low[now],dfn[E[i].v]); } if(low[now]==dfn[now]) { int h; colornum++; do { h=s.top(); color[h]=colornum; sum[colornum]+=money[h]; vis[h]=0; s.pop(); }while(h!=now); } }

void tarjan(int now,int fa) { dfn[now]=low[now]=++tot; s.push(now); for(int i=head[now];i!=-1;i=edge[i].nxt) { if(!dfn[edge[i].v]&&edge[i].v!=fa) { tarjan(edge[i].v,now); low[now]=min(low[now],low[edge[i].v]); if(low[edge[i].v]>=dfn[now]) { memset(in,0,sizeof(in));//哪些在双联通分量里 memset(color,0,sizeof(color)); int h=0,cnt=0; do { h=s.top();s.pop(); in[h]=1; point[++cnt]=h; }while(h!=edge[i].v);//warning if(cnt<=1) continue;//必须构成环 in[now]=1;point[++cnt]=now; if(MakeColor(now,1)==0) for(int j=1;j<=cnt;j++) ans[point[j]]=1; } } if(edge[i].v!=fa) low[now]=min(low[now],dfn[edge[i].v]); } }

void tarjan(int now,int fa) { dfn[now]=low[now]=++tot; s.push(now); vis[now]=1; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(!dfn[edge[i].v]&&edge[i].v!=fa) tarjan(edge[i].v,now),low[now]=min(low[now],low[edge[i].v]); if(vis[edge[i].v]&&edge[i].v!=fa) low[now]=min(low[now],dfn[edge[i].v]); } if(dfn[now]==low[now]) { int h=0; colornum++; do { h=s.top(); color[h]=colornum; s.pop(); }while(h!=now); } }

int tarjan(int now,int fa) { int ch=0; dfn[now]=low[now]=++tot; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(!dfn[edge[i].v]) { tarjan(edge[i].v,fa); low[now]=min(low[now],low[edge[i].v]); if(low[edge[i].v]>=dfn[now]&&now!=fa) cut[now]=1; if(now==fa) ch++; } low[now]=min(low[now],dfn[edge[i].v]); } if(now==fa&&ch>=2) cut[now]=1; }

void tarjan(int now,int fa) { dfn[now]=low[now]=++tot; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(!dfn[edge[i].v]) { deep[edge[i].v]=deep[now]+1; f[edge[i].v]=now; tarjan(edge[i].v,now); low[now]=min(low[now],low[edge[i].v]); if(low[edge[i].v]>dfn[now]) { bridge[edge[i].v]=1; ans++; } } else if(edge[i].v!=fa) low[now]=min(low[now],dfn[edge[i].v]); } }
数论
BSGS

int BSGS(int a, int b, int p) {//a^x = b % p int M = ceil(sqrt(p)), base = fp(a, M), g = __gcd(a, p); if(g != 1) return -1; static map<int, int> mp; mp.clear(); for(int i = 0, now = b; i <= M; i++, now = mul(now, a)) mp[now] = i + 1; for(int i = 1, now = base; i <= M; i++, now = mul(now, base)) if(mp[now]) return i * M - mp[now] + 1; return -1; }
扩展欧几里得
https://www.luogu.org/problem/show?pid=1082

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<queue> 7 using namespace std; 8 const int MAXN=100001; 9 inline void read(int &n) 10 { 11 char c=getchar();bool flag=0;n=0; 12 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 13 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 14 } 15 int a[6],b[6]; 16 int exgcd(int a,int b,int &x,int &y) 17 { 18 if(b==0) 19 { x=1,y=0;return a; } 20 int r=exgcd(b,a%b,x,y); 21 int tmp=x;x=y;y=tmp-(a/b)*y; 22 return r; 23 } 24 int x,y; 25 int main() 26 { 27 int a,b; 28 read(a);read(b); 29 int r=exgcd(a,b,x,y); 30 while(x<0) x+=b; 31 printf("%d",x); 32 return 0; 33 }

int x, y; int exgcd(int a, int b, int &x, int &y) { if(b == 0) {x = 1, y = 0; return a;} int r = exgcd(b, a % b, x, y), tmp; tmp = x; x = y; y = tmp - a / b * y; return r; } int solve(int a, int b, int mod) {//ax + mody = b int g = exgcd(a, mod, x, y); if(b % g) return -1; x = mul(x, (b / g)); mod = mod / g; while(x < 0) x += mod; return x % mod; }
CRT

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<queue> 7 #define LL long long 8 using namespace std; 9 const LL MAXN=100001; 10 const LL n=4; 11 inline void read(LL &n) 12 { 13 char c=getchar();bool flag=0;n=0; 14 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 15 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 16 } 17 LL a[MAXN],b[MAXN]; 18 LL exgcd(LL a,LL b,LL &x,LL &y) 19 { 20 if(b==0) 21 { x=1,y=0;return a; } 22 LL r=exgcd(b,a%b,x,y); 23 LL tmp=x;x=y;y=tmp-(a/b)*y; 24 return r; 25 } 26 LL x,y; 27 LL gcd(LL a,LL b) 28 { 29 return b==0?a:gcd(b,a%b); 30 } 31 LL CRT() 32 { 33 LL M=1,ans=0; 34 for(LL i=1;i<=n;i++) M*=a[i]; 35 for(LL i=1;i<=n;i++) 36 { 37 LL r=exgcd(M/a[i],a[i],x,y); 38 ans=( ans+b[i]*(M/a[i])*x )%M; 39 } 40 while(ans<0) ans+=M; 41 return ans; 42 } 43 int main() 44 { 45 46 for(LL i=1;i<=n;i++) 47 read(a[i]),read(b[i]); 48 printf("%lld",CRT()); 49 return 0; 50 }
扩展CRT

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<queue> 7 using namespace std; 8 const int MAXN=100001; 9 const int n=4; 10 inline void read(int &n) 11 { 12 char c=getchar();bool flag=0;n=0; 13 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 14 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 15 } 16 int a[MAXN],b[MAXN]; 17 int exgcd(int a,int b,int &x,int &y) 18 { 19 if(b==0) 20 { x=1,y=0;return a; } 21 int r=exgcd(b,a%b,x,y); 22 int tmp=x;x=y;y=tmp-(a/b)*y; 23 return r; 24 } 25 int x,y; 26 int gcd(int a,int b) 27 { 28 return b==0?a:gcd(b,a%b); 29 } 30 inline int EX_CRT() 31 { 32 /* 33 x+a1*y1=b1 1 34 x+a2*y2=b2 2 35 x+a3*y3=b3 3 36 求这个方程的解x 37 */ 38 int M=a[1],R=b[1],x,y; 39 // M=LCM(a1,a2) 40 // R=bi-b1 41 for(int i=2;i<=n;i++) 42 { 43 44 /* 45 a1*y1-a2*y2=b2-b1 46 a*x +b*y =gcd(a,b) 47 这样求出y1之后 48 带回得到对于1,2两个方程的解x0=b1-y1*a1 49 */ 50 int r=exgcd(M,a[i],x,y); 51 if( (R-b[i])%r!=0) return -1; 52 /* R-b[i]相当于b2-b1 53 方程有解的条件(b2-b1)%gcd(a,b) ==0 */ 54 55 x=(R-b[i])/r*x%a[i];//**** 56 57 58 R=R-x*M;//x0=b1-y1*a1 59 M=M/r*a[i];// 新的模数 60 R=R%M;//R=X mod M 61 } 62 return (R%M+M)%M; 63 } 64 int main() 65 { 66 67 for(int i=1;i<=n;i++) 68 read(a[i]),read(b[i]); 69 printf("%d",EX_CRT()); 70 return 0; 71 }
快速幂

1 #include<cstdio> 2 #include<deque> 3 #include<cstring> 4 #define LL long long 5 using namespace std; 6 const LL MAXN=1000001; 7 inline void read(LL &n) 8 { 9 char c=getchar();bool flag=0;n=0; 10 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 11 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 12 } 13 LL a,p,mod,base; 14 LL fastpow(LL a,LL p) 15 { 16 for(base=1;p;p>>=1) p&1?base=(base*a)%mod,a=(a*a)%mod:a=(a*a)%mod; 17 return base; 18 } 19 int main() 20 { 21 22 read(a);read(p);read(mod); 23 printf("%lld^%lld mod %lld=%lld",a,p,mod,fastpow(a,p)); 24 return 0; 25 }
卡特兰数
https://www.luogu.org/problem/show?pid=1976

1 #include<cstdio> 2 const int MAXN=100001; 3 inline int read() 4 { 5 char c=getchar();int x=0,flag=1; 6 while(c<'0'||c>'9') {if(c=='-') flag=-1;c=getchar();} 7 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*flag; 8 } 9 int n; 10 long long dp[MAXN]; 11 int main() 12 { 13 n=read(); 14 dp[0]=1; 15 int ans=0; 16 for(int i=1;i<=n;i++) 17 for(int j=0;j<i;j++) 18 dp[i]=(dp[i]+(dp[j]*dp[i-j-1])%100000007)%100000007; 19 printf("%lld",dp[n]%100000007); 20 return 0; 21 }
字符串
KMP

#include<cstdio> #include<cstring> using namespace std; const int MAXN = 1e6 + 10; char s1[MAXN], s2[MAXN]; int N1, N2; int fail[MAXN]; void GetFail() { int now = 0; for(int i = 2; i <= N2; i++) { while(now && s2[i] != s2[now + 1]) now = fail[now]; if(s2[i] == s2[now + 1]) now++; fail[i] = now; } } void KMP() { int now = 0; for(int i = 1; i <= N1; i++) { while(now && s1[i] != s2[now + 1]) now = fail[now]; if(s1[i] == s2[now + 1]) now++; if(now == N2) printf("%d\n", i - N2 + 1), now= fail[now]; } } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); //freopen("a.out", "w", stdout); #endif scanf("%s %s", s1 + 1, s2 + 1); N1 = strlen(s1 + 1); N2 = strlen(s2 + 1); GetFail(); KMP(); for(int i = 1; i <= N2; i++) printf("%d ", fail[i]); return 0; }
后缀数组
http://www.cnblogs.com/zwfymqz/p/8430014.html

#include<cstdio> #include<iostream> #include<cstring> using namespace std; const int MAXN=2*1e6+10; int sa[MAXN],rak[MAXN],tp[MAXN],tax[MAXN],a[MAXN],N,M,height[MAXN]; char s[MAXN]; void Qsort() { for(int i=1;i<=M;i++) tax[i]=0; for(int i=1;i<=N;i++) tax[rak[i]]++; for(int i=1;i<=M;i++) tax[i]+=tax[i-1]; for(int i=N;i>=1;i--) sa[ tax[rak[tp[i]]]-- ] = tp[i]; } void Ssort() { M=127; for(int i=1;i<=N;i++) rak[i]=a[i],tp[i]=i;Qsort(); for(int w=1,p=1; p<N ; w<<=1,M=p) { p=0; for(int i=N-w+1;i<=N;i++) tp[++p]=i; for(int i=1;i<=N;i++) if(sa[i]>w) tp[++p]=sa[i]-w; Qsort(); swap(tp,rak); rak[sa[1]]=1;p=1; for(int i=2;i<=N;i++) rak[sa[i]] = (tp[sa[i]]==tp[sa[i-1]]&&tp[sa[i]+w]==tp[sa[i-1]+w])?p:++p; } int j,k=0; for(int i=1;i<=N;height[rak[i++]]=k) for(k=k?k-1:k,j=sa[rak[i]-1];a[i+k]==a[j+k];++k ); for(int i=0;i<=N;i++) { for(int j=height[i]+1;;j++) { int tot=1; for(int k=i+1;height[k]>=j;++k,++tot); if(tot>1) printf("%d\n",tot); else break; } } } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif int Meiyong; cin>>Meiyong; scanf("%s",s); N=strlen(s); for(int i=1;i<=N;i++) a[i]=s[i-1]; Ssort(); return 0; }
后缀自动机

// luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<vector> #define LL long long using namespace std; const int MAXN = 2 * 1e6 + 10; char s[MAXN]; int N; int last = 1, root = 1, tot = 1, fa[MAXN], ch[MAXN][26], len[MAXN], siz[MAXN]; void insert(int x) { int now = ++tot, pre = last; last = now; //last代表全串的点,这里不能简单的写tot - 1,因为当第三种情况时候会增加新的节点 len[now] = len[pre] + 1; siz[now] = 1; //在新加入节点后,最长的后缀的right集合大小肯定为1 for(; pre && !ch[pre][x]; pre = fa[pre]) ch[pre][x] = now; if(!pre) fa[now] = root; else { int q = ch[pre][x];//q是pre的祖先 pre -> q //说明pre有一条x转移边 q = pre + x if(len[q] == len[pre] + 1) fa[now] = q; else {//right集合不完全重合 int nows = ++tot; len[nows] = len[pre] + 1; //这里的nows用于接收len[q] <= len[pre] + 1的点 //q用于接收len[q] > len[pre] + 1 的点 memcpy(ch[nows], ch[q], sizeof(ch[q])); //这里ch[q]能转移到的,ch[nows]也一定能转移到,因为ch[nows]表示ch[q]去掉前几个字符后的串 fa[nows] = fa[q]; fa[q] = fa[now] = nows; //以前的fa[q]满足max[fa[q]] = min[q] + 1,而nows表示的串长度一定包含q里面最小的,因此fa[nows]的爸爸就是fa[q] //此时的nows表示的节点一定是q,now表示的节点的后缀, for(; pre && ch[pre][x] == q; pre = fa[pre]) ch[pre][x] = nows; //此时的pre保证可以走到q,那么pre的祖先一定是pre的后缀,他们的长度一定都是小于等于nows的 } } } vector<int> v[MAXN]; LL ans = 0; void dfs(int x) { for(int i = 0; i < v[x].size(); i++) { int to = v[x][i]; dfs(to), siz[x] += siz[to]; } //是否存在父亲出现了但是儿子没出现的情况? if(siz[x] > 1) ans = max(ans, 1ll * siz[x] * len[x]); } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); #endif scanf("%s", s + 1); N = strlen(s + 1); for(int i = 1; i <= N; i++) insert(s[i] - 'a'); for(int i = 2; i <= tot; i++) v[fa[i]].push_back(i); dfs(root); printf("%lld", ans); return 0; }
AC自动机

// luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<queue> #include<vector> using namespace std; const int MAXN = 1e6 + 10, B = 26; int T; char s[201][75], a[MAXN]; int N; int fail[MAXN], ch[MAXN][27], val[MAXN], root = 0, tot = 0, sum[MAXN]; void insert(char *s, int I) { int N = strlen(s + 1); int now = root; for(int i = 1; i <= N; i++) { int x = s[i] - 'a'; if(!ch[now][x]) ch[now][x] = ++tot; now = ch[now][x]; } val[now] = I; } void GetFail() { queue<int> q; for(int i = 0; i < B; i++) if(ch[root][i]) q.push(ch[root][i]); while(!q.empty()) { int p = q.front(); q.pop(); for(int i = 0; i < B; i++) if(ch[p][i]) fail[ch[p][i]] = ch[fail[p]][i], q.push(ch[p][i]); else ch[p][i] = ch[fail[p]][i]; } } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); #endif while(scanf("%d", &T) && T) { memset(fail, 0, sizeof(fail)); memset(ch, 0, sizeof(ch)); memset(val, 0, sizeof(val)); memset(fail, 0, sizeof(fail)); memset(sum, 0, sizeof(sum)); memset(s, 0, sizeof(s)); for(int i = 1; i <= T; i++) scanf("%s", s[i] + 1), insert(s[i], i); GetFail(); scanf("%s", a + 1); int N = strlen(a + 1), now = root; for(int i = 1; i <= N; i++) { now = ch[now][a[i] - 'a']; for(int t = now; t; t = fail[t]) if(val[t]) sum[val[t]]++; } int ans = 0; for(int i = 1; i <= T; i++) ans = max(ans, sum[i]); printf("%d\n", ans); for(int i = 1; i <= T; i++) if(sum[i] == ans) printf("%s\n", s[i] + 1); } return 0; }
数据结构
堆

1 struct S 2 { 3 int pos,val; 4 S(){ pos=0;val=0; } 5 S(int a,int b){ pos=a,val=b; } 6 7 }; 8 bool operator <(const S &a,const S &b) 9 { 10 return a.pos>b.pos; 11 }//按照位置从小到大排序 12 priority_queue<S>q;
单调队列
https://www.luogu.org/problem/show?pid=1886

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<deque> 6 using namespace std; 7 const int MAXN=1000010; 8 inline void read(int &n) 9 { 10 char c=getchar();n=0;bool flag=0; 11 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 12 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 13 } 14 struct node 15 { 16 int pos,val; 17 node(){pos=val=0;} 18 node(int a,int b) { pos=a;val=b; } 19 }; 20 deque<node>q; 21 int a[MAXN]; 22 int main() 23 { 24 int n,k; 25 read(n);read(k); 26 for(int i=1;i<=n;i++) read(a[i]); 27 for(int i=1;i<=n;i++) 28 { 29 while(q.size()>0&&q.front().pos<=(i-k)) q.pop_front(); 30 while(q.size()>0&&a[i]<q.back().val) q.pop_back(); 31 q.push_back(node(i,a[i])); 32 if(i>=k) printf("%d ",q.front().val); 33 } 34 printf("\n"); 35 while(q.size()!=0) q.pop_front(); 36 for(int i=1;i<=n;i++) 37 { 38 while(q.size()>0&&q.front().pos<=(i-k)) q.pop_front(); 39 while(q.size()>0&&a[i]>q.back().val) q.pop_back(); 40 q.push_back(node(i,a[i])); 41 if(i>=k) printf("%d ",q.front().val); 42 } 43 return 0; 44 }
线段树
单点修改&&区间求和http://codevs.cn/problem/1080/

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define ls k<<1 6 #define rs k<<1|1 7 using namespace std; 8 const int MAXN=400400; 9 inline void read(int &n) 10 { 11 char c=getchar();n=0;bool flag=0; 12 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 13 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 14 } 15 struct node 16 { 17 int l,r,w,f; 18 }tree[MAXN]; 19 int ans=0; 20 inline void update(int k) 21 { tree[k].w=tree[ls].w+tree[rs].w; } 22 inline void Build_Tree(int ll,int rr,int k) 23 { 24 tree[k].l=ll;tree[k].r=rr; 25 if(ll==rr) 26 { read(tree[k].w); return ; } 27 int mid=tree[k].l+tree[k].r>>1; 28 Build_Tree(ll,mid,ls); Build_Tree(mid+1,rr,rs); 29 update(k); 30 } 31 void Point_Add(int k,int pos,int val) 32 { 33 if(tree[k].l==tree[k].r) 34 { tree[k].w+=val; return ; } 35 int mid= tree[k].l+tree[k].r>>1; 36 if(pos<=mid) Point_Add(ls,pos,val); 37 else Point_Add(rs,pos,val); 38 update(k); 39 } 40 void Interval_Sum(int k,int ll,int rr) 41 { 42 if(ll<=tree[k].l&&tree[k].r<=rr) 43 { ans+=tree[k].w; return ; } 44 int mid=tree[k].l+tree[k].r>>1; 45 if(ll<=mid) Interval_Sum(ls,ll,rr); 46 if(rr>mid) Interval_Sum(rs,ll,rr); 47 } 48 int main() 49 { 50 int n,m; 51 read(n); 52 Build_Tree(1,n,1); 53 read(m); 54 for(int i=1;i<=m;i++) 55 { 56 int how;read(how); 57 if(how==1) 58 { 59 int pos,val; read(pos);read(val); 60 Point_Add(1,pos,val); 61 } 62 else 63 { 64 int a,b;read(a);read(b); ans=0; 65 Interval_Sum(1,a,b); 66 printf("%d\n",ans); 67 } 68 } 69 return 0; 70 }
区间修改&&区间求和http://codevs.cn/problem/1082/

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define ls k<<1 6 #define rs k<<1|1 7 #define LL long long 8 using namespace std; 9 const LL MAXN=800400; 10 inline void read(LL &n) 11 { 12 char c=getchar();n=0;bool flag=0; 13 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 14 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 15 } 16 struct node 17 { 18 LL l,r,w,f; 19 }tree[MAXN]; 20 LL ans=0; 21 inline void update(LL k) 22 { tree[k].w=tree[ls].w+tree[rs].w; } 23 inline void Build_Tree(LL ll,LL rr,LL k) 24 { 25 tree[k].l=ll;tree[k].r=rr; 26 if(ll==rr) 27 { read(tree[k].w); return ; } 28 LL mid=tree[k].l+tree[k].r>>1; 29 Build_Tree(ll,mid,ls); Build_Tree(mid+1,rr,rs); 30 update(k); 31 } 32 inline void down(LL k) 33 { 34 tree[ls].w+=(tree[ls].r-tree[ls].l+1)*tree[k].f; 35 tree[rs].w+=(tree[rs].r-tree[rs].l+1)*tree[k].f; 36 tree[ls].f+=tree[k].f; 37 tree[rs].f+=tree[k].f; 38 tree[k].f=0; 39 } 40 inline void Interval_Add(LL k,LL ll,LL rr,LL val) 41 { 42 if(ll<=tree[k].l&&tree[k].r<=rr) 43 { 44 tree[k].w+=(tree[k].r-tree[k].l+1)*val; 45 tree[k].f+=val; 46 return ; 47 } 48 if(tree[k].f) down(k); 49 LL mid=tree[k].l+tree[k].r>>1; 50 if(ll<=mid) Interval_Add(ls,ll,rr,val); 51 if(rr>mid) Interval_Add(rs,ll,rr,val); 52 update(k); 53 } 54 inline void Interval_Sum(LL k,LL ll,LL rr) 55 { 56 if(ll<=tree[k].l&&tree[k].r<=rr) 57 { 58 ans+=tree[k].w; 59 return ; 60 } 61 if(tree[k].f) down(k); 62 LL mid=tree[k].l+tree[k].r>>1; 63 if(ll<=mid) Interval_Sum(ls,ll,rr); 64 if(rr>mid) Interval_Sum(rs,ll,rr); 65 } 66 int main() 67 { 68 LL n,m; 69 read(n); 70 Build_Tree(1,n,1); 71 read(m); 72 for(LL i=1;i<=m;i++) 73 { 74 LL how;read(how); 75 if(how==1) 76 { 77 LL x,y,val;read(x);read(y);read(val); 78 Interval_Add(1,x,y,val); 79 } 80 else 81 { 82 LL x,y;read(x);read(y); 83 ans=0; 84 Interval_Sum(1,x,y); 85 printf("%lld\n",ans); 86 } 87 } 88 return 0; 89 }
区间修改&&单点修改http://codevs.cn/problem/1081/

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define ls k<<1 6 #define rs k<<1|1 7 using namespace std; 8 const int MAXN=400400; 9 inline void read(int &n) 10 { 11 char c=getchar();n=0;bool flag=0; 12 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 13 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 14 } 15 struct node 16 { 17 int l,r,w,f; 18 }tree[MAXN]; 19 int ans=0; 20 inline void update(int k) 21 { tree[k].w=tree[ls].w+tree[rs].w; } 22 inline void Build_Tree(int ll,int rr,int k) 23 { 24 tree[k].l=ll;tree[k].r=rr; 25 if(ll==rr) 26 { read(tree[k].w); return ; } 27 int mid=tree[k].l+tree[k].r>>1; 28 Build_Tree(ll,mid,ls); Build_Tree(mid+1,rr,rs); 29 update(k); 30 } 31 inline void down(int k) 32 { 33 tree[ls].w+=(tree[ls].r-tree[ls].l+1)*tree[k].f; 34 tree[rs].w+=(tree[rs].r-tree[rs].l+1)*tree[k].f; 35 tree[ls].f+=tree[k].f; 36 tree[rs].f+=tree[k].f; 37 tree[k].f=0; 38 update(k); 39 return ; 40 } 41 void Interval_Add(int k,int ll,int rr,int val) 42 { 43 if(ll<=tree[k].l&&tree[k].r<=rr) 44 { 45 tree[k].w=tree[k].w+(tree[k].r-tree[k].l+1)*val; 46 tree[k].f+=val; 47 return ; 48 } 49 if(tree[k].f) down(k); 50 int mid=tree[k].l+tree[k].r>>1; 51 if(ll<=mid) Interval_Add(ls,ll,rr,val); 52 if(rr>mid) Interval_Add(rs,ll,rr,val); 53 update(k); 54 } 55 void Point_Ask(int k,int pos) 56 { 57 if(tree[k].l==tree[k].r) 58 { 59 ans=tree[k].w; 60 return ; 61 } 62 if(tree[k].f) down(k); 63 int mid=tree[k].l+tree[k].r>>1; 64 if(pos<=mid) Point_Ask(ls,pos); 65 else Point_Ask(rs,pos); 66 } 67 int main() 68 { 69 int n,m; 70 read(n); 71 Build_Tree(1,n,1); 72 read(m); 73 for(int i=1;i<=m;i++) 74 { 75 int how;read(how); 76 if(how==1) 77 { 78 int x,y,val;read(x);read(y);read(val); 79 Interval_Add(1,x,y,val); 80 } 81 else 82 { 83 int pos;read(pos); 84 ans=0; 85 Point_Ask(1,pos); 86 printf("%d\n",ans); 87 } 88 } 89 return 0; 90 }
区间修改&&区间覆盖&&区间求和&&最大值&&&最小值http://codevs.cn/problem/4927/

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define LL long long 6 #define ls k<<1 7 #define rs k<<1|1 8 using namespace std; 9 const LL MAXN=400400; 10 const LL INF =0x7fffff; 11 inline void read(LL &n) 12 { 13 char c=getchar();n=0;bool flag=0; 14 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 15 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 16 } 17 struct node 18 { 19 LL l,r,w,Max,Min,Set,Add; 20 bool V; 21 }tree[MAXN]; 22 LL n,m; 23 LL ans=0; 24 inline void update(LL k) 25 { 26 tree[k].w=tree[ls].w+tree[rs].w; 27 tree[k].Max=max(tree[ls].Max,tree[rs].Max); 28 tree[k].Min=min(tree[ls].Min,tree[rs].Min); 29 } 30 void Build_Tree(LL ll,LL rr,LL k) 31 { 32 tree[k].l=ll;tree[k].r=rr; 33 if(tree[k].l==tree[k].r) 34 { 35 read(tree[k].w); 36 tree[k].Max=tree[k].w; 37 tree[k].Min=tree[k].w; 38 return ; 39 } 40 LL mid=tree[k].l+tree[k].r>>1; 41 Build_Tree(ll,mid,ls); 42 Build_Tree(mid+1,rr,rs); 43 update(k); 44 } 45 void down(LL k) 46 { 47 if(tree[k].V) 48 { 49 tree[ls].Add=0; 50 tree[ls].V=1; 51 tree[ls].w=(tree[ls].r-tree[ls].l+1)*tree[k].Set; 52 tree[ls].Max=tree[ls].Min=tree[ls].Set=tree[k].Set; 53 54 tree[rs].Add=0; 55 tree[rs].V=1; 56 tree[rs].w=(tree[rs].r-tree[rs].l+1)*tree[k].Set; 57 tree[rs].Max=tree[rs].Min=tree[rs].Set=tree[k].Set; 58 59 tree[k].Set=tree[k].V=0; 60 } 61 if(tree[k].Add) 62 { 63 tree[ls].w+=(tree[ls].r-tree[ls].l+1)*tree[k].Add; 64 tree[ls].Add+=tree[k].Add; 65 tree[ls].Max+=tree[k].Add; 66 tree[ls].Min+=tree[k].Add; 67 68 tree[rs].w+=(tree[rs].r-tree[rs].l+1)*tree[k].Add; 69 tree[rs].Add+=tree[k].Add; 70 tree[rs].Max+=tree[k].Add; 71 tree[rs].Min+=tree[k].Add; 72 tree[k].Add=0; 73 } 74 75 } 76 void Interval_Add(LL k,LL ll,LL rr,LL val) 77 { 78 if(ll<=tree[k].l&&tree[k].r<=rr) 79 { 80 tree[k].w+=(tree[k].r-tree[k].l+1)*val; 81 tree[k].Add+=val; 82 tree[k].Max+=val; 83 tree[k].Min+=val; 84 return ; 85 } 86 if(tree[k].Add||tree[k].V) down(k); 87 LL mid=tree[k].r+tree[k].l>>1; 88 if(ll<=mid) Interval_Add(ls,ll,rr,val); 89 if(rr>mid) Interval_Add(rs,ll,rr,val); 90 update(k); 91 } 92 void Interval_Change(LL k,LL ll,LL rr,LL val) 93 { 94 if(ll<=tree[k].l&&tree[k].r<=rr) 95 { 96 tree[k].Max=tree[k].Min=val; 97 tree[k].Set=val;tree[k].V=1; 98 tree[k].w=(tree[k].r-tree[k].l+1)*val; 99 tree[k].Add=0; 100 return ; 101 } 102 if(tree[k].Add||tree[k].V) down(k); 103 LL mid=tree[k].r+tree[k].l>>1; 104 if(ll<=mid) Interval_Change(ls,ll,rr,val); 105 if(rr>mid) Interval_Change(rs,ll,rr,val); 106 update(k); 107 } 108 void Interval_Sum(LL k,LL ll,LL rr) 109 { 110 if(ll<=tree[k].l&&tree[k].r<=rr) 111 { 112 ans+=tree[k].w; 113 return ; 114 } 115 if(tree[k].Add||tree[k].V) down(k); 116 LL mid=tree[k].r+tree[k].l>>1; 117 if(ll<=mid) Interval_Sum(ls,ll,rr); 118 if(rr>mid) Interval_Sum(rs,ll,rr); 119 } 120 void Interval_Max(LL k,LL ll,LL rr) 121 { 122 if(ll<=tree[k].l&&tree[k].r<=rr) 123 { 124 ans=max(ans,tree[k].Max); 125 return ; 126 } 127 if(tree[k].Add||tree[k].V) down(k); 128 LL mid=tree[k].r+tree[k].l>>1; 129 if(ll<=mid) Interval_Max(ls,ll,rr); 130 if(rr>mid) Interval_Max(rs,ll,rr); 131 } 132 void Interval_Min(LL k,LL ll,LL rr) 133 { 134 if(ll<=tree[k].l&&tree[k].r<=rr) 135 { 136 ans=min(ans,tree[k].Min); 137 return ; 138 } 139 if(tree[k].Add||tree[k].V) down(k); 140 LL mid=tree[k].r+tree[k].l>>1; 141 if(ll<=mid) Interval_Min(ls,ll,rr); 142 if(rr>mid) Interval_Min(rs,ll,rr); 143 } 144 int main() 145 { 146 read(n);read(m); 147 Build_Tree(1,n,1); 148 for(LL i=1;i<=m;i++) 149 { 150 char how[5]; 151 scanf("%s",how); 152 if(how[0]=='a')//区间加 153 { 154 LL x,y,val;read(x);read(y);read(val); 155 Interval_Add(1,x,y,val); 156 } 157 else if(how[0]=='s'&&how[1]=='e')//区间赋值 158 { 159 LL x,y,val;read(x);read(y);read(val); 160 Interval_Change(1,x,y,val); 161 } 162 else if(how[0]=='s'&&how[1]=='u')//区间求和 163 { 164 LL x,y;read(x);read(y);ans=0; 165 Interval_Sum(1,x,y); 166 printf("%lld\n",ans); 167 } 168 else if(how[0]=='m'&&how[1]=='a')//区间最大值 169 { 170 LL x,y;read(x);read(y);ans=0; 171 Interval_Max(1,x,y); 172 printf("%lld\n",ans); 173 } 174 else if(how[0]=='m'&&how[1]=='i')// 区间最小值 175 { 176 LL x,y;read(x);read(y);ans=INF; 177 Interval_Min(1,x,y); 178 printf("%lld\n",ans); 179 } 180 } 181 return 0; 182 }
区间乘区间加区间修改

// luogu-judger-enable-o2 // luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<cstdio> #include<cmath> #include<algorithm> #define ls k<<1 #define rs k<<1|1 #define int long long using namespace std; const int MAXN=1e6+10; inline int read() { char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int N,M,mod; namespace SegmentTree { struct node { int mul,add,sum,l,r,siz; }T[MAXN]; void update(int k) { T[k].sum=(T[ls].sum%mod+T[rs].sum%mod)%mod; } void ps(int x,int f) { T[x].mul=(T[x].mul%mod*T[f].mul%mod)%mod; T[x].add=(T[x].add*T[f].mul)%mod; T[x].add=(T[x].add+T[f].add)%mod; T[x].sum=(T[x].sum%mod*T[f].mul%mod)%mod; T[x].sum=(T[x].sum+T[f].add%mod*T[x].siz)%mod; } void pushdown(int k) { if(T[k].add==0&&T[k].mul==1) return ; ps(ls,k); ps(rs,k); T[k].add=0; T[k].mul=1; } void Build(int k,int ll,int rr) { T[k].l=ll;T[k].r=rr;T[k].siz=rr-ll+1;T[k].mul=1; if(ll==rr) { T[k].sum=read()%mod; return ; } int mid=ll+rr>>1; Build(ls,ll,mid); Build(rs,mid+1,rr); update(k); } void IntervalMul(int k,int ll,int rr,int val) { if(ll<=T[k].l&&T[k].r<=rr) { T[k].sum=(T[k].sum*val)%mod; T[k].mul=(T[k].mul*val)%mod; T[k].add=(T[k].add*val)%mod; return ; } pushdown(k); int mid=T[k].l+T[k].r>>1; if(ll<=mid) IntervalMul(ls,ll,rr,val); if(rr>mid) IntervalMul(rs,ll,rr,val); update(k); } void IntervalAdd(int k,int ll,int rr,int val) { if(ll<=T[k].l&&T[k].r<=rr) { T[k].sum=(T[k].sum+T[k].siz*val)%mod; T[k].add=(T[k].add+val)%mod; return ; } pushdown(k); int mid=T[k].l+T[k].r>>1; if(ll<=mid) IntervalAdd(ls,ll,rr,val); if(rr>mid) IntervalAdd(rs,ll,rr,val); update(k); } int IntervalSum(int k,int ll,int rr) { int ans=0; if(ll<=T[k].l&&T[k].r<=rr) { ans=(ans+T[k].sum)%mod; return ans; } pushdown(k); int mid=T[k].l+T[k].r>>1; if(ll<=mid) ans=(ans+IntervalSum(ls,ll,rr))%mod; if(rr>mid) ans=(ans+IntervalSum(rs,ll,rr))%mod; return ans%mod; } } main() { #ifdef WIN32 freopen("a.in","r",stdin); #endif N=read();M=read();mod=read(); SegmentTree::Build(1,1,N); while(M--) { int opt=read(); if(opt==1) { int l=read(),r=read(),val=read()%mod; SegmentTree::IntervalMul(1,l,r,val); } else if(opt==2) { int l=read(),r=read(),val=read()%mod; SegmentTree::IntervalAdd(1,l,r,val); } else if(opt==3) { int l=read(),r=read(); printf("%lld\n", SegmentTree::IntervalSum(1,l,r)%mod); } } return 0; }
树状数组
单点修改&&区间查询https://www.luogu.org/problem/show?pid=3374

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define lb(x) (x&(-x)) 6 using namespace std; 7 const int MAXN=500001; 8 inline int read() 9 { 10 char c=getchar();int x=0;int f=1; 11 while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();} 12 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*f; 13 } 14 int tree[MAXN]; 15 int n=read(),m=read(); 16 inline void Point_Add(int pos,int val) 17 { 18 while(pos<=n) tree[pos]+=val,pos+=lb(pos); 19 } 20 inline int Interval_Sum(int pos) 21 { 22 int ans=0; 23 while(pos) ans+=tree[pos], pos-=lb(pos); 24 return ans; 25 } 26 int main() 27 { 28 29 for(int i=1;i<=n;i++) 30 { 31 int p=read();Point_Add(i,p); 32 } 33 for(int i=1;i<=m;i++) 34 { 35 int how=read(),x=read(),y=read(); 36 if(how==1) Point_Add(x,y); 37 else printf("%d\n",Interval_Sum(y)-Interval_Sum(x-1)); 38 } 39 return 0; 40 }
区间修改&&单点查询https://www.luogu.org/problem/show?pid=3368

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define lb(x) (x&(-x)) 6 using namespace std; 7 const int MAXN=500001; 8 inline int read() 9 { 10 char c=getchar();int x=0;int f=1; 11 while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();} 12 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*f; 13 } 14 int tree[MAXN]; 15 int n=read(),m=read(); 16 inline void Point_Add(int pos,int val) 17 { 18 while(pos<=n) tree[pos]+=val,pos+=lb(pos); 19 } 20 inline int Interval_Sum(int pos) 21 { 22 int ans=0; 23 while(pos) ans+=tree[pos], pos-=lb(pos); 24 return ans; 25 } 26 int main() 27 { 28 int pre=0; 29 for(int i=1;i<=n;i++) 30 { 31 int p=read();Point_Add(i,p-pre); 32 pre=p; 33 } 34 for(int i=1;i<=m;i++) 35 { 36 int how=read(),x=read(),y,val; 37 if(how==1) y=read(),val=read(),Point_Add(x,val),Point_Add(y+1,-val); 38 else printf("%d\n",Interval_Sum(x)); 39 } 40 return 0; 41 }
平衡树
splay

#include<cstdio> #include<algorithm> using namespace std; const int MAXN = 4 * 1e5 + 10, INF = 1e9; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int T; #define ls(x) ch[x][0] #define rs(x) ch[x][1] #define root ch[0][1] int ch[MAXN][2], fa[MAXN], rev[MAXN], siz[MAXN], val[MAXN], tot = 0; int ident(int x) { return ch[fa[x]][0] == x ? 0 : 1;} void connect(int x, int _fa, int how) { fa[x] = _fa; ch[fa[x]][how] = x;} void update(int x) { siz[x] = siz[ls(x)] + siz[rs(x)] + rev[x];} void rotate(int x) { int Y = fa[x], R = fa[Y]; int Yson = ident(x), Rson = ident(Y); int B = ch[x][Yson ^ 1]; connect(x, R, Rson); connect(Y, x, Yson ^ 1); connect(B, Y, Yson); update(Y); update(x); } void splay(int x, int to) { to = fa[to]; while(fa[x] != to) { int y = fa[x]; if(fa[y] == to) rotate(x); else if(ident(x) == ident(y)) rotate(y), rotate(x); else rotate(x), rotate(x); } } int NewNode(int _fa, int v) { fa[++tot]= _fa; siz[tot] = rev[tot] = 1; val[tot] = v; return tot; } void insert(int v) { if(root == 0) {root = NewNode(0, v); return ;} int now = root; while(now) { siz[now]++; if(val[now] == v) {rev[now]++; splay(now, root); return ;} int nxt = v > val[now]; if(!ch[now][nxt]) {ch[now][nxt] = NewNode(now, v); splay(now, root); return ;} now = ch[now][nxt]; } } int find(int v) { int now = root; while(now) { if(val[now] == v) {splay(now, root); return now;} int nxt = v > val[now]; now = ch[now][nxt]; } } void erase(int v) { int now = find(v); if(rev[now] > 1) {rev[now]--; siz[now]--; return ;} else if(!ls(now) && !rs(now)) {root = 0; return ;} else if(!ls(now)) {root = rs(now); fa[rs(now)] = 0;} else { int l = ls(now); while(rs(l)) l = rs(l); splay(l, ls(now)); //ch[l][1] = rs(now); fa[rs(now)] = l; connect(rs(now), l, 1); connect(l, 0, 1); update(l); } } int rak(int v) { int pos = find(v); return siz[ch[pos][0]] + 1; } int kth(int v) { int now = root; while(now) { int used = siz[now] - siz[rs(now)]; if(v <= used && v > siz[ls(now)]) return val[now]; if(v > used) now = ch[now][1], v -= used; else now = ch[now][0]; } } int pre(int v) { int ans = -INF, now = root; while(now) { if(val[now] < v) ans = max(ans, val[now]); int nxt = v <= val[now] ? 0 : 1; now = ch[now][nxt]; } return ans; } int nxt(int v) { int ans = INF, now = root; while(now) { if(val[now] > v) ans = min(ans, val[now]); int nxt = v < val[now] ? 0 : 1; now = ch[now][nxt]; } return ans; } int main() { T = read(); while(T--) { int opt = read(), x = read(); if(opt == 1) insert(x); else if(opt == 2) erase(x); else if(opt == 3) printf("%d\n", rak(x)); else if(opt == 4) printf("%d\n", kth(x)); else if(opt == 5) printf("%d\n", pre(x)); else if(opt == 6) printf("%d\n", nxt(x)); } return 0; }
Treap

#include<iostream> #include<cstdio> #include<cstdlib> #define ls tree[k].l #define rs tree[k].r using namespace std; const int MAXN=1e6+10; inline char nc() { static char buf[MAXN],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin))?EOF:*p1++; } inline int read() { char c=nc();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=nc();} while(c>='0'&&c<='9'){x=x*10+c-'0',c=nc();} return x*f; } struct node { int l,r,tot,recy,val,rd; }tree[MAXN]; int size,root,ans=0; inline void update(int k) { tree[k].tot=tree[ls].tot+tree[rs].tot+tree[k].recy; } inline void insert(int &k,int x) { if(k==0) { ++size;k=size; tree[size].recy=tree[size].tot=1; tree[size].val=x;tree[size].rd=rand();return ; } tree[k].tot++; if(tree[k].val==x) tree[k].recy++; else if(x < tree[k].val) insert( ls, x); else insert( rs , x ); } inline void LeftRotate(int &k) { int R=tree[k].r; tree[k].r=tree[R].l; tree[R].l=k; tree[R].tot=tree[k].tot; update(k);k=R; } inline void RightRotate(int &k) { int R=tree[k].l; tree[k].l=tree[R].r; tree[R].r=k; tree[R].tot=tree[k].tot; update(k);k=R; } inline void del(int &k,int x) { if(!k) return ; if(tree[k].val==x) { if(tree[k].recy>1) {tree[k].recy-=1,tree[k].tot-=1;return; } if(tree[k].l*tree[k].r==0) k=tree[k].l+tree[k].r; else if(tree[ls].rd<tree[rs].rd) RightRotate(k),del(k,x); else LeftRotate(k),del(k,x); } else if(x>tree[k].val) tree[k].tot--,del(rs,x); else tree[k].tot--,del(ls,x); } int atrank(int &k,int x) { if(k==0) return 0; if(tree[k].val==x) return tree[ls].tot+1; if(tree[k].val<x) return atrank(rs,x)+tree[ls].tot+tree[k].recy; else return atrank(ls,x); } int rerand(int k,int x) { if(k==0) return 0; if(x<=tree[ls].tot) return rerand(ls,x); else if(x>tree[ls].tot+tree[k].recy) return rerand(rs,x-tree[ls].tot-tree[k].recy); else return tree[k].val; } void pred(int k,int x) { if(k==0) return ; if(tree[k].val<x) ans=k,pred(rs,x); else pred(ls,x); } void succ(int &k,int x) { if(k==0) return ; if(tree[k].val>x) ans=k,succ(ls,x); else succ(rs,x); } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif int n=read(); while(n--) { int opt=read(),x=read();ans=0; if(opt==1) insert(root,x); if(opt==2) del(root,x); if(opt==3) printf("%d\n",atrank(root,x)); if(opt==4) printf("%d\n",rerand(root,x)); if(opt==5) {pred(root,x);printf("%d\n",tree[ans].val);} if(opt==6) {succ(root,x);printf("%d\n",tree[ans].val);} } }
FHQ Treap

#include<iostream> #include<cstdio> #include<cstring> #include<ctime> #include<cstdlib> using namespace std; #define ls T[now].ch[0] #define rs T[now].ch[1] const int MAXN=1e6+10; inline char nc() { static char buf[MAXN],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin),p1==p2)?EOF:*p1++; } inline int read() { char c=nc();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=nc();} while(c>='0'&&c<='9'){x=x*10+c-'0',c=nc();} return x*f; } struct node { int ch[2],val,siz,pri; }T[MAXN]; int tot=0; int x,y,z,root=0; int newnode(int v) { T[++tot].siz=1; T[tot].val=v; T[tot].pri=rand(); return tot; } void update(int now) { T[now].siz=T[ls].siz+T[rs].siz+1; } void split(int now,int k,int &x,int &y) { if(!now) {x=y=0;return ;} if(T[now].val<=k) x=now,split(rs,k,rs,y); else y=now,split(ls,k,x,ls); update(now); } int merge(int x,int y) { if(!x||!y) return x+y; if(T[x].pri<T[y].pri) { T[x].ch[1]=merge(T[x].ch[1],y); update(x); return x; } else { T[y].ch[0]=merge(x,T[y].ch[0]); update(y); return y; } } int kth(int now,int x) { while(1) { if(T[ls].siz>=x) now=ls; else if(T[ls].siz+1==x) return now; else x-=T[ls].siz+1,now=rs; } } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif srand((unsigned)time(NULL)); int n=read(); while(n--) { int opt=read(),val=read(); if(opt==1) { split(root,val,x,y); root=merge( merge(x,newnode(val)),y ); } else if(opt==2) { split(root,val,x,z); split(x,val-1,x,y); y=merge(T[y].ch[0],T[y].ch[1]); root=merge( merge(x,y) ,z); } else if(opt==3) { split(root,val-1,x,y); printf("%d\n",T[x].siz+1); root=merge(x,y); } else if(opt==4) { printf("%d\n",T[kth(root,val)].val); } else if(opt==5) { split(root,val-1,x,y); printf("%d\n",T[kth(x,T[x].siz)].val); root=merge(x,y); } else if(opt==6) { split(root,val,x,y); printf("%d\n",T[kth(y,1)].val); root=merge(x,y); } } return 0; } FHQ Treap
Trie树
01 Trie
http://www.cnblogs.com/zwfymqz/p/8440398.html

#include<cstdio> #include<cmath> #include<algorithm> using namespace std; const int MAXN=1e6+10; inline int read() { char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } #define debug(x) printf("%d",x); struct node { int val,ch[2]; node(){val=ch[0]=ch[1]=0;} void clear(){val=ch[0]=ch[1]=0;} }T[MAXN]; int a[MAXN],root=0,tot=0; void Insert(int v) { int now=root; for(int i=31;i>=0;i--) { int opt=(v&(1<<i))?1:0; if(!T[now].ch[opt]) T[now].ch[opt]=++tot; now=T[now].ch[opt]; T[now].val++; } } void Delet(int v) { int now=root; for(int i=31;i>=0;i--) { int opt=(v&(1<<i))?1:0; now=T[now].ch[opt]; T[now].val--; } } int Query(int v) { int ans=0,now=root; for(int i=31;i>=0;i--) { int opt=(v&(1<<i))?1:0; if(T[T[now].ch[opt^1]].val) ans+=1<<i,now=T[now].ch[opt^1]; else now=T[now].ch[opt]; } return ans; } int main() { freopen("a.in","r",stdin); int Test=read(); while(Test--) { int N=read(); for(int i=1;i<=N;i++) a[i]=read(); for(int i=1;i<=4*N;i++) T[i].clear(); for(int i=1;i<=N;i++) Insert(a[i]); int ans=0; for(int i=1;i<=N;i++) { for(int j=1;j<i;j++) { Delet(a[i]);Delet(a[j]); ans=max(ans,Query(a[i]+a[j])); Insert(a[i]);Insert(a[j]); } } printf("%d\n",ans); } return 0; }
杂类算法
树上倍增
https://www.luogu.org/problem/show?pid=3379

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 using namespace std; 6 const int MAXN=1000001; 7 inline void read(int &n) 8 { 9 char c=getchar();bool flag=0;n=0; 10 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 11 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 12 } 13 struct node 14 { 15 int u,v,nxt; 16 }edge[MAXN]; 17 int head[MAXN]; 18 int num=1; 19 inline void add_edge(int x,int y) 20 { 21 edge[num].u=x; 22 edge[num].v=y; 23 edge[num].nxt=head[x]; 24 head[x]=num++; 25 } 26 int deep[MAXN]; 27 int f[MAXN][21]; 28 int n,m,root; 29 int dfs(int now) 30 { 31 for(int i=head[now];i!=-1;i=edge[i].nxt) 32 if(deep[edge[i].v]==0) 33 deep[edge[i].v]=deep[now]+1,f[edge[i].v][0]=now,dfs(edge[i].v); 34 } 35 int pre() 36 { 37 for(int i=1;i<=19;i++) 38 for(int j=1;j<=n;j++) 39 f[j][i]=f[f[j][i-1]][i-1]; 40 } 41 int LCA(int x,int y) 42 { 43 if(deep[x]<deep[y]) swap(x,y); 44 for(int i=19;i>=0;i--) 45 if(deep[f[x][i]]>=deep[y]) 46 x=f[x][i]; 47 if(x==y) return x; 48 for(int i=19;i>=0;i--) 49 if(f[x][i]!=f[y][i]) 50 x=f[x][i],y=f[y][i]; 51 return f[x][0]; 52 } 53 int main() 54 { 55 memset(head,-1,sizeof(head)); 56 read(n);read(m);read(root); 57 for(int i=1;i<=n-1;i++) 58 { 59 int x,y; 60 read(x);read(y);add_edge(x,y);add_edge(y,x); 61 } 62 deep[root]=1; 63 dfs(root); 64 pre(); 65 for(int i=1;i<=m;i++) 66 { 67 int x,y; 68 read(x);read(y); 69 printf("%d\n",LCA(x,y)); 70 } 71 return 0; 72 }
ST表
https://www.luogu.org/problem/show?pid=3865

// luogu-judger-enable-o2 #include<cstdio> #include<algorithm> #define max(a,b) (a<b?b:a) #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<19,stdin),p1==p2)?EOF:*p1++) char buf[1<<19],*p1=buf,*p2=buf; const int MAXN=1e5+10; inline int read() { char c=getchar();register int x=0; while(c<'0'||c>'9')c=getchar(); while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar(); return x; } char obuf[1<<24],*O=obuf; void print(int x) { if(x>9) print(x/10); *O++=x%10+'0'; } int N,M; int f[MAXN][22]; int log2[MAXN]; int Query(int l,int r) { int k=log2[r-l+1]; return max(f[l][k],f[r-(1<<k)+1][k]); } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #endif N=read();M=read(); for(int i=1;i<=N;i++) f[i][0]=read(); for(int i=2;i<=N;i++) log2[i]=log2[i>>1]+1; for(register int j=1;j<=17;j++) for(register int i=1;i<=N&&i+(1<<j)-1<=N;i++) f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); while(M--) { int l=read(),r=read(); print(Query(l,r)); *O++='\n'; } fwrite(obuf,O-obuf,1,stdout); return 0; }
点分治
给定一棵有n个点的树
询问树上距离为k的点对是否存在

#include<iostream> #include<cstdio> #include<cstring> #include<cmath> using namespace std; const int MAXN=1e6+10; const int INF=1e7+10; inline char nc() { static char buf[MAXN],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin),p1==p2)?EOF:*p1++; } inline int read() { char c=nc();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=nc();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=nc();} return x*f; } struct node { int u,v,w,nxt; }edge[MAXN]; int head[MAXN]; int num=1; inline void AddEdge(int x,int y,int z) { edge[num].u=x; edge[num].v=y; edge[num].w=z; edge[num].nxt=head[x]; head[x]=num++; } int F[MAXN],sum,siz[MAXN],vis[MAXN],root=0,cnt=0,deep[MAXN],can[MAXN]; struct Ans { int v,id; }tot[MAXN]; void GetRoot(int now,int fa) { siz[now]=1; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(vis[edge[i].v]||edge[i].v==fa) continue; GetRoot(edge[i].v,now); siz[now]+=siz[edge[i].v]; F[now]=max(F[now],siz[edge[i].v]); } F[now]=max(F[now],sum-F[now]); if(F[now]<F[root]) root=now; } void GetDeep(int now,int fa,int NowDeep,int num) { int cur=0; tot[++cnt].v=deep[now]; tot[cnt].id=num; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(vis[edge[i].v]||edge[i].v==fa) continue; deep[edge[i].v]=deep[now]+edge[i].w; if(NowDeep!=1) GetDeep(edge[i].v,now,NowDeep+1,num); else GetDeep(edge[i].v,now,NowDeep+1,cur++); } } void Work(int now) { cnt=0;deep[now]=0; GetDeep(now,0,1,1); for(int i=1;i<=cnt;i++) for(int j=i+1;j<=cnt;j++) if(tot[i].id!=tot[j].id) can[tot[i].v+tot[j].v]=1; else can[tot[i].v]=1,can[tot[j].v]=1; } void Solve(int now) { Work(now); vis[now]=1; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(vis[edge[i].v]) continue; root=0; sum=siz[edge[i].v]; GetRoot(edge[i].v,0); Solve(edge[i].v); } } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif memset(head,-1,sizeof(head)); int N=read(),M=read(); for(int i=1;i<=N-1;i++) { int x=read(),y=read(),z=read(); AddEdge(x,y,z); AddEdge(y,x,z); } root=0; F[0]=INF; sum=N; GetRoot(1,0); Solve(root); for(int i=1;i<=M;i++) { int p=read(); if(can[p]) printf("AYE\n"); else printf("NAY\n"); } return 0; }
主席树

// luogu-judger-enable-o2 // luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<cstdio> #include<algorithm> #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) char buf[1<<21],*p1=buf,*p2=buf; using namespace std; const int MAXN=4*1e6+10; inline int read() { char c=getchar();register int x=0; while(c<'0'||c>'9')c=getchar(); while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar(); return x; } char obuf[1<<24],*O=obuf; void print(int x) { if(x>9) print(x/10); *O++=x%10+'0'; } int N,M; int a[MAXN],date[MAXN]; #define ls(x) T[x].ls #define rs(x) T[x].rs struct node { int siz,ls,rs; }T[MAXN]; int root[MAXN],tot=0; void Insert(int pre,int &now,int l,int r,int pos) { if(!now) now=++tot; T[now].siz=T[pre].siz+1; if(l==r) return ; int mid=(l+r)>>1; if(pos<=mid) T[now].rs=T[pre].rs,Insert(T[pre].ls,T[now].ls,l,mid,pos); else T[now].ls=T[pre].ls,Insert(T[pre].rs,T[now].rs,mid+1,r,pos); } int Query(int pre,int now,int l,int r,int k) { if(l==r) return l; int left=T[ls(now)].siz-T[ls(pre)].siz; int mid=(l+r)>>1; if(k>left) return Query(T[pre].rs,T[now].rs,mid+1,r,k-left); else return Query(T[pre].ls,T[now].ls,l,mid,k); } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #endif N=read();M=read(); for(int i=1;i<=N;i++) date[i]=a[i]=read(); sort(date+1,date+N+1); int num=unique(date+1,date+N+1)-date-1; for(int i=1;i<=N;i++) a[i]=lower_bound(date+1,date+num+1,a[i])-date; for(int i=1;i<=N;i++) Insert(root[i-1],root[i],1,num,a[i]); for(int i=1;i<=M;i++) { int l=read(),r=read(),k=read(); print(date[Query(root[l-1],root[r],1,num,k)]); *O++='\n'; } fwrite(obuf,O-obuf,1,stdout); return 0; }
排序
归并排序

1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 using namespace std; 5 const int MAXN=100001; 6 inline int read() 7 { 8 char c=getchar();int x=0,flag=1; 9 while(c<'0'||c>'9') {if(c=='-') flag=-1;c=getchar();} 10 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*flag; 11 } 12 int n; 13 int a[MAXN]; 14 int tmp[MAXN]; 15 void Sort(int l,int r) 16 { 17 if(l==r) return ; 18 int mid=l+r>>1; 19 Sort(l,mid);Sort(mid+1,r); 20 int nowl=l,nowr=mid+1,nowpos=l; 21 while(nowl<=mid&&nowr<=r) 22 { 23 if(a[nowl]<=a[nowr]) tmp[nowpos++]=a[nowl],nowl++; 24 else tmp[nowpos++]=a[nowr],nowr++; 25 } 26 while(nowl<=mid) tmp[nowpos++]=a[nowl],nowl++; 27 while(nowr<=r) tmp[nowpos++]=a[nowr],nowr++; 28 for(int i=l;i<=r;i++) a[i]=tmp[i]; 29 } 30 int main() 31 { 32 n=read(); 33 for(int i=1;i<=n;i++) a[i]=read(); 34 Sort(1,n); 35 for(int i=1;i<=n;i++) printf("%d ",a[i]); 36 return 0; 37 }
高精度
高精加

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<stdlib.h> 6 #include<ctime> 7 using namespace std; 8 const int MAXN=100001; 9 inline int read() 10 { 11 char c=getchar();int f=1,x=0; 12 while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();} 13 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*f; 14 } 15 char a[MAXN],b[MAXN],c[MAXN]; 16 int la,lb,x=0; 17 int main() 18 { 19 scanf("%s%s",a+1,b+1); 20 la=strlen(a+1);lb=strlen(b+1); 21 for(int i=1;i<=max(la,lb);i++) 22 c[i]+=(a[i]+b[i]+x)%10,x=(a[i]+b[i]+x)/10; 23 c[max(la,lb)+1]=x; 24 bool flag=0; 25 for(int i=max(la,lb)+1;i>=1;i--) 26 if(c[i]!=0) 27 { 28 for(int j=i;j>=1;j--) printf("%d",c[j]); 29 return 0; 30 } 31 printf("0"); 32 return 0; 33 }
数论
Lucas定理
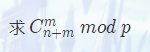

#include<cstdio> #include<algorithm> #include<cmath> #include<map> #define int long long using namespace std; const int MAXN = 4 * 1e5 + 10, mod = 100003; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int T, N, M, P; int fac[MAXN] = {1}; int fastpow(int a, int p, int mod) { int base = 1; while(p) { if(p & 1) base = (base % mod * a % mod) % mod; a = (a % mod * a % mod) % mod; p >>= 1; } return base % mod; } int inv(int a, int p) { return fastpow(a, p - 2, p); } int C(int N, int M, int P) { if(M > N) return 0; return fac[N] % P * inv(fac[M] * fac[N - M], P); } int Lucas(int N, int M, int P) { if(!N || !M) return 1; return Lucas(N / P, M / P, P) * C(N % P, M % P, P); } main() { //freopen("a.in", "r", stdin); T = read(); while(T--) { int N = read(), M = read(), P = read(); N = N + M; for(int i = 1; i <= 2 * 1e5; i++) fac[i] = (i * fac[i - 1]) % P; printf("%lld\n", Lucas(N, M, P) % P); } }
高斯消元
https://www.luogu.org/problemnew/show/P3389

// luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<cstdio> #define swap(x, y) x ^= y, y ^= x, x ^= y const int MAXN= 102; double A[MAXN][MAXN]; double Ans[MAXN]; int N; void Guess() { for(int i = 1; i <= N; i++) { int mx = i; for(int j = i + 1; j <= N; j++) if(A[j][i] > A[mx][i]) swap(mx, j); if(A[i][i] == 0) {printf("No Solution\n");return ;} for(int j = i + 1; j <= N; j++) { double tmp = A[j][i] / A[i][i]; for(int k = i + 1; k <= N + 1; k++) A[j][k] -= tmp * A[i][k]; } } for(int i = N; i >= 1; i--) { Ans[i] = A[i][N + 1] / A[i][i]; for(int j = i; j >= 1; j--) A[j][N + 1] -= A[j][i] * Ans[i]; } for(int i = 1; i <= N; i++) printf("%.2lf\n", Ans[i]); } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); #endif scanf("%d", &N); for(int i = 1; i <= N; i++) for(int j = 1; j <= N + 1; j++) scanf("%lf", &A[i][j]); Guess(); return 0; }
莫比乌斯反演
FGD正在破解一段密码,他需要回答很多类似的问题:对于给定的整数a,b和d,有多少正整数对x,y,满足x<=a,y<=b,并且gcd(x,y)=d。作为FGD的同学,FGD希望得到你的帮助。

// luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #define int long long using namespace std; const int MAXN=1e6+10; inline int read() { char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int N; int vis[MAXN],prime[MAXN],mu[MAXN],tot=0; void GetMu() { vis[1]=1;mu[1]=1; for(int i=1;i<=N;i++) { if(!vis[i]) prime[++tot]=i,mu[i]=-1; for(int j=1;j<=tot&&i*prime[j]<=N;j++) { vis[i*prime[j]]=1; if(i%prime[j]==0) {mu[i*prime[j]]=0;break;} else mu[i*prime[j]]=-mu[i]; } } for(int i=1;i<=N;i++) mu[i]+=mu[i-1]; } main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif N=1e6; GetMu(); int QWQ=read(); while(QWQ--) { int n=read(),m=read(),k=read(),ans=0; int limit=min(n/k,m/k); int nxt=0; for(int i=1;i<=limit;i=nxt+1) nxt=min(n/(n/i),m/(m/i)), ans+=(mu[nxt]-mu[i-1])*((n/k)/i)*((m/k)/i); printf("%lld\n",ans); } return 0; }
线性基

//http://acm.hdu.edu.cn/showproblem.php?pid=3949 #include<bits/stdc++.h> #define LL long long using namespace std; const int MAXN = 67, B = 51; inline LL read() { char c = getchar(); LL x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int N, M; struct LinearBasis { #define LL long long LL P[63]; int B; LinearBasis() { B = 62; memset(P, 0, sizeof(P)); } void clear() { memset(P, 0, sizeof(P)); } void insert(LL val) { for(int i = B; i >= 0; i--) { if(!(val >> i & 1)) continue; if(P[i]) {val ^= P[i]; continue;} for(int j = 0; j < i; j++) if(val >> j & 1) val ^= P[j]; for(int j = i + 1; j <= B; j++) if(P[j] >> i & 1) P[j] ^= val; P[i] = val; return ; } } LL QueryMax() { LL ans = 0; for(int i = 0; i <= B; i++) ans ^= P[i]; return ans; } LL QueryKth(LL k) { std::vector<int> v; for(int i = 0; i <= B; i++) if(P[i]) v.push_back(P[i]); if(v.size() != N) k--; if(k > ((1ll << v.size()) - 1)) return -1; LL ans = 0; for(int i = 0; i < v.size(); i++) if(k >> i & 1) ans ^= v[i]; return ans; } #undef LL }Ba; void solve() { N = read(); for(int i = 1; i <= N; i++) Ba.insert(read()); M = read(); while(M--) cout << Ba.QueryKth(read()) << endl; } signed main() { int T = read(); for(int i = 1; i <= T; i++) Ba.clear(), printf("Case #%d:\n", i), solve(); return 0; }
多项式
FFT

// luogu-judger-enable-o2 #include<cstdio> #include<algorithm> #include<cmath> #define Pi acos(-1) using namespace std; const int MAXN = 4 * 1e6 + 10; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int N, M, limit = 1, L; struct complex { double x, y; complex(double xx = 0, double yy = 0) {x = xx, y = yy;} complex operator + (const complex &rhs) { return complex(x + rhs.x, y + rhs.y); } complex operator - (const complex &rhs) { return complex(x - rhs.x, y - rhs.y); } complex operator * (const complex &rhs) { return complex(x * rhs.x - y * rhs.y, x * rhs.y + y * rhs.x); } }a[MAXN], b[MAXN]; int r[MAXN]; void FFT(complex *A, int type) { for(int i = 0; i < limit; i++) if(i < r[i]) swap(A[i], A[r[i]]); for(int mid = 1; mid < limit; mid <<= 1) { complex Wn = complex(cos(Pi / mid), type * sin(Pi / mid)); for(int R = mid << 1, j = 0; j < limit; j += R) { complex w = complex(1, 0); for(int k = 0; k < mid; k++, w = w * Wn) { complex x = A[j + k], y = w * A[j + k +mid]; A[j + k] = x + y, A[j + k + mid] = x - y; } } } } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); #endif N = read(); M = read(); for(int i = 0; i <= N; i++) a[i].x = read(); for(int i = 0; i <= M; i++) b[i].x = read(); while(limit <= N + M) limit <<= 1, L++; for(int i = 0; i <= limit; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) << (L - 1)); FFT(a, 1);FFT(b, 1); for(int i = 0; i < limit; i++) a[i] = a[i] * b[i]; FFT(a, -1); for(int i = 0; i <= N + M; i++) printf("%d ", (int)(a[i].x / limit + 0.5)); return 0; }
NTT

// luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<algorithm> #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1<<21, stdin), p1 == p2) ? EOF : *p1++) #define swap(x,y) (x ^= y, y ^= x, x ^= y) #define mul(a, b) 1ll * a * b % P #define add(a, b) (a + b >= P ? a + b - P : a + b) #define dec(a, b) (a - b < 0 ? a - b + P : a - b) #define rg register using namespace std; const int MAXN = 4 * 1e6, P = 998244353, Gi = 3; char buf[1<<21], *p1 = buf, *p2 = buf; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } char obuf[1<<24], *O=obuf; void print(int x) { if(x > 9) print(x / 10); *O++= x % 10 + '0'; } inline int fastpow(int a, int k) { int base = 1; while(k) { if(k & 1) base = mul(a, base); a = mul(a, a); k >>= 1; } return base % P; } int N, r[MAXN], A[MAXN], B[MAXN], Og[MAXN], F[MAXN], Q[MAXN], G[MAXN], R[MAXN]; inline void NTT(int *A, int type, int len) { int limit = 1, L = 0; while(limit < len) limit <<= 1, L++; for(rg int i = 0; i < limit; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) << (L - 1)); for(rg int i = 0; i < limit; i++) if(i < r[i]) swap(A[i], A[r[i]]); for(rg int mid = 1; mid < limit; mid <<= 1) { int R = mid << 1; int W = fastpow(Gi, (P - 1) / R); Og[0] = 1; for(rg int j = 1; j < mid; j++) Og[j] = mul(Og[j - 1], W); for(rg int j = 0; j < limit; j += R) { for(rg int k = 0; k < mid; k++) { const int x = A[j + k], y = mul(Og[k], A[j + k + mid]); A[j + k] = add(x, y), A[j + k + mid] = dec(x, y); } } } if(type == -1) { std::reverse(&A[1], &A[limit]); for(int i = 0, inv = fastpow(len , P - 2); i < limit; i++) A[i] = 1ll * A[i] * inv % P; } } void Inv(int *a, int *b, int len) {// a要求的多项式 b逆元 len:要求的逆元的长度 if(len == 1) { b[0] = fastpow(a[0], P - 2); return ; } Inv(a, b, len >> 1); for(rg int i = 0; i < len; i++) A[i] = a[i], B[i] = b[i]; NTT(A, 1, len << 1); NTT(B, 1, len << 1); for(rg int i = 0; i < (len << 1); i++) A[i] = mul(mul(A[i], B[i]), B[i]) ; NTT(A, -1, len << 1); for(rg int i = 0; i < len; i++) b[i] = (1ll * (b[i] << 1) % P + P - A[i] ) % P; } void Mul(int *a, int *b, int *c, int N) { int len; for(len = 1; len < N; len <<= 1); NTT(a, 1, len); NTT(b, 1, len); for(int i = 0; i < len; i++) c[i] = 1ll * a[i] * b[i] % P; NTT(c, -1, len); } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #endif int N = read(), M = read(); for(int i = 0; i <= N; i++) F[i] = read(); for(int i = 0; i <= M; i++) G[i] = read(); /*reverse(F, F + N + 1); reverse(G, G + M + 1);*/ Mul(F, G, R, N + M + 1); for(int i = 0; i <= N + M; i++) print(R[i]), *O++ = ' '; fwrite(obuf, O-obuf, 1 , stdout); return 0; }
作者:自为风月马前卒
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。



