P3381 【模板】最小费用最大流

题目描述

如题，给出一个网络图，以及其源点和汇点，每条边已知其最大流量和单位流量费用，求出其网络最大流和在最大流情况下的最小费用。

输入输出格式

输入格式：

 

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含四个正整数ui、vi、wi、fi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi），单位流量的费用为fi。

 

输出格式：

 

一行，包含两个整数，依次为最大流量和在最大流量情况下的最小费用。

 

输入输出样例

输入样例#1：
4 5 4 3
4 2 30 2
4 3 20 3
2 3 20 1
2 1 30 9
1 3 40 5
输出样例#1：
50 280

说明

时空限制：1000ms,128M

（BYX：最后两个点改成了1200ms）

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=1000，M<=1000

对于100%的数据：N<=5000，M<=50000

样例说明：

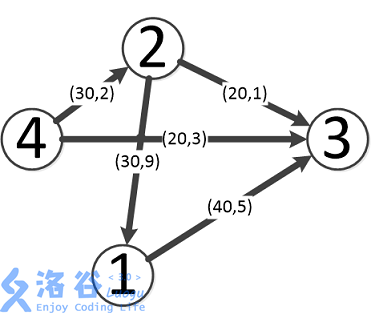
如图，最优方案如下：

第一条流为4-->3，流量为20，费用为3*20=60。

第二条流为4-->2-->3，流量为20，费用为（2+1）*20=60。

第三条流为4-->2-->1-->3，流量为10，费用为（2+9+5）*10=160。

故最大流量为50，在此状况下最小费用为60+60+160=280。

故输出50 280。

 

SPFA费用流的模板题，

用SPFA检查是否可以增广

 

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 #include<cmath>
  5 #include<queue>
  6 using namespace std;
  7 const int MAXN=2000001;
  8 const int maxn=0x7fffffff;
  9 void read(int &n)
 10 {
 11     char c='+';int x=0;bool flag=0;
 12     while(c<'0'||c>'9'){c=getchar();if(c=='-')flag=1;}
 13     while(c>='0'&&c<='9'){x=x*10+(c-48);c=getchar();}
 14     flag==1?n=-x:n=x;
 15 }
 16 struct node
 17 {
 18     int u,v,flow,spend,nxt;
 19 }edge[MAXN];
 20 int head[MAXN];
 21 int num=0;
 22 int n,m,s,t;
 23 int ans=0,maxflow=0;
 24 int dis[MAXN];
 25 int vis[MAXN];
 26 int from[MAXN];
 27 void add_edge(int x,int y,int z,int c)
 28 {
 29     edge[num].u=x;
 30     edge[num].v=y;
 31     edge[num].flow=z;
 32     edge[num].spend=c;
 33     edge[num].nxt=head[x];
 34     head[x]=num++;
 35 }
 36 bool SPFA()
 37 {
 38     for(int i=1;i<=n;i++)
 39         dis[i]=maxn;
 40     memset(vis,0,sizeof(vis));
 41     dis[s]=0;
 42     queue<int>q;
 43     q.push(s);
 44     vis[s]=1;
 45     while(q.size()!=0)
 46     {
 47         int p=q.front();
 48         q.pop();
 49         vis[p]=0;
 50         for(int i=head[p];i!=-1;i=edge[i].nxt)
 51         {
 52             if(dis[edge[i].v]>dis[edge[i].u]+edge[i].spend&&edge[i].flow>0)
 53             {
 54                 dis[edge[i].v]=dis[edge[i].u]+edge[i].spend;
 55                 from[edge[i].v]=i;
 56                 if(!vis[edge[i].v])
 57                 {
 58                     vis[edge[i].v]=1;
 59                     q.push(edge[i].v);
 60                 }
 61             }
 62         }
 63     }
 64     if(dis[t]!=maxn)
 65         return 1;
 66     else 
 67         return 0;
 68     
 69 }
 70 void f()
 71 {
 72     int mn=maxn;
 73     for(int i=t;i!=s;i=edge[from[i]].u)
 74         mn=min(mn,edge[from[i]].flow);
 75     for(int i=t;i!=s;i=edge[from[i]].u)
 76     {
 77         edge[from[i]].flow-=mn;
 78         edge[from[i]^1].flow+=mn;
 79         ans+=(mn*edge[from[i]].spend);
 80     }
 81     maxflow+=mn;
 82 }
 83 int main()
 84 {
 85     read(n);read(m);read(s);read(t);
 86     //s=1;
 87     //t=n;
 88     memset(head,-1,sizeof(head));
 89     for(int i=1;i<=m;i++)
 90     {
 91         int x,y,z,c;
 92         read(x);read(y);read(z);read(c);
 93         add_edge(x,y,z,c);
 94         add_edge(y,x,0,-c);
 95     }
 96     while(SPFA())
 97         f();
 98     printf("%d %d",maxflow,ans);
 99     return 0;
100 }

 

posted @ 2017-07-28 20:30  自为风月马前卒  阅读(403)  评论(2)  编辑  收藏  举报

Contact with me