P3382 【模板】三分法

题目描述

如题，给出一个N次函数，保证在范围[l,r]内存在一点x，使得[l,x]上单调增，[x,r]上单调减。试求出x的值。

输入输出格式

输入格式：

 

第一行一次包含一个正整数N和两个实数l、r，含义如题目描述所示。

第二行包含N+1个实数，从高到低依次表示该N次函数各项的系数。

 

输出格式：

 

输出为一行，包含一个实数，即为x的值。四舍五入保留5位小数。

 

输入输出样例

输入样例#1：

3 -0.9981 0.5
1 -3 -3 1

输出样例#1：

-0.41421

说明

时空限制：50ms,128M

数据规模：

对于100%的数据：7<=N<=13

样例说明：

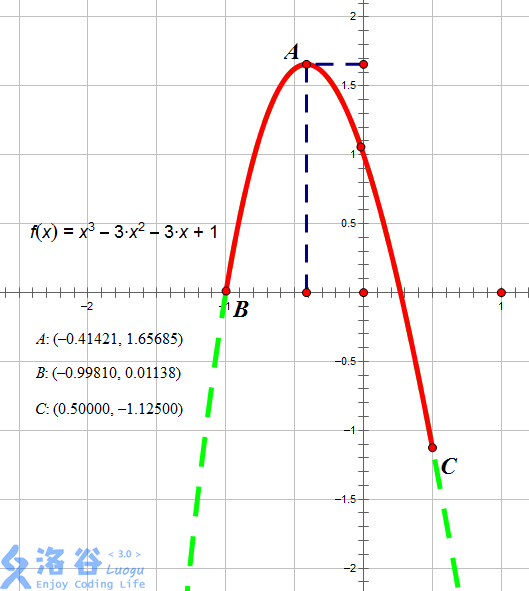
如图所示，红色段即为该函数f(x)=x^3-3x^2-3x+1在区间[-0.9981,0.5]上的图像。

当x=-0.41421时图像位于最高点，故此时函数在[l,x]上单调增，[x,r]上单调减，故x=-0.41421，输出-0.41421。

 

在[L, R]中，

取a = (2L + R) / 3, b = (L + 2R) / 3。

如果f(a) > f(b)

则答案在[L, b]里（如果在[b, R]里，则[a, b]段递增），

如果f(a) < f(b)

则答案在[a, R]里（如果在[L, a]里，则[a, b]段递减），

递归或循环即可。

复杂度是log(2/3, 1e-5/d)=log(3/2, d*100000)≈30 + 1.7lgd.

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
#include<algorithm>
#define lli long long int 
using namespace std;
const int MAXN=21;
void read(int &n)
{
    char c='+';int x=0;bool flag=0;
    while(c<'0'||c>'9')
    {c=getchar();if(c=='-')flag=1;}
    while(c>='0'&&c<='9')
    {x=(x<<1)+(x<<3)+c-48;c=getchar();}
    flag==1?n=-x:n=x;
}
double n,l,r;
double xi[MAXN];
double nowl,nowr;
double f(double x)
{
    double ans=0;
    for(int i=1;i<=n;i++)
    {
        double tmp=xi[i];
        for(int j=1;j<=n-i+1;j++)
        {
            tmp=tmp*x;
        }
        ans+=tmp;
    }
    return ans;
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>l>>r;
    for(int i=1;i<=n;i++)
        cin>>xi[i];
    nowl=l;
    nowr=r;
    while(fabs(nowl-nowr)>0.000001)
    {
        double wl=nowl+(nowr-nowl)/3;
        double wr=nowl+(nowr-nowl)/3*2;
        if(f(wl)>f(wr))
            nowr=wr;
        else 
            nowl=wl;
    }
    printf("%.5f",nowl);
    return 0;
}