量化投资学习笔记22——回归分析:支持向量机
因为新冠肺炎疫情,诊所还没复工。这是在家用手机敲的,代码显示有问题。等复工以后在电脑上改,各位先凑和看吧。
支持向量机(Support Vector Machine, SVM)是一种基于统计学习的模式识别的分类方法,主要用于模式识别。所谓支持向量指的是在分割区域边缘的训练样本点,机是指算法。就是要找到具有最大间隔的分隔面。实际上解决的是一个最优分类器设计的问题。
问题
目的:找到一个最优分类器,即找到一个分类器,使得分类间隔最大。
优化的目标函数:分类间隔,需要使得分类间隔最大。
优化对象:分类超平面(决策平面),通过调整分类超平面的位置,使得间隔最大,实现优化目标。

超平面(Hyperplane),指n维欧氏空间中余维度等于1的线性子空间。二维空间中为一条直线,三维空间中为一个二维平面。
间隔:支持向量对应点到分类超平面的垂直距离的两倍。即W =2d。
现在要做的是,在所有的样本点中,找到合适的支持向量,在保证分类正确的前提下,让间隔W = 2d最大。
再往后就是具体的求解推导的过程了,听听就行了。
对于线性不可分的情况,考虑将样本映射到更高维的空间中去,希望在这个高维空间中其线性可分。
例:一条直线上的两个不同分类的点也许不可分,将其映射到二维平面里也许就可以区分了。

如果原始空间是有限维,即属性数有限,一定存在一个高维特征空间使样本线性可分。
这就引出了核函数的概念。K(x, x') = φ(x)·φ(x')
当后者不容易求时,可找到一个函数K,即为核函数。
推导看不懂。
选择核函数无明确的指导原则,常用RBF,其次是线性核。
异常点造成的非线性,SVM允许在一定程度上偏离一下超平面。
SVM多分类
直接法:将多分类面的参数求解合并到一个最优化问题中。
间接法:组合多个二分类SVM分类器
有一对一法和一对多法。
下面来实践,还是使用iris数据。参考https://blog.csdn.net/u012679707/article/details/80501358
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn import svm
# 转换类别
def Iris_label(s):
it = {b'Iris-setosa':0, b'Iris-versicolor':1, b'Iris-virginica':2}
return it[s]
if __name__ == "__main__":
# 读取数据
data = np.loadtxt("iris.data", dtype = float, delimiter = ',', converters = {4 : Iris_label})
print(data)
# 划分数据与标签
x, y = np.split(data, indices_or_sections = (4,), axis = 1)
# 为了绘图,只选前两页
x = x[:, 0:2]
train_data, test_data, train_label, test_label = train_test_split(x, y, random_state = 1, train_size = 0.6, test_size = 0.4)
print("训练集大小:", train_data.shape)
print(train_data)
print(test_data)
# 训练svm分类器
classifier = svm.SVC(C = 2, kernel = "rbf", gamma = 10, decision_function_shape = "ovr") #ovr 一对多策略
classifier.fit(train_data, train_label.ravel())
# 计算分类准确率
print("训练集:", classifier.score(train_data, train_label))
print("测试集:", classifier.score(test_data, test_label))
# 查看决策函数
print("训练决策函数:", classifier.decision_function(train_data))
print("预测结果:", classifier.predict(train_data))
结果:
训练集: 0.8555555555555555
测试集: 0.7
训练集比测试集结果好。
再画图看看。
# 绘图
fig = plt.figure()
x1_min, x1_max = x[:, 0].min(), x[:, 0].max()
x2_min, x2_max = x[:, 1].min(), x[:, 1].max()
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]
grid_test = np.stack((x1.flat, x2.flat), axis = 1)
# 设置颜色
cm_light = ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = ListedColormap(['g','r','b'])
grid_hat = classifier.predict(grid_test)
grid_hat = grid_hat.reshape(x1.shape)
# 绘图
plt.pcolormesh(x1, x2, grid_hat, cmap = cm_light)
plt.scatter(x[:, 0], x[:, 1], c = y[:, 0], s = 30, cmap = cm_dark)
plt.scatter(test_data[:, 0], test_data[:, 1], c = test_label[:, 0], s = 30, edgecolors = "k", zorder = 2, cmap = cm_dark)
plt.xlabel("length")
plt.ylabel("width")
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.savefig("result.png")
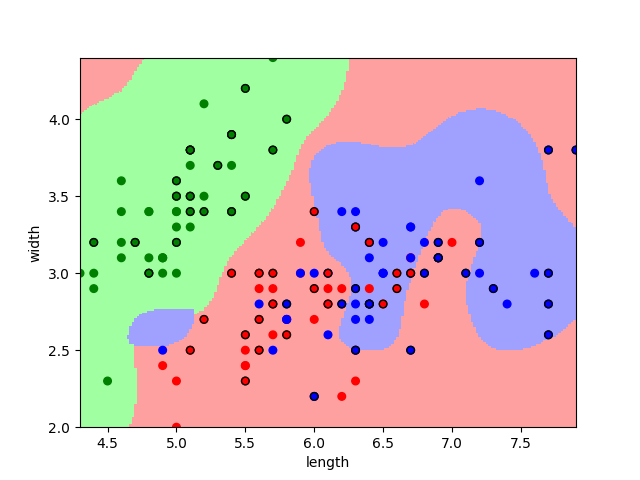
试一下把四列数据都进行建模的结果:
四列数据都进行建模的结果
训练集: 1.0
测试集: 0.95
结果很好。
接下来用这个方法解决一下泰坦尼克号问题吧。下次。
本文代码:
https://github.com/zwdnet/MyQuant/tree/master/21
我发文章的四个地方,欢迎大家在朋友圈等地方分享,欢迎点“在看”。
我的个人博客地址:https://zwdnet.github.io
我的知乎文章地址: https://www.zhihu.com/people/zhao-you-min/posts
我的博客园博客地址: https://www.cnblogs.com/zwdnet/
我的微信个人订阅号:赵瑜敏的口腔医学学习园地





