量化投资学习笔记19——回归分析:实操,泰坦尼克号乘客生还机会预测,线性回归方法。
用kaggle上的泰坦尼克的数据来实操。
https://www.kaggle.com/c/titanic/overview
在主页上下载了数据。
任务:使用泰坦尼克号乘客数据建立机器学习模型,来预测乘客在海难中是否生存。
在实际海难中,2224位乘客中有1502位遇难了。似乎有的乘客比其它乘客更有机会获救。本任务的目的就是找出哪类人更容易获救。
数据集有两个,一个是训练数据集"train.csv",另一个是测试数据集"test.csv"。
官方推荐一个教程:https://www.kaggle.com/alexisbcook/titanic-tutorial
先照着来吧。
就是熟悉了整个结果上传流程,使用了随机树森林算法,结果正确率是77.551%,排9444位。
接下来就是我自己折腾了。
读取数据后,用info函数看看。
print(train_data.info())
print(test_data.info())
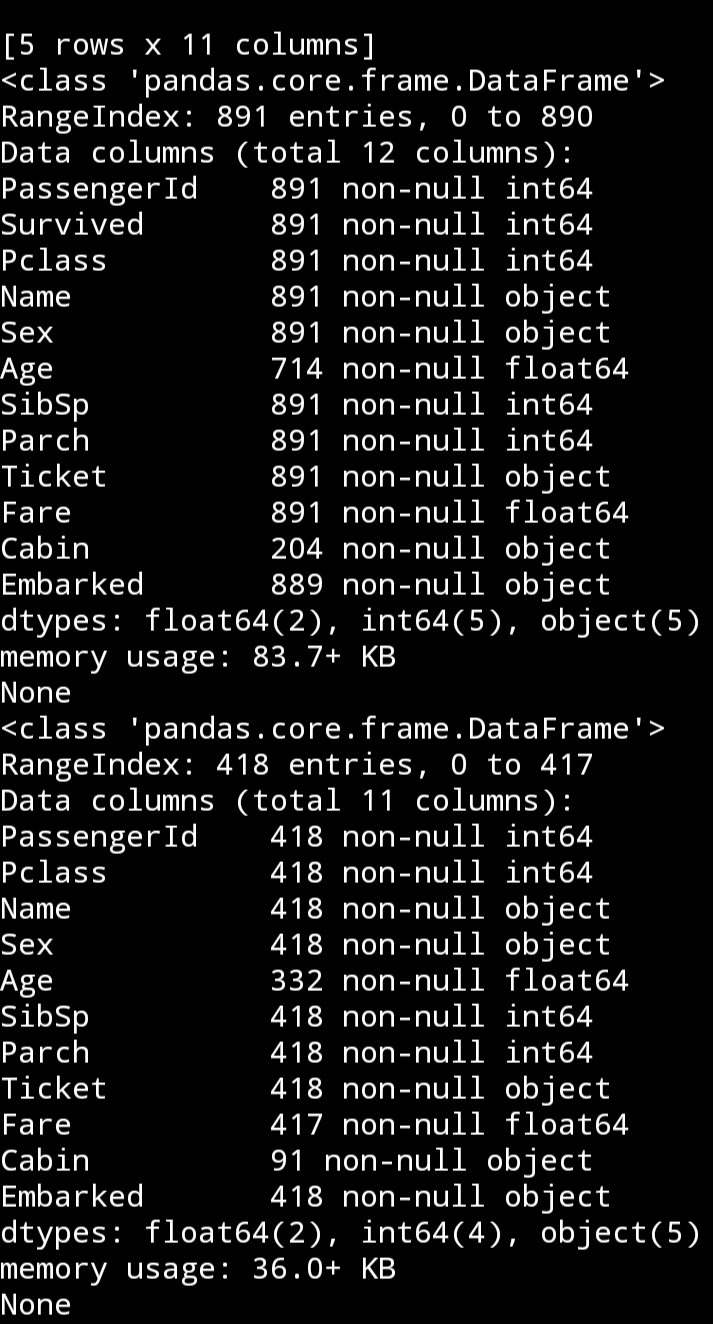
有三列数据有缺失值。先将数据可视化吧。

第一张是遇难者与获救者的比例,第二张是三个票价等级的人数,第三张是遇难者及获救者的年龄分布,第四张是按船票等级的年龄分布,最后一张是三个港口的登船人数。
再画一个不同船票等级的乘客的获救率。
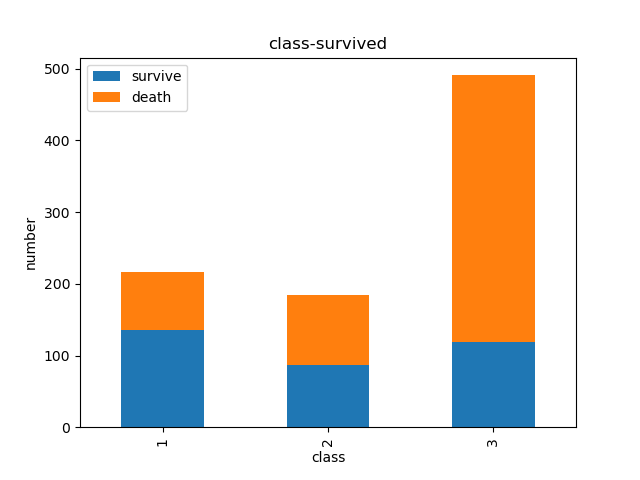
可见高等级的获救率更高。
再画图看性别与获救的关系

真是lady first
下面再看各个舱别的获救人数。

高等舱的女性生还率最高,其次是高等舱男性,低等舱男性生还率最低。
再看各港口登船的情况。

三个港口登船人数依次下降,死亡率差不多。
有堂兄弟妹,有子女父母对死亡率的影响。
g = train_data.groupby(["SibSp", "Survived"])
df = pd.DataFrame(g.count()["PassengerId"])
print(df)
g = train_data.groupby(["Parch", "Survived"])
df = pd.DataFrame(g.count()["PassengerId"])
print(df)

没看出啥来。
Cabin缺失数据太多,画图看看数据缺失的和有数据的两组死亡率是否有差别。
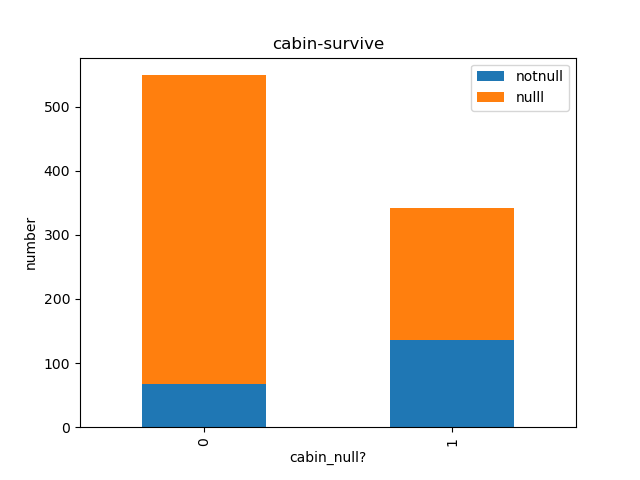
貌似有cabin记录的获救率高一些。
接下来就要清洗数据了,主要是处理缺失的数据,进行数据转换。
(下面参考了https://blog.csdn.net/weixin_44451032/article/details/100103998)
先查看缺失值
print(train_data.isnull().sum())
print(test_data.isnull().sum())

主要是Age、Embarked和Cabin三个字段的缺失数据较多。
Age用年龄中位数填充,登船地点填充为众数,Cabin则采用因子化,即根据有无Cabin数据分为两类。
train_data["Age"].fillna(train_data["Age"].median(), inplace = True)
test_data["Age"].fillna(test_data["Age"].median(), inplace = True)
train_data["Embarked"] = train_data["Embarked"].fillna('S')
train_data.loc[(train_data.Cabin.notnull()), "Cabin"] = 1
train_data.loc[(train_data.Cabin.isnull()), "Cabin"] = 0
test_data.loc[(test_data.Cabin.notnull()), "Cabin"] = 1
test_data.loc[(test_data.Cabin.isnull()), "Cabin"] = 0
再看看有没有缺失数据的

行啦。
接下来把非数值数据转换为数值数据
将性别数据转换为数值数据
train_data.loc[train_data["Sex"] == "male", "Sex"] = 0
train_data.loc[train_data["Sex"] == "female", "Sex"] = 1
test_data.loc[test_data["Sex"] == "male", "Sex"] = 0
test_data.loc[test_data["Sex"] == "female", "Sex"] = 1
将登船地点数据转换为数值数据
C:0, Q:1, S:2
train_data.loc[train_data["Embarked"] == 'C', "Embarked"] = 0
train_data.loc[train_data["Embarked"] == 'Q', "Embarked"] = 1
train_data.loc[train_data["Embarked"] == 'S', "Embarked"] = 2
test_data.loc[test_data["Embarked"] == 'C', "Embarked"] = 0
test_data.loc[test_data["Embarked"] == 'Q', "Embarked"] = 1
test_data.loc[test_data["Embarked"] == 'S', "Embarked"] = 2
print(train_data.head())
print(test_data.head())
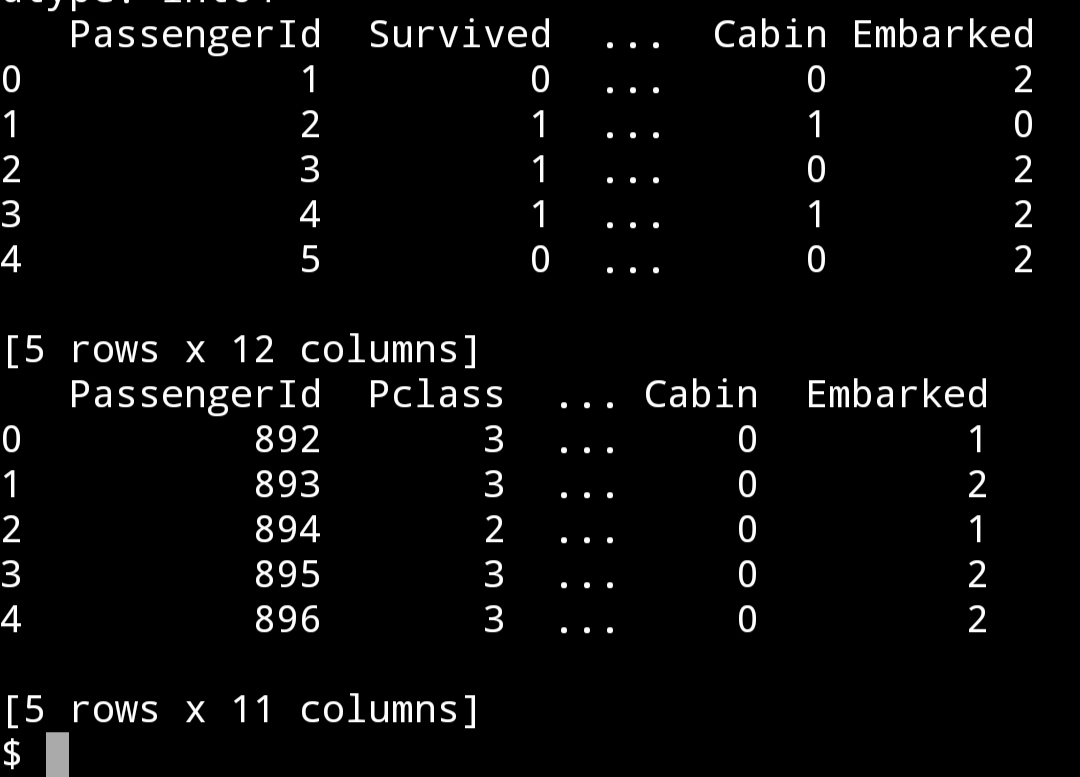
最后,提取我们认为在预测模型中重要的特征: Pclass,Sex,Age,Embarked,SibSp,Parch,Cabin
构建一个新的数据表。
columns = ['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Embarked', 'Survived', 'Cabin']
new_train_data = train_data[columns]
print(new_train_data.info())

OK,可以开始建模了。
先用刚学的线性回归模型。
线性回归模型
特征变量
predictors = ['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Embarked', 'Cabin']
LR = LinearRegression()
设置进行交叉验证
kf = KFold(5, random_state = 0)
train_target = new_train_data["Survived"]
accuracys = []
for train, test in kf.split(new_train_data):
LR.fit(new_train_data.loc[train, predictors], new_train_data.loc[train, "Survived"])
pred = LR.predict(new_train_data.loc[test, predictors])
pred[pred >= 0.6] = 1
pred[pred < 0.6] = 0
accuracy = len(pred[pred == new_train_data.loc[test, "Survived"]])/len(test)
accuracys.append(accuracy)
print(np.mean(accuracys))
结果:0.799083547799887
提交kaggle以后结果并不好。

再看看回归的具体结果。
print("回归系数:", LR.coef_)
print("截距:", LR.intercept_)
X = new_train_data[predictors]
y = new_train_data["Survived"]
Y = LR.predict(X)
print("模型评分:", LR.score(X, y))
i = 241
for index in predictors:
X = new_train_data[index]
fig = plt.subplot(i)
i += 1
plt.plot(X, Y, "*")
plt.plot(X, y, "o")
plt.savefig("LRtest.png")
结果:
回归系数: [-0.13393963 0.50834201 -0.00505791 -0.03254537 -0.03019912 -0.02651349
0.11037934]
截距: 0.7106465692231267
0.40082362319192455
模型的R²才0.4(越接近1越理想)。

看着也没啥联系。再看看每个回归系数的检验吧。sklearn里似乎没有相关函数,还是用statsmodels模块里的函数。
# 看模型的假设检验
X = new_train_data[predictors]
X = sm.add_constant(X)
model = sm.OLS(Y, X).fit()
res = get_index(model)
print("回归参数", model.params)
print("回归结果", res)
print(model.summary())

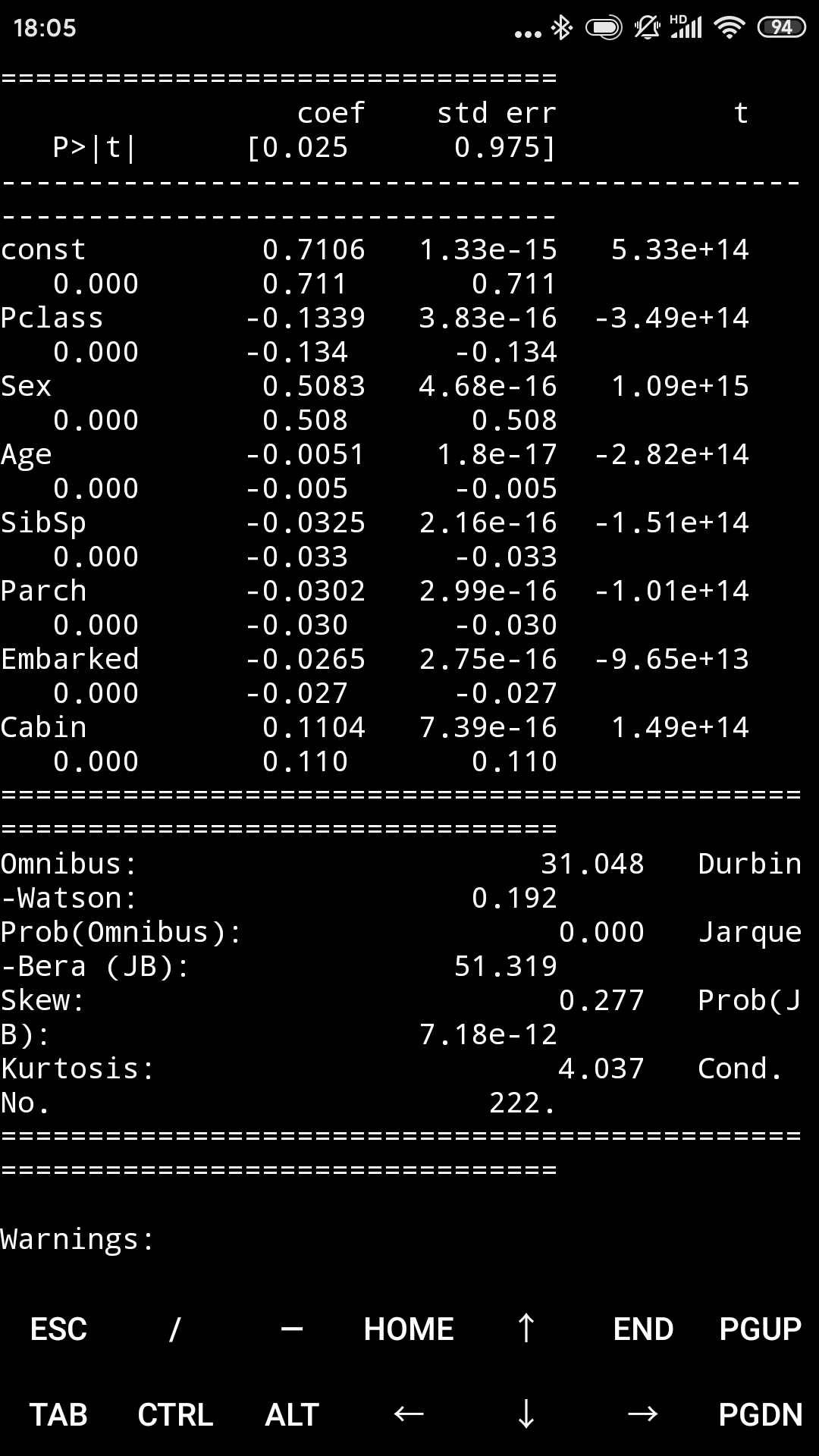
回归系数跟用sklearn算的一样,但检验结果却特别好,有点诡异。可能是因为这个问题很多变量只有少数几个值,甚至两个值,是离散变量,不适合直接用线性回归。
再试试其它方法。
本文代码: https://github.com/zwdnet/MyQuant/tree/master/titanic
以后关于这个问题的代码都放到这里面。
我发文章的四个地方,欢迎大家在朋友圈等地方分享,欢迎点“在看”。
我的个人博客地址:https://zwdnet.github.io
我的知乎文章地址: https://www.zhihu.com/people/zhao-you-min/posts
我的博客园博客地址: https://www.cnblogs.com/zwdnet/
我的微信个人订阅号:赵瑜敏的口腔医学学习园地



 浙公网安备 33010602011771号
浙公网安备 33010602011771号