量化投资学习笔记18——回归分析:变量的选择、多重共线性及回归分析的改进

如果模型包含了所有影响因素，称为全模型。如果只包含部分影响因素，称为选模型。
影响:①未选入的参数不全为0时，选模型的回归参数为有偏估计。②选模型的预测结果是有偏预测。③选模型的参数估计有较小的方差。④选模型的预测残差有较小的方差。⑤选模型预测的均方误差比全模型小。
自变量选择的准则:
①残差平方和SSE越小，决定系数R²越大越好。并非如此。
②自由度调整复决定系数达到最大。
③赤池信息量(Akaike Information Criterion, AIC)达到最小:基于最大似然估计原理。
④统计量Cp达到最小。
下面用课程里的一个数据集进行实操，有三个可选自变量，分别计算各种自变量选择组合的R²，adjR²，AIC，Cp。
其中前三个指标都能直接用statsmodels获得，而Cp没找到如何获得，就算前三个吧。

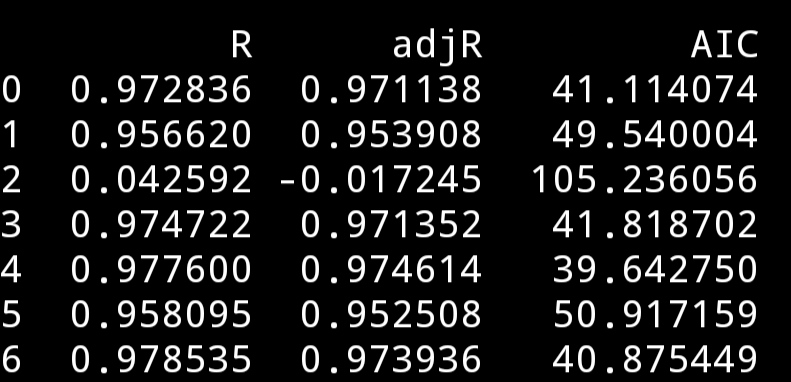
最后几个都很好。
自变量选择的方法
前进法:变量由少到多，逐个加入，直到没有可引入的变量。
步骤:
①对所有m个自变量分别进行一元线性回归。②对回归方程计算F统计量，找出最大的一个。
③若其大于预先指定的检验水平，该变量入选。
④将该变量与剩余的m-1个变量组合，分别进行建模，按照上面的过程选出F值最大的一个，如果大于检验水平，入选。
⑤重复上述步骤，直到没有满足条件的变量为止。

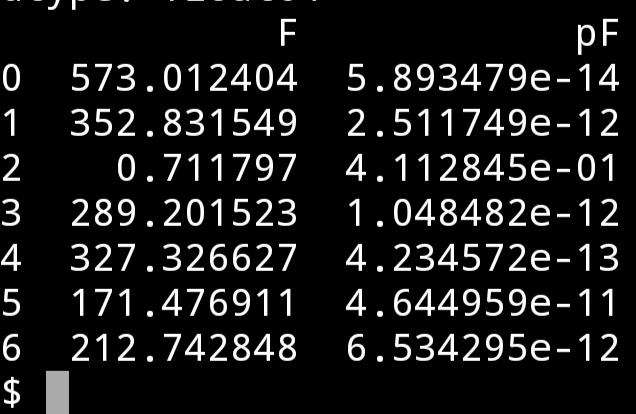
看实测的结果，除了第三个，即x3的方程，其余都远小于0.05。
前三个是单变量一元线性回归的，x1的方程的F值最大，入选。
然后看x1,x2和x1,x3的回归方程的F值。分别是上面的3，4行。x3入选。
最后看x2入选以后得F值，p仍小于0.05，也入选。因此三个变量均入选。
后退法:变量由多到少，逐个减少，直至没有可以减少的变量。
方法，先对所有变量进行回归，然后看每个回归系数的F值，找到最小的，若小于检验阈值，将该变量去除。直至无法再去除。
两种方法都有各自的优缺点。
逐步回归法:有进有出。一旦入选变量发生变化就对所有变量进行F检验。
多重共线性:模型的解释变量之间存在精确或高度相关关系使模型估计失真或难以估计准确。
原因:多个自变量存在相同的趋势。②引入了滞后的变量。③样本资料的限制。
影响:参数估计失效;显著性检验失效;模型无应用价值。
诊断:
直观判断:增加或剔除一个自变量，观察模型，如果系数估计值变化很大，说明存在严重的多重共线性。重要的自变量显著性检验没有通过。一些自变量系数正负号与定性分析结果相反。自变量相关系数矩阵中相关系数较大。重要变量的回归系数标准误差较大。
方差扩大因子法。
特征根判定法。
消除方法:
①删除不重要的解释变量
②增大样本量
③回归系数有偏估计
改进的回归方法:岭回归(脊回归)、LASSO回归
回归分析就完了，接下来找个实际的数据集来实操一把吧。
本文代码: https://github.com/zwdnet/MyQuant/tree/master/17

我发文章的四个地方，欢迎大家在朋友圈等地方分享，欢迎点“在看”。
我的个人博客地址：https://zwdnet.github.io
我的知乎文章地址： https://www.zhihu.com/people/zhao-you-min/posts
我的博客园博客地址： https://www.cnblogs.com/zwdnet/
我的微信个人订阅号：赵瑜敏的口腔医学学习园地