Pearson's correlation coefficient when applied to a population is commonly represented by the Greek letter ρ (rho) and may be referred to as the population correlation coefficient or the population Pearson correlation coefficient. The formula for ρ is:
where,  is the covariance,
is the covariance, 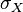 is the standard deviation of
is the standard deviation of 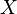 ,
, 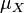 is the mean of
is the mean of 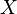 , and
, and 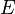 is the expectation.
is the expectation.
Alternative formulae for the sample Pearson correlation coefficient are also available:
The above formula suggests a convenient single-pass algorithm for calculating sample correlations, but, depending on the numbers involved, it can sometimes benumerically unstable.
Spearman's rank correlation coefficient
For a sample of size n, the n raw scores 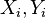 are converted to ranks
are converted to ranks 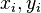 , and ρ is computed from:
, and ρ is computed from:
where 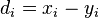 , is the difference between ranks
, is the difference between ranks
示例[编辑]
在此例中,我们要使用下表所给出的原始数据计算一个人的 智商和其每周花在 电视上的小时数的相关性。
智商, 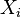 | 每周花在电视上的小时数, 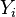 |
| 106 | 7 |
| 86 | 0 |
| 100 | 27 |
| 101 | 50 |
| 99 | 28 |
| 103 | 29 |
| 97 | 20 |
| 113 | 12 |
| 112 | 6 |
| 110 | 17 |
首先,我们必须根据以下步骤计算出 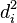 ,如下表所示。
,如下表所示。
- 排列第一列数据 (
![X_i]() )。 创建新列
)。 创建新列 ![x_i]() 并赋以等级值 1,2,3,...n。
并赋以等级值 1,2,3,...n。 - 然后,排列第二列数据 (
![Y_i]() ). 创建第四列
). 创建第四列 ![y_i]() 并相似地赋以等级值 1,2,3,...n。
并相似地赋以等级值 1,2,3,...n。 - 创建第五列
![d_i]() 保存两个等级列的差值 (
保存两个等级列的差值 (![x_i]() 和
和 ![y_i]() ).
). - 创建最后一列
![d^2_i]() 保存
保存 ![d_i]() 的平方.
的平方.
智商, 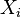 | 每周花在电视上的小时数, 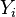 | 等级 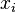 | 等级 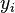 | 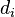 | 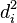 |
| 86 | 0 | 1 | 1 | 0 | 0 |
| 97 | 20 | 2 | 6 | −4 | 16 |
| 99 | 28 | 3 | 8 | −5 | 25 |
| 100 | 27 | 4 | 7 | −3 | 9 |
| 101 | 50 | 5 | 10 | −5 | 25 |
| 103 | 29 | 6 | 9 | −3 | 9 |
| 106 | 7 | 7 | 3 | 4 | 16 |
| 110 | 17 | 8 | 5 | 3 | 9 |
| 112 | 6 | 9 | 2 | 7 | 49 |
| 113 | 12 | 10 | 4 | 6 | 36 |
根据 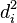 计算
计算 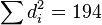 。 样本容量n为 10。 将这些值带入方程
。 样本容量n为 10。 将这些值带入方程
得 ρ = −0.175757575...


![\rho_{X,Y}={\mathrm{cov}(X,Y) \over \sigma_X \sigma_Y} ={E[(X-\mu_X)(Y-\mu_Y)] \over \sigma_X\sigma_Y}](http://images0.cnblogs.com/blog/614747/201502/030033198909678.png)
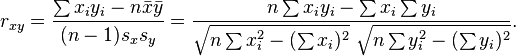
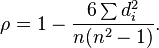
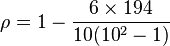

 浙公网安备 33010602011771号
浙公网安备 33010602011771号