二叉树

结点是数据结构中的基础，是构成复杂数据结构的基本组成单位

二叉树：
二叉树是N个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个跟结点和两颗互不相交的，分别称为根结点的左子树和右子树组成

特点：

1）每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点
2）左子树和右子树是有顺序的，次序不能任意颠倒
3）即使树中某结点只有一颗子树，也要区分是左子树还是右子树

性质：

1）在二叉树中的第i层上最多有2i-1 个节点 。（i>=1）
2）二叉树中如果深度为k，那么最多有2k-1个节点。(k>=1）
3）在完去二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。

满二叉树：
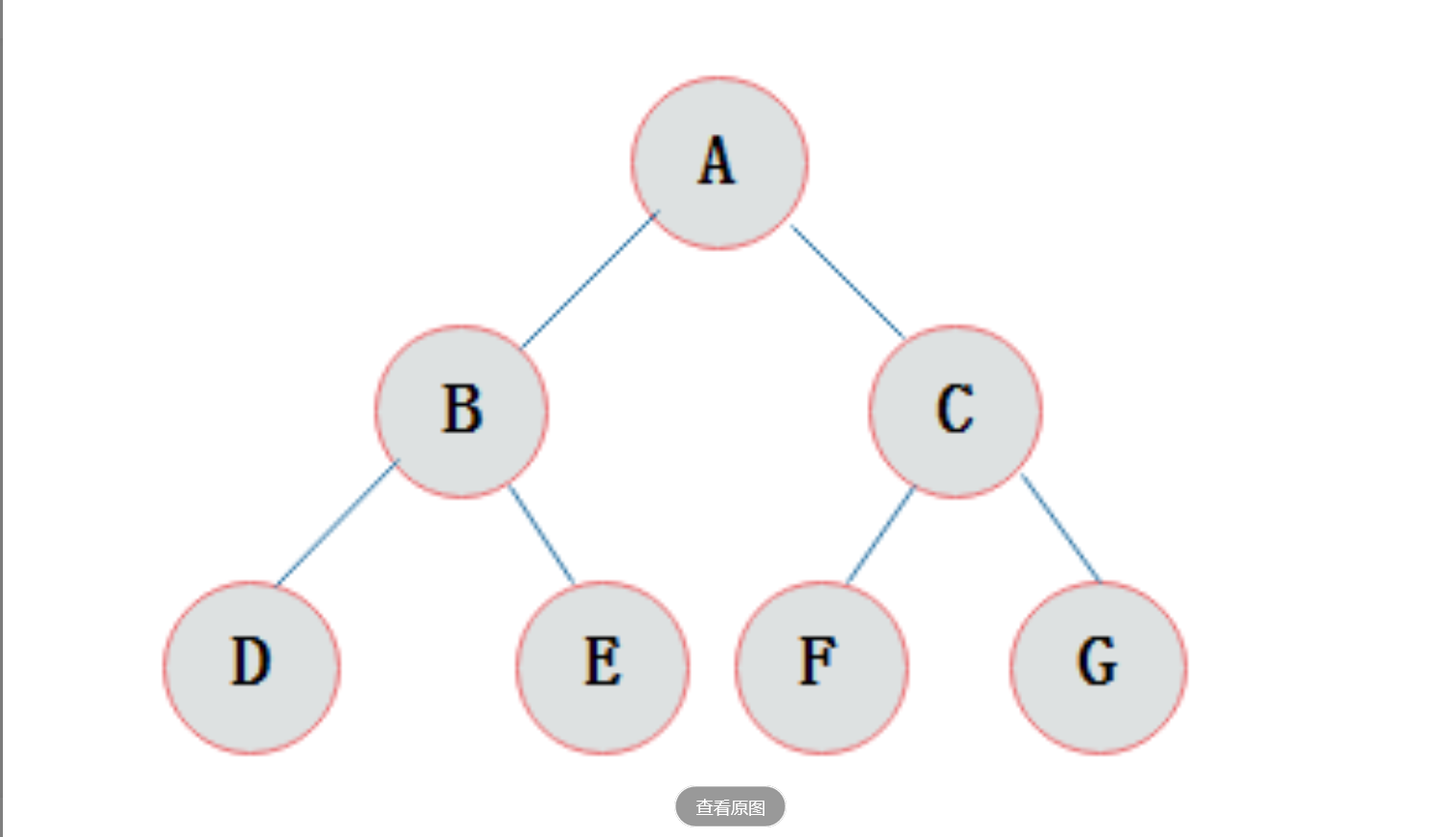
在一颗二叉树中。如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树

特点：

1）叶子只能出现在最下一层，出现在其他层就不可能达到平衡
2）非叶子结点的度一定是2
3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多

完全二叉树：
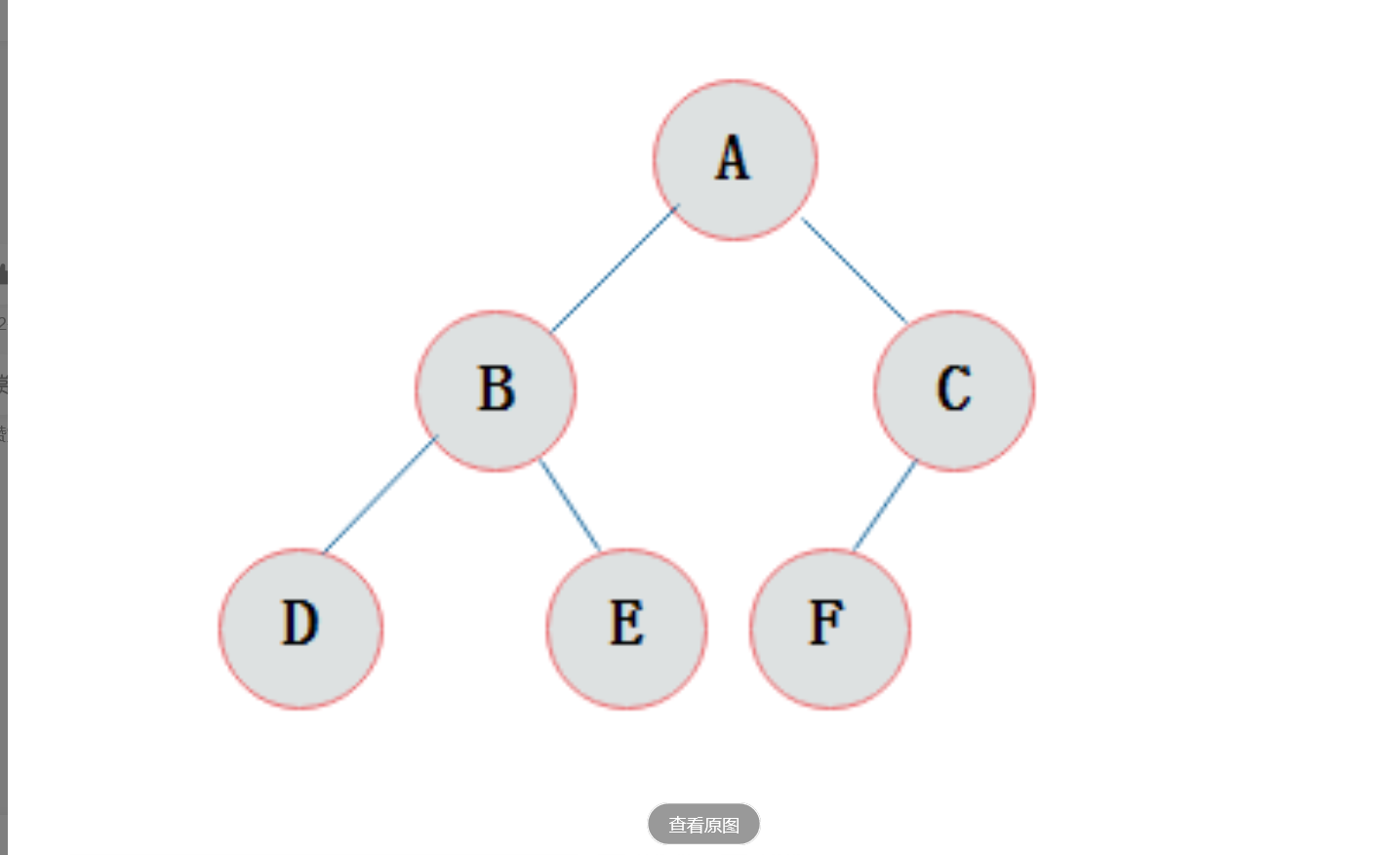
对一颗具有n个结点的二叉树按层编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这颗二叉树称为完全二叉树

特点：

1）叶子结点只能出现在最下层和次下层
2）最下层的叶子结点集中在数的左部
3）倒数第二层若存在叶子结点，一定在右部连续的位置
4）如果结点度为1，则该结点只有左孩子，没有右子树
5）同样结点数目为的二叉树，完全二叉树深度最小
**注：满二叉树一定是完全二叉树，反之不一定成立**

完全二叉树和满二叉树的区别：
完全二叉树，除最后一层可能不满以外，其他各层都达到该层节点的最大数，最后一层如果不满，该层所有节点都全部靠左排
满二叉树，所有层的节点数都达到最大

二叉树的存储结构：顺序存储
二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点，并且结点的存储位置，就是数组的下标索引。

二叉链表：
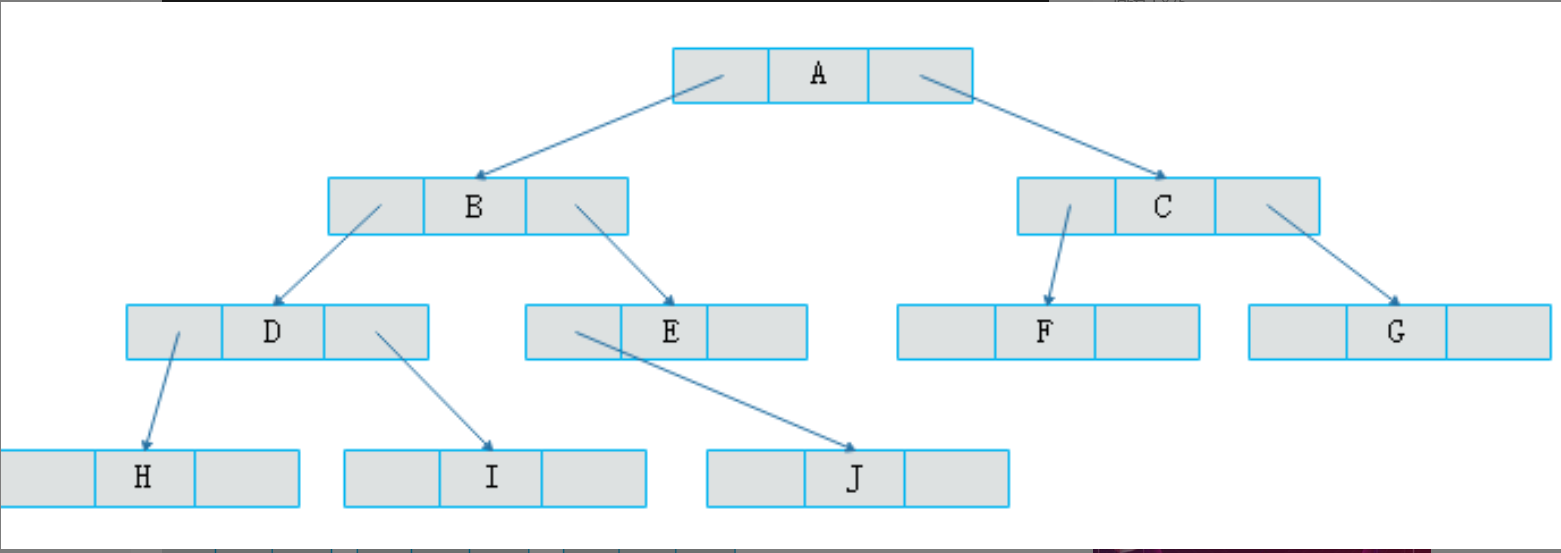
既然顺序存储不能满足二叉树的存储需求，那么考虑采用链式存储。由二叉树定义可知，二叉树的每个结点最多有两个孩子。因此，可以将结点数据结构定义为一个数据和两个指针域。表示方式如图所示：

定义结点代码：

typedef struct BiTNode{
TElemType data;//数据
struct BiTNode *lchild, *rchild;//左右孩子指针
} BiTNode, *BiTree;

二叉树遍历：
二叉树的遍历是指从二叉树的根结点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次，且仅被访问一次。
二叉树的访问次序可以分为四种：

前序遍历
中序遍历
后序遍历
层序遍历

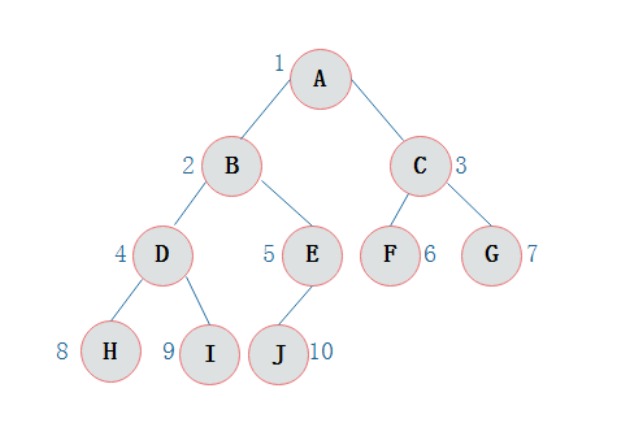
前序遍历：
通俗的说就是从二叉树的根结点出发，当第一次到达结点时就输出结点数据，按照先向左在向右的方向访问。

从根结点出发，则第一次到达结点A，故输出A;
继续向左访问，第一次访问结点B，故输出B；
按照同样规则，输出D，输出H；
当到达叶子结点H，返回到D，此时已经是第二次到达D，故不在输出D，进而向D右子树访问，D右子树不为空，则访问至I，第一次到达I，则输出I；
I为叶子结点，则返回到D，D左右子树已经访问完毕，则返回到B，进而到B右子树，第一次到达E，故输出E；
向E左子树，故输出J；
按照同样的访问规则，继续输出C、F、G；
则所示二叉树的前序遍历输出为：    ABDHIEJCFG

中序遍历：
就是从二叉树的根结点出发，当第二次到达结点时就输出结点数据，按照先向左在向右的方向访问。

从根结点出发，则第一次到达结点A，不输出A，继续向左访问，第一次访问结点B，不输出B；继续到达D，H；
到达H，H左子树为空，则返回到H，此时第二次访问H，故输出H；
H右子树为空，则返回至D，此时第二次到达D，故输出D；
由D返回至B，第二次到达B，故输出B；
按照同样规则继续访问，输出J、E、A、F、C、G；
中序遍历输出为：    HDIBJEAFCG

后序遍历：
就是从二叉树的根结点出发，当第三次到达结点时就输出结点数据，按照先向左在向右的方向访问。

从根结点出发，则第一次到达结点A，不输出A，继续向左访问，第一次访问结点B，不输出B；继续到达D，H；
到达H，H左子树为空，则返回到H，此时第二次访问H，不输出H；
H右子树为空，则返回至H，此时第三次到达H，故输出H；
由H返回至D，第二次到达D，不输出D；
继续访问至I，I左右子树均为空，故第三次访问I时，输出I；
返回至D，此时第三次到达D，故输出D；
按照同样规则继续访问，输出J、E、B、F、G、C，A；
后序遍历输出为：    HIDJEBFGCA

虽然二叉树的遍历过程看似繁琐，但是由于二叉树是一种递归定义的结构，故采用递归方式遍历二叉树的代码十分简单。
递归实现代码如下：

/*二叉树的前序遍历递归算法*/
void PreOrderTraverse(BiTree T)
{
    if(T==NULL)
    return;
    printf("%c", T->data);  /*显示结点数据，可以更改为其他对结点操作*/
    PreOrderTraverse(T->lchild);    /*再先序遍历左子树*/
    PreOrderTraverse(T->rchild);    /*最后先序遍历右子树*/
}


/*二叉树的中序遍历递归算法*/
void InOrderTraverse(BiTree T)
{
    if(T==NULL)
    return;
    InOrderTraverse(T->lchild); /*中序遍历左子树*/
    printf("%c", T->data);  /*显示结点数据，可以更改为其他对结点操作*/
    InOrderTraverse(T->rchild); /*最后中序遍历右子树*/
}


/*二叉树的后序遍历递归算法*/
void PostOrderTraverse(BiTree T)
{
    if(T==NULL)
    return;
    PostOrderTraverse(T->lchild);   /*先后序遍历左子树*/
    PostOrderTraverse(T->rchild);   /*再后续遍历右子树*/
    printf("%c", T->data);  /*显示结点数据，可以更改为其他对结点操作*/
}

层次遍历：
就是按照树的层次自上而下的遍历二叉树。针对图所示二叉树的层次遍历结果为：ABCDEFGHIJ