GDOI-2022 题解

D1T1 预处理器

我们先用 unordered_map 将字符串编号

然后 #define 的时候就加边，#undef 的时候就删边，然后询问的时候直接递归就行了：如果没有编号的，或者是编号了但没有出边的，又或者是指向的字符串已经展开过了，就直接输出这个串；否则就继续展开。

因为题目中保证了 每行输出不超过1000，所以我们递归的次数怎么都不会超过 1000 （不过不知道luogu民间数据怎么卡的，最后一个点一直跑不过去，但官方数据真的太水了......）

因此时间至多是 \(O(\omega n)\) （\(\omega\) 为最长行的长度）

代码

---

D1T2 填树

祭奠我考场上打错了快读但依旧水了10分（和没打错一样的分数）

考虑一个 \(O(nK)\) 的做法：

我们枚举值域的最小值 \(l\)，并求出值域为 \([l,l+K]\) 的方案数

但由于 \(l\) 不一定能取到，我们就还要求出 \([l+1,l+K]\) 的方案数，两者容斥（前者减去后者）可以得到：最小值为 \(l\) 的方案数

求方案数是一个典型的 树形DP，可以 \(O(n)\) 完成

下面我们要考虑将它优化为 \(O(n^3)\):

当只有一个点时，它的方案数显然为：它可取的值域 与 限定的值域 求交

那么我们可以画出一个方案数关于最小值 \(l\) 的函数，如下图：

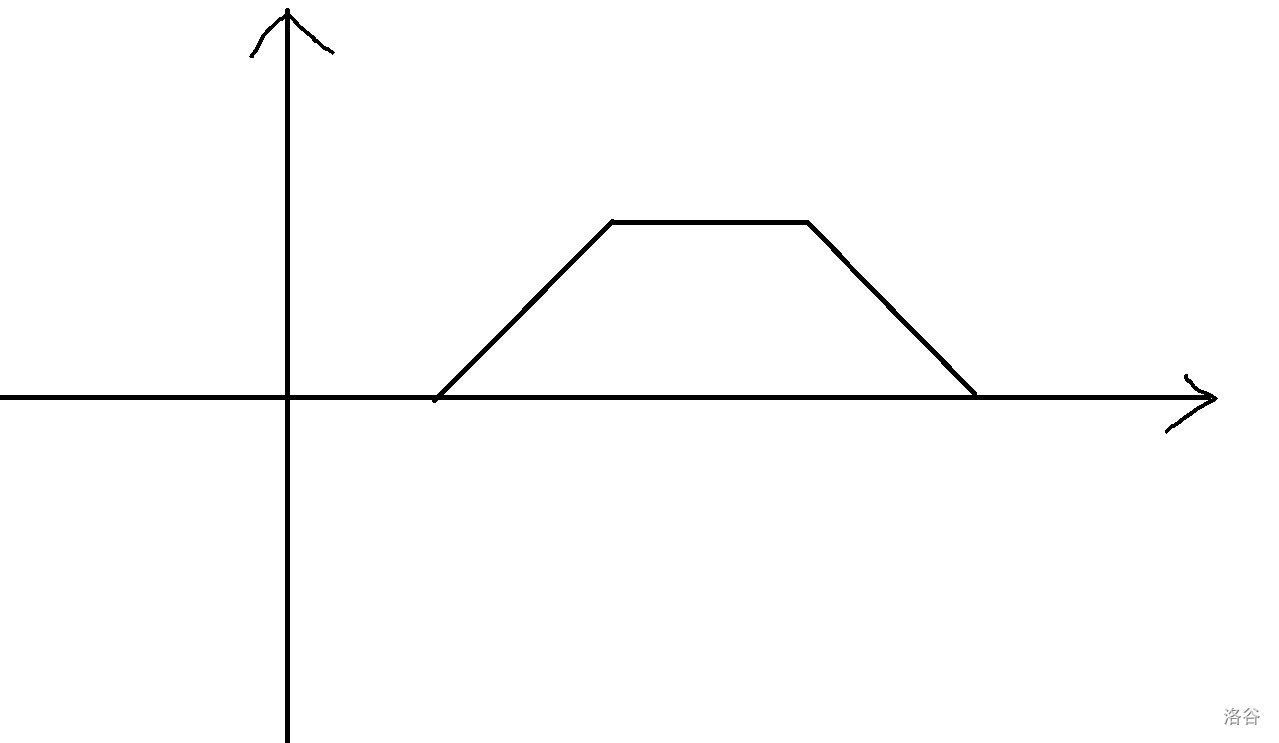
它其实是由 一个斜率为 \(1\) 的一次函数，一段平台，一段斜率为 \(-1\) 的一次函数 组成的

那么考虑多点，一个最小值 \(l\) 的方案数其实就是：选择某些点（一条路径），它们在 \(l\) 上的点值相乘，然后将所有路径的方案数累加

实际上，因为一个点的方案数的多项式是确定的，那么我们可以将选择的点的多项式乘起来，然后再把所有得到的多项式相加，就可以得到一个确定的多项式：代入任意最小值 \(l\) 就可以得到整棵树的方案数

而且这个多项式最高为 \(n\) 次

那么我们就可以用拉格朗日插值求出任意 \(l\) 的方案数

但这样还是要 \(K\) 次查询，我们就考虑用多项式前缀和，那么我们要插的多项式就变成 \(n+1\) 次的，只需要查询能取到的最大的最小值对应的函数值即可

由于每个点的函数是分段函数（最多三段），因此我们需要将值域拆成若干段，每段都进行一次操作：

\[L_i,\ R_i,\ L_i-K,\ R_i-K \]

这就是每个点要拆出来的区间的端点

至于权值和，做法类似，但因为一个点的权值计算是一个二次函数，而一条路径上的点的权值和不是直接相乘，而是类似于 方案数 \(\times\) 一个点的权值 再相加，因此函数最高次应为 \(n+2\)

代码

---

D1T3 学术社区

推荐两篇题解：

波波的题解

出题人 itst 的题解

性质 ABC

显然，A B louxia 可以转化为一条 \(B\) 指向 \(A\) 的边（因为 \(A\) 可能还要成为接收点）

对于学术性消息，就可以建一个超级源点 \(T\)，转化为 \(T\) 指向 \(A\) 的边

那么我们每次从 \(T\) 出发，经过一条边就表示某条楼下型消息被选择（当然如果出发点是 \(T\) 的边就是表示某条学术性消息被选择），停留在一个点 \(A\) 就表示这一连串最后发言的人是 \(A\)

因为又有 性质 B：所有楼上楼下型消息都一定是符合实际的，那么这个问题就转化成：构造路径覆盖的方案

算法模型应该为 欧拉回路，但我们发现，一些点 \(A\) 可能存在入度大于出度的情况，假设他们的差为 \(d\)，那我们就从 \(A\) 连 \(d\) 条边到 \(T\)，这可以理解为在 \(A\) 停止，然后回到 \(T\) 重新开始一段路径

那么排列应该就是长这样：学术 -> 楼下 -> ... -> 楼下 -> 学术 -> 楼下 -> ... -> 楼下 -> ...

而一定不存在某个点出度大于入度的情况，因为毕竟都保证了每个 楼下型消息 都是 符合实际的

性质 AC

不保证每个 楼下型消息 都是 符合实际的

那么就会出现某些点 \(A\) 出度大于入度的情况，对于这些额外的（出度减入度条）楼下型消息就无法产生贡献，那么答案就有一个下界，我们就可以构造一个方案符合这个下界

解决方法是：延续之前的方法，对于出度大于入度（设差为 \(d\)）的点 \(A\)，构造 \(d\) 条由 \(T\) 指向 \(A\) 的边，这样就说明不能选了

性质 BC

性质 \(C\) 终于要出场了！其实他的意思就是不会同时出现 A B loushang 和 B A louxia 的消息

那么我们就可以构造一条路径为 楼上 -> ... -> 学术 -> ... 楼下

同样是延续上面的思路，不过这次我们需要建立一个分层图 \(G_1\) 和 \(G_2\)，每个点在两层图中都有一个对应的点，对于 A B loushang，就在 \(G_1\) 中建立一条边 \(A \rightarrow B\)，对于 A B louxia，就在 \(G_2\) 建立一条边 \(B \rightarrow A\)，对于 A xueshu，就从 \(G_1\) 的 \(A\) 指向 \(G_2\) 的 \(A\) 点建一条边

然后仍然沿用 欧拉回路 的做法，不过超级源点 \(T\) 连向 \(G_1\) 中的每个点，\(G_2\) 中的每个点连向 \(T\)，再平衡一下入出度即可

性质 C

其实我们可以想一件事，对于那些无法贡献的楼上或楼下型消息，如果我们直接将它当成学术消息，那这样答案的下界就有可能被提升了

比如说，对于一条 A B loushang，如果我们舍弃它，就是 \(G_1\) 中 \(B\) 的入度减一，\(G_2\) 中的 \(A\) 入度加一，那么 \(B_1\) 和 \(A_2\) 的点都松弛了一，答案下界也上升了一

那我们就要尽可能多地选择这种边，我们考虑用最大流来求，建图方法为：

• 对于 \(G_1\) 中 入度大于出度 （差设为 \(d\)） 的点 \(u\)，连接一条 \(S\) 到 \(u\) 的边，流量为 \(d\)

• 对于 \(G_2\) 中 出度大于入度 （差设为 \(d\)） 的点 \(u\)，连接一条 \(u\) 到 \(T\) 的边，流量为 \(d\)

• 对于 A B loushang 连接一条 \(B_1\) 到 \(A_2\) 的边，流量为 \(1\)

• 对于 A B louxia 连接一条 \(A_1\) 到 \(B_2\) 的边，流量为 \(1\)

跑完最大流后，那些残余流量为 \(0\) 的边就是我们要“舍弃”的边

然后我们再按照上面的方法（性质 AC 和 BC）做欧拉回路即可

正解

没了性质 C，就可能有一些能相互指的消息

但其实对于 A B loushang 与 B A louxia 一起出现时，把它们组合在一起一定不劣

那他们就可以合起来充当一个学术消息的作用，但依旧有贡献（为 \(2\)）

这样就又重新转换为上面的问题了

代码

---

D2T1 卡牌

听说是 寿司晚宴 的经典套路，但本蒟蒻根本就没做过......

我们不难发现，对于 \(<\sqrt n\) 的质数，只有区区 \(13\) 个

这似乎就在暗示我们用根号分治，分开讨论大小质数，然后做状压DP？

正难则反，我们考虑答案计算方法为：全部方案数 \(-\) 有部分要求的质数没选的方案数

这显然是一个容斥

那我们就考虑对前 \(13\) 个质数选出一些质数进行状压，用 \(S\) 来表示，并令 \(cnt\) 表示给出的数中不为 \(S\) 任意一个质数的倍数的个数

我们考虑计算：\(S\) 上的质数都没被选择的方案数，就是 \(2^{cnt}\)，然后容斥

而对于 \(>\sqrt n\) 的质数，由于每个数最多只会出现一次，那么我们就不需要容斥，而是在对前 \(13\) 个质数进行容斥时都强制至少选择一个，如果它在那 \(cnt\) 个数中出现 \(x\) 次，那么每次容斥的方案数就会变为 \(2^{cnt-x}(2^x-1)\)

这样我们就做完了，至于说求出“不为 \(S\) 任意一个质数的倍数的个数”，预处理就可以了

代码

---

D2T2 序列变换

讲真，做完之后觉得似乎真没那么难

连年考括号序列，按照套路，我们上来就给它建个括号树

对于每个操作，括号树的变换如下：

• 操作 1：即选择两个同一层的结点 \(u, v\)，将 \(v\) 所有的儿子都连接到 \(u\) 上，再将 \(v\) 连到 \(u\)（也就是将 \(v\) 向下移动一层了），这里的代价为 \(x\times val_u+y\times val_v\)

• 操作 2：即任意一个结点的儿子的位置可以任意互换

我们最后的目的就是想要将这棵树弄成一条链

首先有一个贪心是：显然对于某一层，它要进行操作的结点是固定的，那我们就可以考虑从浅到深进行处理。这样每次处理某一层时，所有的结点都连接在同一个父亲上，那么我们就可以进行若干次操作2，这样的自由度是最大的

接着，我们观察到 \(x,y\leq 1\)，因此我们可以考虑分类讨论：

• \(x=0,\ y=0\)

显然答案为 \(0\)

• \(x=0,\ y=1\)

说明只有被往下移动的结点才会产生贡献，而保留下来的结点不会贡献，那么我们就考虑留下代价最大的结点，其他结点就移到下一层继续操作

• \(x=1,\ y=1\)

先讲这个是因为它与上一个类似

相较与上一个，“被留下”的结点也需要贡献，但其实我们可以借助一个“跳板”，这个跳板就是这一层代价最小的结点：我们可以将所有非最大也非最小的结点先挂在代价最小的结点下面，最后再将代价最小的结点挂到代价最大的结点下面，这样我们产生的贡献就是：当前层所有结点的代价和，加上 最小代价 \(\times\) (结点个数 \(-\ 2\))

• \(x=1,\ y=0\)

这个是最麻烦的

首先，所有数中，只有放在最底下的那个结点不需要贡献，其他的结点至少要贡献一次，那么我们肯定让最底下的结点代价尽可能大

对于结点数 \(>2\) 的层，我们考虑像上一个那样，借助最小值当“跳板”，最后留下一个非最大也非最小的结点

但如果结点数 \(=2\)，那应该传最大值还是最小值？

我们想象一下处理这个括号树的样子，就是先跳过一段结点为 \(1\) 的层，然后遇到连续一段结点为 \(2\) 的层，然后继续增长，最后一步步减剩 \(1\)；当然，在下降的过程中也会遇到结点数为 \(2\) 的层，但这时候一定就是直接传最大值下去就行了

这段连续的 \(2\) 最终只会有一个结点传到下面，一种想法就是枚举下传的结点，但这样是 \(O(n^2)\) 的，跑不过去

其实我们仔细想一下，特殊的结点就是那些被当跳板的最小值，以及被传递到最后的最大值（不用贡献），其他每个结点都要贡献一次

那么这段连续的 \(2\)，要么是一直传递最小值下去，给后面的当跳板降低贡献，要么是一直传递最大值下去，让非常非常大的结点不用贡献

那么我们只需要分两类来讨论即可

代码

---

D2T3 最大权独立集问题

一种很妙的树形DP，关键就是给转移留出可变的空间，让某个地方的贡献先暂时不去计算

• 定义：

设 \(f_{u,v}\) 表示将 \(r=\text{lca}(u, v)\) 为根的子树的所有边，以及 \(r\) 与其父亲 \(x\) 的边都断开，且最后 \(u\) 停留在 \(x\) 处，\(x\) 停留在 \(v\) 处，所需的最小贡献，但对于 \(x\) 产生的贡献暂不算入 \(f_{u,v}\) 中

搞定了这个定义，我们就开始进行分类讨论：令 \(now\) 为当前转移的结点；\(sz\) 为 \(now\) 的儿子数量；\(d_u\) 表示最初 \(u\) 结点的代价

• \(sz = 0\)

说明 \(now\) 是叶子，那么只有一种操作：

\[f_{now,now}=d_{now} \]

• \(sz = 1\)

令它的儿子为 \(s\)

因为 \(now\) 只有一个儿子，又要使 \(\text{lca}(u,v)=now\)，所以 \(u\) 或 \(v\) 中有一个是 \(now\)

• • \(u=now\)

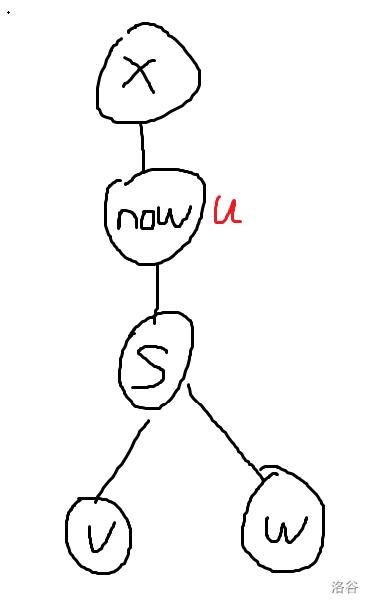
如图，要使 \(now\) 移到 \(x\) 处，那么第一步操作就是先交换 \(now, x\)

然后要将位于原本 \(now\) 的位置的 \(x\) 移到 \(v\)，且将以 \(s\) 为根的子树断开所有边，那么我们就需要找到一个 \(w\)，使得 \(f_{w,v}\) 最小

因此有转移方程：

\[f_{now,v}=\min(d_{now}+f_{w,v})\ _{(\text{lca}(w,v) = s)} \]

• • \(v=now\)

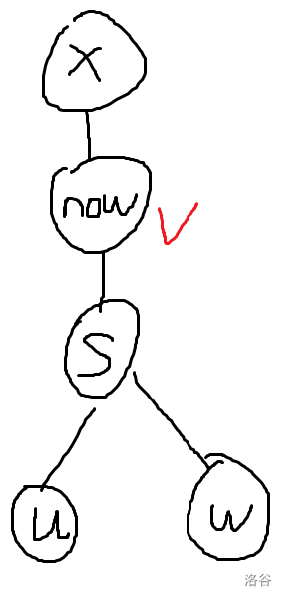
这次就应该先将以 \(s\) 为根的子树所有边断开（同时将 \(u\) 移到 \(now\) 的位置），最后再交换 \(u,x\)

但注意到，此时由于之前没有将 \(now\) 计入到断开子树 \(s\) 的代价中，此时我们要重新加上这个贡献，有转态转移方程：

\[f_{u,now}=\min(f_{u,w}+d_{now}\times (dep_w-dep_{now})+d_u)\ _{(\text{lca}(u,w) = s)} \]

到这里，所有操作的总时间复杂度都是 \(O(n^2)\) 的

• \(sz = 2\)

令 \(now\) 的两个儿子为 \(s_1,\ s_2\)

注意：这里的 \(s_1,\ s_2\) 没有顺序的差别，因此下面提到的 \(s_1,\ s_2\) 只是区分两个儿子，但实际上需要互换再进行一次转移的

这时候的讨论就更多了：

• • \(u=now,\ v\not = now\)

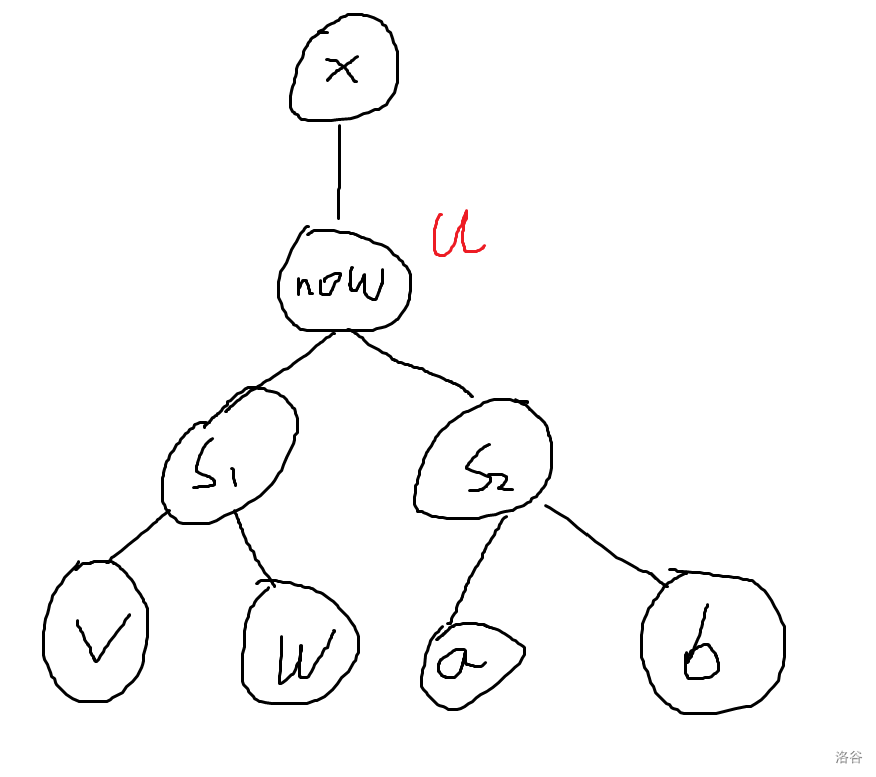
操作顺序为：交换 \(now, x\)，然后将 \(x\) 移动到 \(v\)（同时也断开了 \(s_1\) 内所有的边），最后断开 \(s_2\) 内所有的边

转移方程为：

\[f_{now,v}=\min(d_{now}+f_{w,v}+f_{a,b}+d_{w}\times (dep_b-dep_{now}))\ _{(\text{lca}(w,v)=s_1,\ \text{lca}(a,b)=s_2)} \]

但这个转移似乎是 \(O(n^4)\) 的？

但其实我们可以发现，这个转移可以分成 \([a,b], [w,b],[w,v]\) 这三段

也就是说，我们可以先求出只与 \(b\) 有关，\([a,b]\) 段的最小值

然后通过这个再求出只与 \(w\) 有关，\([w,b]\) 段的最小值

最后再求出 \([w,v]\) 段的最小值

这样就能转化为 \(O(n^2)\) 的了

• • \(u\not = now,\ v = now\)

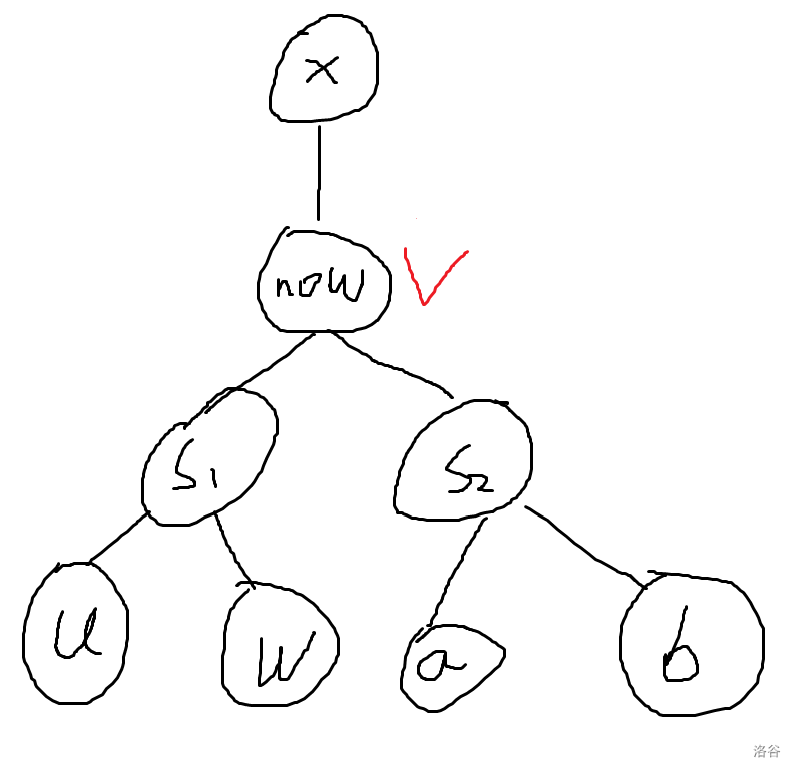
操作顺序为：先将 \(s_2\) 的所有边断开，再将 \(u\) 移到 \(now\) 原本所在的位置（同时将 \(s_1\) 的所有边断开），最后交换 \(u,x\)

转移方程为：

\[f_{u, now}=\min(f_{a,b}+d_{now}\times (dep_b-dep_{now})+f_{u,w}+d_a\times (dep_w-dep_{now})+d_u)\ _{(\text{lca}(u,w)=s_1,\ \text{lca}(a,b)=s_2)} \]

一样的，我们可以通过分段操作化为 \(O(n^2)\)

• • \(u\not=now,\ v\not= now\)

显然 \(u,v\) 分别在 \(now\) 的两个儿子的子树内

操作顺序为：先将 \(u\) 移到 \(now\) 的位置上（同时将 \(s_1\) 的所有边断开），然后交换 \(u,x\)，最后将 \(x\) 移到 \(v\) 的位置上（同时将 \(s_2\) 的所有边断开）

转移方程为：

\[f_{u,v}=\min(f_{u,w}+d_{now}\times (dep_w-dep_{now})+d_u+f_{a,v})\ _{(\text{lca}(u,w)=s_1,\ \text{lca}(a,v)=s_2)} \]

最后转移到根节点 \(1\) 处，但它没有父节点，怎么转移？

其实只需要灵活变通就行了：

• 若 \(1\) 只有 \(1\) 个儿子

则答案转移为：

\[and=\min(f_{u,v}+d_1\times(dep_v-dep_1))\ _{\text{lca(u,v)}=s} \]

• 若 \(1\) 有 \(2\) 个儿子

则答案转移为：

\[ans=\min(f_{u,v}+d_1\times (dep_v-dep_1)+f_{a,b}+d_u\times (dep_b-dep_1))\ _{(\text{lca}(u,v)=s_1,\ \text{lca}(a,b)=s_2)} \]

代码