Edges in MST
思路:
首先我们得明白 Kruskal 的操作过程:对最小的边进行贪心
那我们就有一个想法,对于一条在 MST 中的边 \(e\) ,只有与它权值相同的边才有可能去替换它
那我们就统计图中某个权值 \(val\) 的边数 \(cnt\),再统计实际选入 MST 里的权值为 \(val\) 的边数 \(ch\)
显然,如果 \(cnt==ch\) ,那么这种边权的边一定都要选;如果 \(ch==0\) ,代表这种边权的边一定都不用选
那万一这两种情况都不是,是不是就是可能选了?
显然不是的,例如下图:
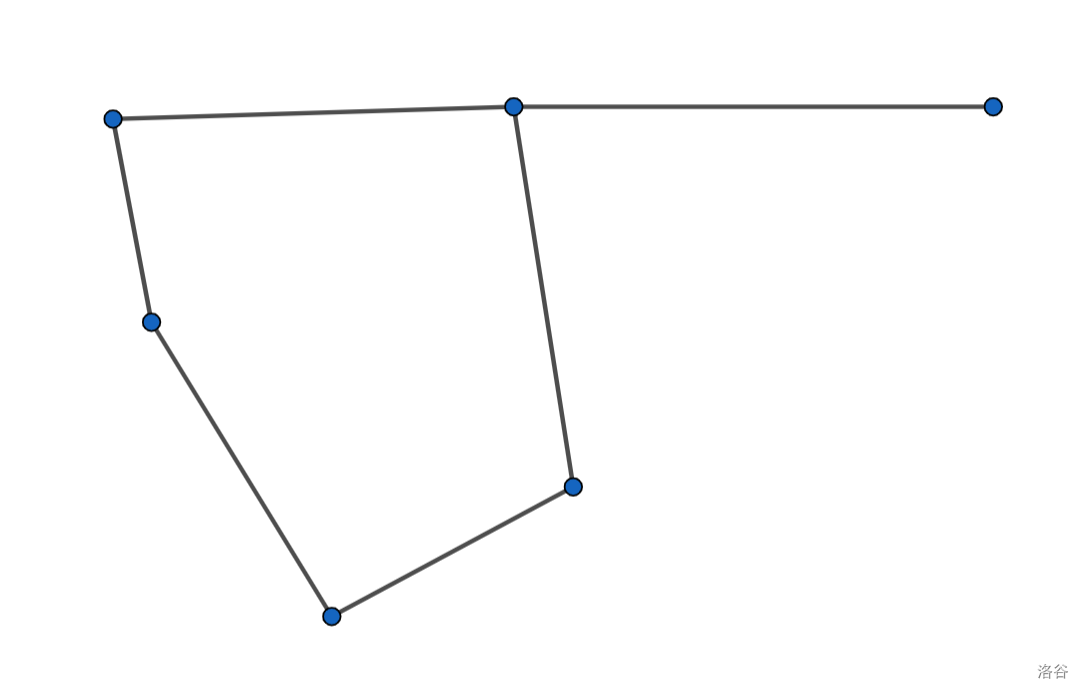
假设边权都是 1 ,如果我们单看左边那个环,确实是都是 可能选中;但再看环外伸出的那条边,如果不选它,我们就连生成树都做不出来了
因此我们需要换个思路
正解:
显然,对于小于当前边权值 \(val\) 的边,它们之中无论选那些边,对于我决策当前边是等价的:即连通块的情况相同
所以我们就考虑将相同的边放在一起决策
对于一条连接 \(u,v\) 的边,如果 \(u,v\) 已经在同一个连通块内,显然这条边是一定不用选的,因为前面边权更小的边一定更优,我们就不再继续考虑这些边
而对于连接不同连通块的边,它有可能是 必选项,也可能是 有可能选项
到这里我们不难看出,如果不选择某一条边,会导致两个连通块无法连通(仅限于考虑权值相同的边的情况下),那它就是必选项
换而言之,我们将连通块都缩成一个点,并加入权值相同的边,如果某条边是 桥(割边),那么它就是必选项
最后剩下的就是可能选的边
总结:
-
每次考虑权值相同的边
-
对于 \(u,v\) 已在同一个连通块的边,我们剔除它,不再继续考虑
-
将连通块缩点,加入剩下的边,跑一遍
tarjan求桥(割边) -
再正常跑最小生成树的步骤,得到新的连通块
代码:
#include<iostream>
#include<fstream>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<queue>
#include<map>
#include<set>
#include<bitset>
#define LL long long
inline int reads()
{
int sign = 1, re = 0; char c = getchar();
while(c < '0' || c > '9'){if(c == '-') sign = -1; c = getchar();}
while('0' <= c && c <= '9'){re = re * 10 + (c - '0'); c = getchar();}
return sign * re;
}
int n, m, fa[100005];
struct Node
{
int u, v, w, id, ans;
}r[100005];
inline bool cmp(Node a, Node b) {return a.w < b.w;}
inline bool cmpback(Node a, Node b) {return a.id < b.id;}
int finds(int now)
{
if(now == fa[now]) return now;
return fa[now] = finds(fa[now]);
}
inline bool check(int u, int v)
{
u = finds(u), v = finds(v);
if(u == v) return true;
else return false;
}
inline void match(int x, int y)
{
x = finds(x), y = finds(y);
if(x != y) fa[y] = x;
}
std::vector<std::pair<int, int> > eg[100005];
int dfn[100005], low[100005], dcnt;
void tarjan(int now, int la)
{
dfn[now] = low[now] = ++dcnt;
for(int i = 0; i < eg[now].size(); i++)
{
int to = eg[now][i].first;
if(eg[now][i].second == la) continue;
if(!dfn[to]) tarjan(to, eg[now][i].second), low[now] = std::min(low[now], low[to]);
else low[now] = std::min(low[now], dfn[to]);
if(low[to] > dfn[now]) r[eg[now][i].second].ans = 1;
}
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("test.in", "r", stdin);
freopen("test.out", "w", stdout);
#endif
n = reads(), m = reads();
for(int i = 1; i <= m; i++)
{
int u = reads(), v = reads(), w = reads();
r[i] = (Node){u, v, w, i, 0};
}
std::sort(r + 1, r + 1 + m, cmp);
for(int i = 1; i <= n; i++) fa[i] = i;
for(int i = 1; i <= m; i++)
{
int j = i;
while(r[j + 1].w == r[i].w) j++;
for(int k = i; k <= j; k++)
if(check(r[k].u, r[k].v)) r[k].ans = -1;
else eg[fa[r[k].u]].push_back(std::make_pair(fa[r[k].v], k)), eg[fa[r[k].v]].push_back(std::make_pair(fa[r[k].u], k));
for(int k = i; k <= j; k++)
if(r[k].ans != -1 && !dfn[fa[r[k].u]])
{
dcnt = 0;
tarjan(fa[r[k].u], 0);
}
for(int k = i; k <= j; k++)
eg[fa[r[k].u]].clear(), eg[fa[r[k].v]].clear(), low[fa[r[k].u]] = low[fa[r[k].v]] = dfn[fa[r[k].u]] = dfn[fa[r[k].v]] = 0;
for(int k = i; k <= j; k++)
match(r[k].u, r[k].v);
i = j;
}
std::sort(r + 1, r + 1 + m, cmpback);
for(int i = 1; i <= m; i++)
if(r[i].ans == -1) printf("none\n");
else if(r[i].ans == 1) printf("any\n");
else printf("at least one\n");
return 0;
}

