树分治
终于来填坑嘞
① 点分治
(俗称淀粉质)
通常用来解决树上路径问题
我们每次钦定一个点,并只统计经过这个点的路径;处理完后我们向其子树分治下去
每次选择的点都很关键,比如一条链,如果你一直选择它的端点,那我们的时间复杂度可能还是 \(O(n^2)\)
最优的决策点应该是树的重心,这样树的高度就保证在 \(O(\log n)\) 附近
找重心,就是要找到一个点 \(u\),满足它最大的子树大小在所有点内是最小的,记得它父亲往上的也算它的一棵子树,计算方法为:所有点数 减去 子树 \(u\) 的大小
void getrt(int now, int fa)
{
sz[now] = 1;
Mx[now] = 0;
for(int i = he[now]; i; i = r[i].nxt)
{
int to = r[i].to;
if(vis[to] || to == fa) continue;
getrt(to, now);
Mx[now] = std::max(Mx[now], sz[to]);
sz[now] += sz[to];
}
Mx[now] = std::max(Mx[now], tot - sz[now]);
if(Mx[now] < Mx[rt]) rt = now;
}
我们每分治到一个点 \(u\) 时,我们就将它每个子树内的点到 \(u\) 的路径计算出来,然后与之前处理过的子树的点匹配(因为要保证路径经过 \(u\)),看看有没有满足距离和为 \(d\) 的
处理完后我们就找到每棵子树的重心,分治下去,重复上述操作
和普通分治类似,时间复杂度是 \(O(n\log n)\) 的
按正常的点分治,我们将每条路径处理下来后,然后匹配对应的合法长度的路径,将贡献加起来
但由于相同颜色段的贡献只计算一次,因此合并的两条路径,如果初始边的颜色相同,就需要减去这个颜色的价值
我们递归到一个分治中心时,考虑按照出边的颜色依次进行 dfs,然后维护两颗线段树,下标代表路径长度,储存当前长度最大贡献;其中一棵储存的是出边颜色不同的路径,另一颗储存的是出边颜色相同的路径;当我们处理完一种颜色后,就将第二棵线段树合并到第一棵上
时间复杂度为 \(O(n\log^2 n)\)
② 按重心移动
这类题是用到了点分治的思想,将复杂度均摊到 \(O(n\log n)\)
这道题,我们要抓住的核心就是:让目前最大的路径变小。
而有几种情况是一定不能变小的:
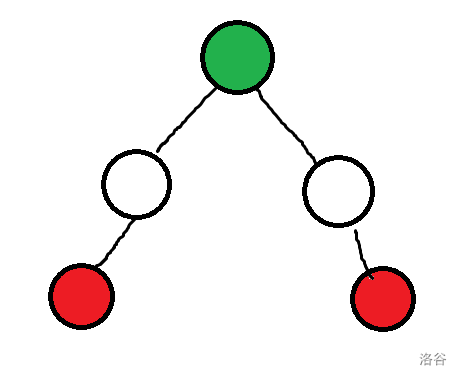
如图,绿点为 \(c\) ,红色是目前长度最大的路径 \(u,v\)
显然,如果 \(c\) 沿着 \(u,v\) 移动,答案一定不会变小;反之,如果走向 \(c\) 的其他子树,那答案一定变大
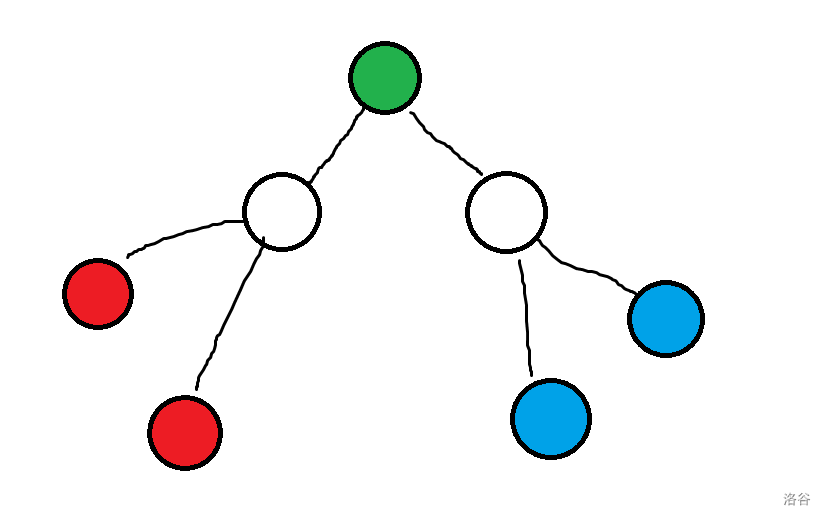
如图,绿点为 \(c\) ,红、蓝色都是目前长度最大的路径 \(u_1,v_1\),\(u_2, v_2\)
显然,如果 \(c\) 向红色那边移动,那么蓝色点的长度就会增加;反之亦然;因此这种也不能移动
因此,如果我们要移动到 \(c\) 的子树 \(v\),必须满足有且仅有一对最大点,且两端属于 \(v\) 子树
因此,我们每次 \(c\) 的选择应该要是重心,这样只需要跳 \(\log n\) 次
而每次求到 \(c\) 的路径都需要遍历一整棵树,是 \(O(n)\) 的;这样我们就做到复杂度为 \(O(n\log n)\)
题意:一棵树,有点权 \(val_i\) 与边权,定义 \(dis(u,v)\) 为 \(u\) 到 \(v\) 简单路径上的边权和,现在要找出一个点 \(c\),使得 \(\sum_{i=1}^n dis(i,c)^{1.5}val_i\) 最小(即带权重心)
对于一条路径 \((a,b)\),如果 \(x\in(a,b)\),那么有关于 \(x\) 的函数 \(dis(x,i)^{1.5}\) 为下凸函数(\(i\) 为 树任意一个结点)
因此,在 \((a,b)\) 上,答案也应该是一个关于 \(c\) 的下凸函数(因为下凸函数的和仍为下凸函数)
因此,如果我们计算出当前点 \(now\) 的答案,那么最小答案一定会是在 \(now\) 中的某一个子树中;而如果往其他子树移动,答案必然增大(这个思想可类比上一题)
那我们怎么找出唯一一个答案会变小的子树呢?
我们考虑从 \(now\) 移向某个子树 \(to\),移动距离为 \(x\),那么答案应该变为:
但我们不可能将每个子树的答案都求出来,这样还不如 \(O(n^2)\)
有增量,我们就考虑求导,得:
我们可以将 \(x=0\),这样就能得到将要向 \(to\) 移动时答案的增量
也就是说,对于每次点分治,我们都求出每个点的 \(dis(v,rt)^{0.5}val_v\),加到对应的子树上,令其为 \(w_{to}\),如果其他子树 \(w\) 的和 减去 \(w_{to}\) 小于 \(0\),那么我们就向子树 \(to\) 移动
这样我们只用移动 \(\log n\) 次, 每次遍历整棵树即可
由于带权重心可能在边上(即不能刚好在点上),我们要记录两个相邻的点,最后计算一下哪个答案最小即可
③ 边分治
类比点分治,边分治统计的是“经过某条边的路径”
而边分治有他的优势所在,就是在统计答案时,它只会涉及两个子树,对于一些如最值的合并,我们只需要对两个子树进行双指针移动
边的选取与点分治类似,尽量使最大的子树的结点数最小
但对于一些如菊花图这样的图,很容易就被卡回 \(O(n^2)\)
因此,我们要对树三度化,有两种方法:(以下方法和图片选自 JhinLZH大佬的博客)
-
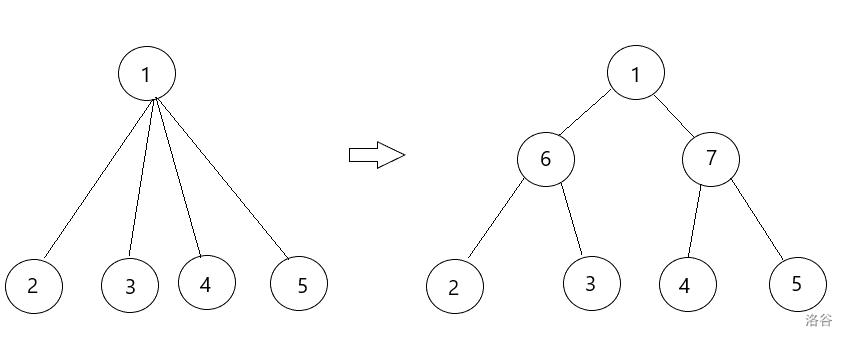
从 \(1\) 号结点开始枚举每个点,对于一个点 \(x\),如果他的子节点数小于等于 \(2\),那么直接连边即可;否则我们新建两个点,将 \(x\) 连向这两个点,并将 \(x\) 的子节点按奇偶分类暂时归为这两个新建点的子节点。
为了不影响原树深度等信息,我们将连向新建点的边权设为 \(0\)。这样新建树每条原树边会被存 \(\log n\) 次,所以空间复杂度是 \(O(n\log n)\),新建节点数 \(O(n)\)
- 我们依旧从 \(1\) 号结点遍历整棵树,对于一个点 \(x\),我们先将一个儿子与 \(x\) 相连,然后让
lst=x;接下来的儿子 \(u\)(除了最后一个),我们先新增一个结点与lst相连,然后 \(u\) 与新节点相连,再让lst更新为这个新节点;对于最后一个儿子,直连上目前的lst即可。这样的空间复杂度则是 \(O(n)\) 级别的
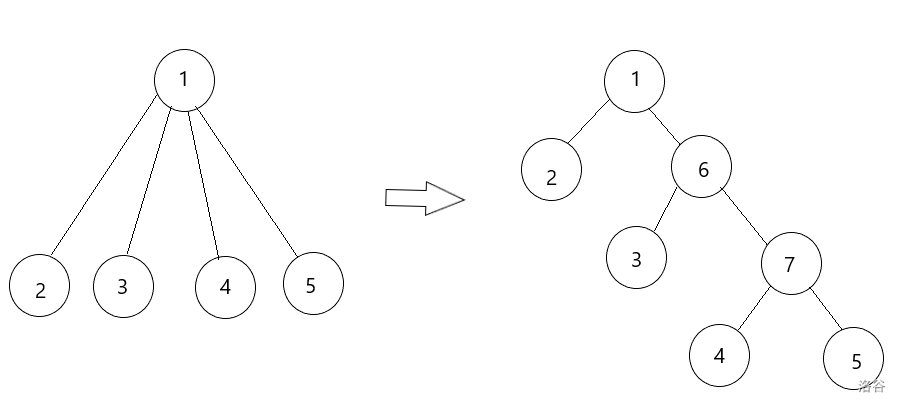
我们要注意,新增节点的权值应设为其父亲的权值,而连向新节点的边的边权应设为 \(0\)
还有,在统计答案时,由于深度是节点个数,应该为 \(Mx+r[now].w+1\);而如果指针没有移动,就不能统计答案!
④ 动态点分治
从上面的例题我们不难看出,一般的点分治只能解决静态问题。
但我们不难发现,对于一个结点,它在点分治中只会被用到 \(\log n\) 次。
所以,如果修改一个点的信息,那么实际上只会影响 \(\log n\) 个重心。
如果我们按重心遍历的顺序连边,可以发现它是一个树形结构,这就是点分树。
而当我们修改一个点的信息时,其实只需要修改点分树上它到根的路径上的重心信息。
再配合一些数据结构(维护信息),我们就可以做到 \(O(n\log^2 n)\) 的复杂度。
没有修改的话,那就是一个简单的点分治模板题。
考虑点分治时我们用到哪些信息:到重心不同距离的权值和、重心的每个儿子的子树到重心不同距离的权值和(用于去重)。
那我们修改的话也是修改这些信息,我们就可以考虑用动态开点线段树来维护。
这题没有修改的话也是一道点分治经典题。 (不,没有修改应该是求直径)
考虑要维护的信息:连通块结点到重心的距离,子树内到重心的最大值和次大值。
我们可以用可删堆来实现。
除了维护上面两个信息,我们还要维护一个全局最大值,具体就是将每个重心的最大值加次大值加到一个可删堆里。
可删堆的实现方式:用两个优先队列 \(a,b\)。当删除一个数时,我们不是从 \(a\) 删掉,而是将要删的数加入到 \(b\) 中;当要取数出来时,如果 \(a,b\) 的堆顶的数相同,就同时弹出。
终于填完坑嘞!

