高斯消元
高斯消元是一类用来求解 线性方程组(\(n\) 元一次方程组) 的算法
Gauss 消元
核心思想其实就是代入消元
我们考虑每次将一个未知数的所有系数消为 \(0\),只留下一个方程的这位系数不为 \(0\)
步骤如下:设当前消到第 \(i\) 个未知数
-
从 \(i\) 个方程开始找,找到第一个不为第 \(i\) 项的系数不为 \(0\) 的方程 \(id\),退出循环,交换第 \(i\) 个方程 and 第 \(id\) 个方程
-
然后对 \([i,n]\) 的所有方程进行消元,设目前处理到第 \(j\) 个方程,则令 \(mul = a[j][i] / a[i][i]\),对方程 \(j\) 的每个项的系数 \(k\ (k \ge i)\) 都减去 \(a[i][k] * mul\)
这就是加减消元的过程
但由于我们只消掉了一半的未知数(因为每次都从第 \(i\) 个方程往后消,前面的没有消到),所以它会长这样(假设有解)
(其中 \(a\) 表示系数,\(b\) 表示常数)
因此我们还要回代,也就是先求出第 \(n\) 个未知数 \(x_n=b_n/a_{n,n}\);
然后第 \(n-1\) 个方程的常数 \(b_{n-1}\) 减去 \(a_{n-1,n}\times x_n\),然后再求出第 \(n-1\) 个未知数 \(x_{n-1}=b_{n-1}/a_{n-1,n-1}\)
然后第 \(n-2\) 个方程的常数 \(b_{n-2}\) 减去 \(a_{n-2,n}\times x_n+a_{n-2,n-1}\times x_{n-1}\),然后再求出第 \(n-2\) 个未知数 \(x_{n-2}=b_{n-2}/a_{n-2,n-2}\)
...
以此类推,最后求出第 \(1\) 个未知数 \(x_1\)
至于无解:就是在消元的过程中找不到系数不为 \(0\) 的项,代表当前的未知数无解
时间复杂度高达 \(O(n^3)\)
高斯-约旦消元
听说这玩意的精度更好,因为不会产生回代的计算误差(也不知道是不是真的)
但根据 lby 大佬说的:
你这方法的常数比普通的 Gauss 消元大一倍呢
高斯-约旦消元,就是一种不需要回代的消元方法
它与普通的 Gauss消元 的区别就在于,第二步中我们将对 \([1,n]\) 但不包括第 \(i\) 个的方程都进行消元(其他步骤相同)
这样我们第 \(i\) 个方程就只有第 \(i\) 项上是有系数的
答案直接输出 \(b_i/a_{i,i}\) 即可
带状矩阵消元
这在 有后效性的期望DP 应用比较多
有时候,我们通过对系数进行一定调整,会发现我们需要消掉的系数会长这样:
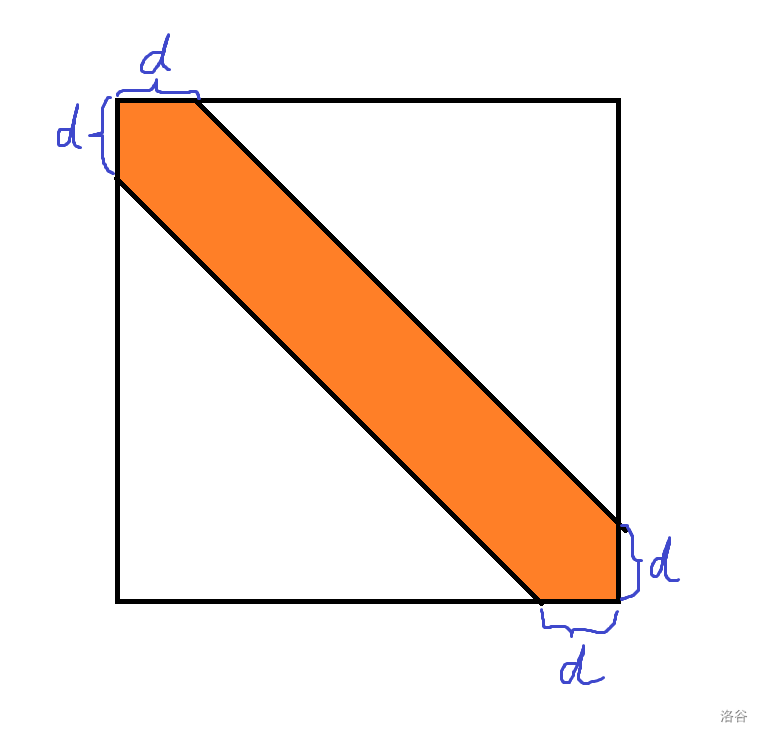
橙色部分就是我们要消去的部分
考虑用普通的 Gauss消元,我们可以发现,每次我们最多只需要向下消 \(d\) 个方程
而且每个方程我们也只需要消去 \([i,i+d]\) 上面的系数即可,因为第 \(i\) 个方程 \(i+d\) 后面的系数都为 \(0\),消了和没消一样
这样我们就可以做到 \(O(nd^2)\) 进行消元
(记得要回代!)
关键部分(加减消元)的代码:
for(int i = 1; i <= n; i++)
{
for(int j = i + 1; j <= std::min(i + d, n); j++)
{
double mul = a[j][i] / a[i][i];
for(int k = i; k <= std::min(i + d, n); k++)
a[j][k] -= a[i][k] * mul;
a[j][n + 1] -= a[i][n + 1] * mul; //记得这里要把常数也减一下!
}
}
但有一个棘手的问题,如果处理到第 \(i\) 个未知数时,第 \(i\) 个方程的系数 \(a_{i,i}\) 为 \(0\) ,我们就要进行交换,但一交换就会破坏带状结构,这样就无法做到 \(O(nd^2)\)
但实际上,对应 DP 这类问题,这种情况是不存在的,可以证明,参考这里
但其实还有一种方法,我们考虑交换后会变成什么情形:
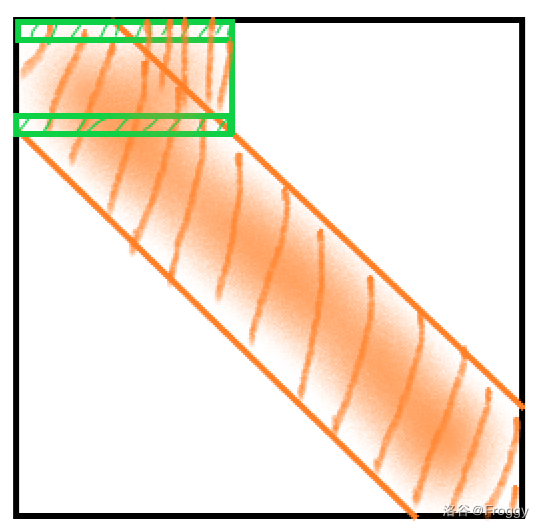
(借用 Froggy 大佬的图)
最坏情况下,我们交换后会让带的宽扩展 \(d\)
那其实我们在消系数的时候一直消到 \(i+d*2\) 不就行了
也就多一倍的常数而已
因此我们可以这样做:
for(int i = 1; i <= n; i++)
{
int id = i;
for(int j = i; j <= std::min(i + d, n); j++)
if(a[j][i])
{
id = j;
break;
}
std::swap(a[i], a[id]);
if(!a[i]) continue;
for(int j = i + 1; j <= std::min(i + d, n); j++)
{
double mul = a[j][i] / a[i][i];
for(int k = i; k <= std::min(i + (d << 1), n); k++)
a[j][k] -= a[i][k] * mul;
a[j][n + 1] -= a[i][n + 1] * mul;
}
}
主元法
这种方法有一定的要求:在网格图中,且边界外的期望值已知(一般为 \(0\))
可以将 \(O((nm)^3)\) 的普通高消优化到 \(O(n^3)\) 或 \(O(m^3)\)
问题引入:
在一个 \(n\times m\) 的网格图中,人物初始位置为 \((x,y)\),它每次可以上下左右移动,概率为 \(p_1,p_2,p_3,p_4\),问它走到边界外的期望步数(到边界外即停止)
如果 \(n,m\) 小一点,我们就可以根据朴素的高消做:
\(f_{i,j} = f_{i-1,j}p_1+f_{i+1,j}p_2+f_{i,j-1}p3+f_{i,j+1}p4+1\)
但如果 \(n,m\le 100\) 呢?
显然这会直接炸掉
但我们注意到,边界外的期望始终为 \(0\)
那我们就考虑通过只设一列为未知数,剩下的格子由这些未知数来表示
如 \(5\times 4\) 的图:

我们将第一列依次设为 \(x_1,x_2,x_3,x_4\)
那么因为 \(x_1(f_{1,1})=f_{0,1}p_1+f_{2,1}p_2+f_{1,0}p3+f_{1,2}p4+1=x_2p_2+f_{1,2}+1\)
因此 \(f_{1,2}=\frac{x_1-x_2p_2-1}{p_4}\)
剩下的依次类推,每次都是一列一列地向右推进
到最后时,我们表示出第 \(m+1\) 列的格子,由于这些格子已经在边界外了,也就是它们就为 \(0\),这样我们就能得到 \(n\) 个方程
这样我们只需要对我们设的未知数进行高斯消元即可,最后代入到 \(f_{x,y}\) 的表达式算出答案即可
那如果对于每次可以向八个方向移动的题呢?那我们直接对第一行和第一列都设成未知数即可,然后就去表示即可

