线性基
线性基是用来解决子集异或一类问题的算法
先放个大佬写的详细解析
(我是学着ta的来写的)
先引入一些概念(下面的大写字母都表示一个“无符号整数集”):
张成:
(看着像个人名...)
若 \(T\subseteq S\) ,则所有这样的子集 \(T\) 的异或和组成的集合为 \(S\) 的张成,记作 \(span(S)\)
线性相关:
若存在一个元素 \(a\in S\) ,使得 \(S\) 去掉这个元素后的集合 \(S'\) 的张成 \(span(S')\) 包含 \(a\) ,则称集合 \(S\) 线性相关
通俗地,这可以表示为:存在一个元素 \(a\in S\) ,可以被剩下的若干个元素异或起来得到
如果不存在这样的一个元素,则称这个集合 \(S\) 线性无关
显然,对于一个线性相关的集合 \(S\) ,有 \(span(S)=span(S')\)
线性基:
当集合 \(P\) 满足以下条件时,我们称 \(P\) 是 \(S\) 的线性基:
-
- \(S\subseteq span(P)\)
-
- \(P\) 线性无关
而 \(P\) 拥有以下性质:
-
- \(P\) 的任何一个真子集都不是线性基(也就是说 \(P\) 的长度是唯一确定的)
-
- \(S\) 中任意一个元素,可以唯一表示为 \(P\) 中若干个元素的异或和
(这个性质很重要,用于一个数是否存在于 \(S\) 中的判断等)
- \(S\) 中任意一个元素,可以唯一表示为 \(P\) 中若干个元素的异或和
线性基的构造:
两种构造方法:
这两种线性基都需要满足以下条件:
-
- 若 \(p[i]=0\) ,则只有满足 \(j>i\) 的 \(p[j]\) 的第 \(i\) 位才可能上为 1 ;
-
- 若 \(p[i]\not = 0\) ,则 \(p[i]\) 更高的二进制位(即 \(>i\) 的二进制位)一定为 0 ;\(p[i]\) 更低的二进制位(即 \(<i\) 的二进制位)可能为 1
- 对于每个新插入的数 \(a\) ,找出其二进制下最高的 1 所在的位置 \(i\) ,若 \(p[i]=0\) ,则让 \(p[i]=a\) ;否则将 \(a\) 异或上 \(p[i]\) ,重复上述步骤
针对这种方法的模板代码
(记住这种方法求最大值时要进行贪心)
- 第二种构造出来的线性基还需要满足以下性质:
-
- 若 \(p[i]\not = 0\) ,则整个 \(p\) 数组中只有 \(p[i]\) 的第 \(i\) 位上为 1
则构造方法为:
-
- 若 \(p[i]\not = 0\) ,则将 \(a\) 异或上 \(p[i]\)
-
- 若 \(p[i]=0\)
-
对于 \(j\in [0,i)\) ,若 \(a\) 的第 \(j\) 位为 1 ,则将 \(a\) 异或上 \(p[j]\)
-
对于 \(j\in(i,BIT_{MAX}]\) ,若 \(p[j]\) 的第 \(i\) 位为 1 ,则将 \(p[j]\) 异或上 \(a\)
-
最后令 \(p[i]=a\)
针对这种方法的模板代码
(这种方法求最大值时直接所有 \(p[i]\) 异或起来即可)
应用:
查询最小值:
一般是线性基中最小的元素,若有 \(0\) ,需要特判
查询一个数 \(a\) 是否能被异或出来:
从高到低,如果 \(a\) 在第 \(i\) 位上为 1 ,则异或上 \(p[i]\) ,重复上述步骤,如果最终 \(a=0\) ,说明可以被异或出来
查询异或第 \(k\) 小
我们如果能使第 \(i\) 位的选择不会影响后面几位的选择,那么我们就可以用类似于二叉树求第 \(k\) 小,对于当前一位选或不选,就会将排名分成两半;
因此我们只能使用第二种构造线性基的方法
例题1:P4151 [WC2011]最大XOR和路径
题意:求一条 \(1\) ~ \(n\) 的路径,使得经过的边权的异或值最大;注意:多次经过同一条边的时候,需要异或上多次边权
时刻记住:一条路径可以表示为一条主路径(链)+多个环
设边 \(k\) 是连接链和环的公共边,也就是这条边会被经过两次,显然它的贡献就是零
我们就可以转换成一条链的异或和,再异或上若干个环的异或和,得到最大值
因此,我们可以通过对所有环的异或和求线性基,以某条链的异或和为初始值,求异或和的最大值
但显然,我们不可能去一一枚举链,这样会超时
实际上,我们只需要任意选一条链进行操作
感性理解,我们将这条链异或上若干个环,可以表示出图中所有链的异或和
但是,由于给出的图可能不是仙人掌,我们只跑一条路径可能无法求出所有的环
但实际上,这并不会影响
(借用一下大佬的图)
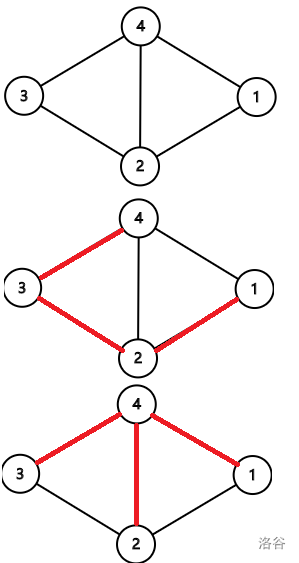
图中,第一种求法只能求出环 \(\{2,3,4\}\), \(\{1,2,3,4\}\)
第二种求法只能求出环 \(\{1,2,4\}\), \(\{2,3,4\}\)
但显然,我们将环 \(\{1,2,4\}\) 异或上 \(\{2,3,4\}\),得到的正好是 \(\{1,2,3,4\}\)
也就是说,即使不是仙人掌,但求出来的部分环可以通过相互异或得到其他的环
这对求得的线性基没有影响
因此,我们就得出此题的流程:
-
- dfs,求出一条 \(1\) ~ \(n\) 的链
-
- 在 dfs 的过程中,将遇到的环的异或和加入到线性基中
-
- 以求得的链的异或和为初始值,进行求异或值的最大值
例题2:P3292 [SCOI2016]幸运数字
题意:给出一棵树,q次询问,问一条路径上的点权异或和的最大值
我们可以考虑在每个结点 \(u\) 上保存一个线性基 \((1,u)\)
当询问到 \((u,v)\) 时,我们将 \(u\) 和 \(v\) 的线性基进行合并,合并时选择记录时对应点深度 \(>=LCA\) 的值
但我们在求 \((1,u)\) 的线性基时,\(w[u]\) 可能无法被成功加入
显然,我们要求线性基内的值对应点的深度越大越好
于是,我们考虑,当遇到 \(p[i]\not =0\) 时,如果当前位存的值对应点的深度小于 \(a\) 对应的深度,我们就将 \(p[i]\) 与 \(a\) 进行交换,再继续操作,显然这是可行的
最后用合并后的线性基求出答案即可,时间复杂度为 \(O(nloga_{max}+qlog^2a_{max})\)


