舞蹈链(Dancing Link X)
问题引入:
给出 \(n\) 行 \(m\) 列的01矩阵,现在要选某些行,求出一种方案使得每一列恰好有一个1
这是一种精确覆盖问题
DLX的原理就是:先选出 "1" 的个数最少的那一列 \(min\_num\),枚举选某一行(在 \(min\_num\) 列上有1)\(x\),然后将 \(x\) 上有 "1" 的列对应那些行全部移除,得到一个缩小的问题
其实它本质就是一个DFS的优化
来看看图,熟悉实现过程:
先选出最少 "1" 的一列:
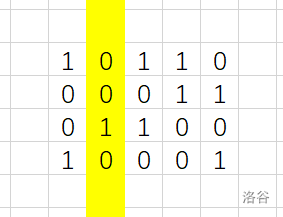
枚举行,将这一行上有 "1" 的列对应的行移除:
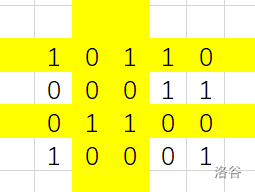
dfs下去:
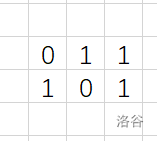
然后讲一下实现方式:十字链表
我们定义:
int L[i],R[i],U[i],D[i]; //链表元素中上下左右的信息
int x[i],y[i]; //链表元素对应01矩阵的位置
int H[i]; //十字链表中每一行的头元素
int Size[i] //每一列1的个数
我们再引入一个辅助元素 \(c[i]\),对应的是每一列头指针,即列标元素
有什么用?用处就是移除整列时我们只需要改变L[R[c]]和R[L[c]]的指向即可
不懂?看图(网上最流行的DLX图)
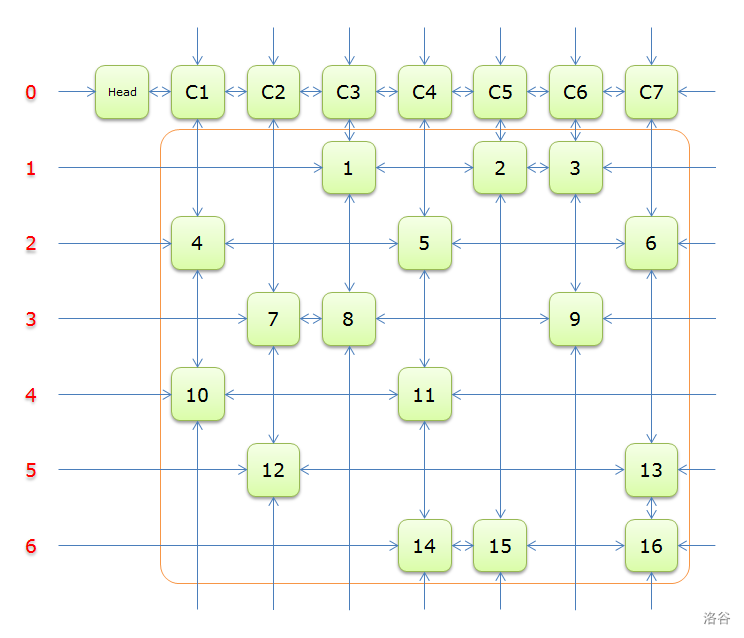
(其中实际写代码时,我们用C[0]代替head)
详细求解过程见博客园
显然,我们有可能会求解失败,那我们就要进行回溯
因为我们链表移除只是修改相邻元素的指向,自己的一点没动,所以恢复时可以用自己的信息重新接上
大概就这样,代码
理论复杂度?似乎是 \(O(\omega ^m)\),$\omega $ 是一个极其接近1的数,\(m\) 是矩阵中1的个数,也就是说,\(m\) 卡得好上万也问题不大
例题1:数独
数独有一个特点,同一行、同一列、同一宫必须出现且只能出现一次 \(1\) ~ \(9\),每一个也必须填数字,这和精准覆盖问题的定义简直完美契合
我们就可以转换为:对于 \((x,y)\) 上填数字 \(k\) 的情况(矩阵中的行),在 \((R_x,k)\),\((C_x,k)\),\((G_x,k)\),\((x,y)\)上的格子填1(括号表示矩阵中的列,\(R\) 表示行,\(C\) 表示列,\(G\) 表示宫)
不太明白?看下图
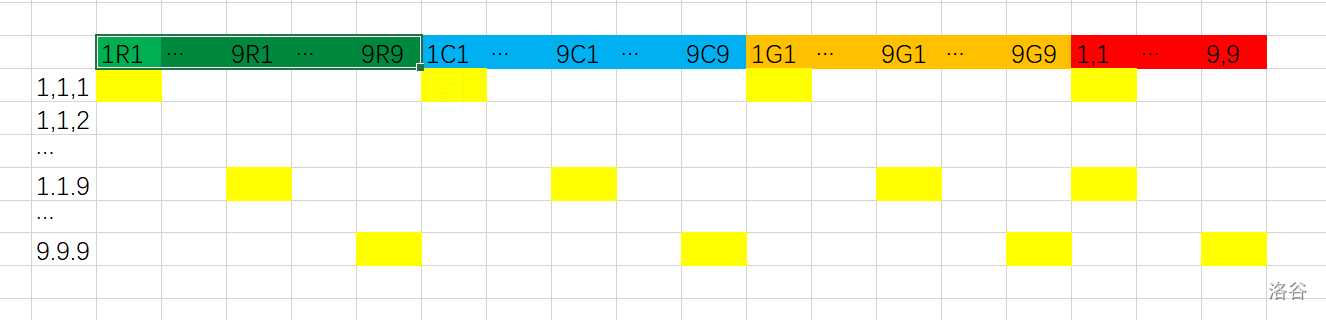
标黄的地方表示填1
然后套 DLX 就行了!
亿点点细节:
int xx=(x[i]-1)/81+1,yy=(x[i]-(xx-1)*81-1)/9+1,num=(x[i]-(xx-1)*81-(yy-1)*9);
\(i\) 表示1的编号,\(x[i]\) 才表示所在的行 \((x,y,num)\)!!!
例题2:靶形数独
这个题与上一题解法基本一样
但由于要选最大分数,所以我们要跑完所有的合法情况
恭喜你,吸氧后仍TLE俩点
那么我们就需要进一步优化:
如果一个格上已经给定了要填的数字,那么代表这一行、这一列、这一宫都不能填这个数字,且这一格也不能再填数字,那么我们就用一个bool数组进行标记,有一些01序列就可以不建。
然鹅似乎还是TLE...
我对着别人的题解对了好久,发现我的框架和题解的都是一样的
结果是我一直不会怀疑的地方有问题
就是在Resume函数和在dfs的还原中,我的链表还是向右走,也就是用 \(i=R[i]\)
当我改成 \(i=L[i]\) 后,竟然玄学地AC了...
但案例来说他们都是走一遍循环链表,理论上经过的结点是相同的
为什么会有50倍时间的差异?
而且我试着在模板题修改后再提交,确实快了不少
十分玄学,好好记着吧...
小结:
对于精确覆盖的问题:
-
先将问题转换为01矩阵
-
跑DLX
-
按题目选择:跑出一种合法解就 \(exit(0)\),或要全部解都跑完


