计算几何
前置芝士:
向量:
-
定义:既有大小,又有方向的量叫做向量(Vector)。
-
可以表示为 \(\overrightarrow{AB}\) 或 \(\vec a\)
-
由于向量平移后不变,所以也可以用 \((x,y)\) 表示向量,即将尾端平移至原点,记录头端的坐标
-
-
向量的模:\(|\overrightarrow{AB}|=\sqrt{x^2+y^2}\),即向量的长度
-
"-" 表示方向相反,即 \(\overrightarrow{AB}\) 与 \(-\overrightarrow{AB}\) 方向相反(但它们的模相等)
-
"0" 表示零向量(模为0)
- 其中,零向量与任意一个向量平行(共线)、垂直,即零向量大小为 0,但方向不定(这东西估计是数学天天考的东西,和OI关系不大)
向量的计算:
加减法:
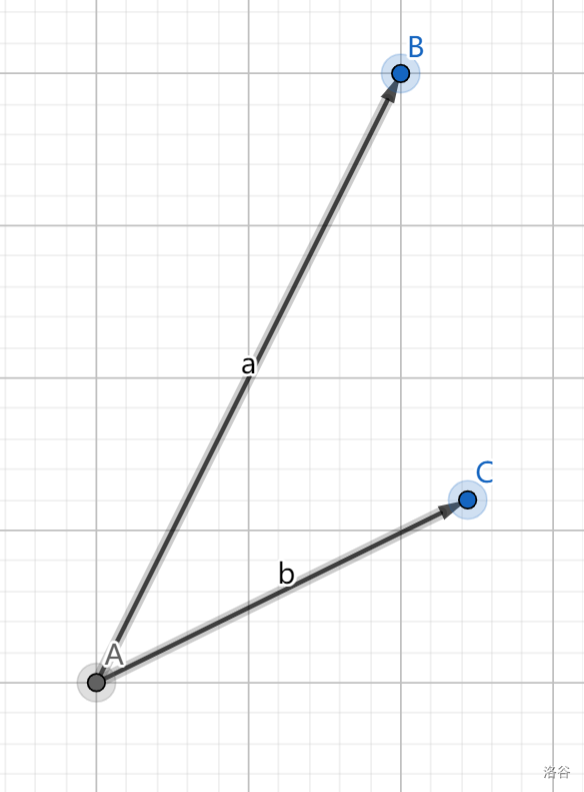

-
如图,\(\vec a+\vec b\),就是将 \(b\) 的尾端平移到 \(a\) 的头端(多项的以此类推),然后将第一条的尾端指向最后一条的头端,得到的向量就是他们的和
-
减法类似,就是 \(\vec a-\vec b=\vec a+(-\vec b)\)
-
如果用点坐标表示,若 \(A(x_1,y_1),B(x_2,y_2)\) (注:这里既可以表示一个点,也可以表示一个向量)
-
\[\overrightarrow{AB}=(x_2-x_1,y_2-y_1) \]
-
\[A+B=(x_1+x_2,y_1+y_2) \]
-
注:向量加法满足交换律、结合律
乘法:
- 数乘:
-
k个相同向量的和可以表示为向量的数积,可以表示为 \(k\vec a\) ,结合向量加法很好理解
-
注意,如果 \(k<0\),那么结果的方向与 \(\vec a\)的方向相反
- 点乘:
-
记作 \(\vec a · \vec b\)
-
定义:\(\vec a · \vec b=|\vec a||\vec b|cos \theta\)
-
由余弦定理等推到可得 \(\vec a · \vec b=x_1x_2+y_1y_2\)
-
一些应用:
-
两向量垂直:\(\vec a \perp \vec b\Leftrightarrow \vec a · \vec b=0\)
-
两向量共线:\(\vec a=\lambda \vec b \Leftrightarrow |\vec a · \vec b|=|\vec a||\vec b|\)
-
-
注:点乘满足交换律、结合律、分配律,结果为标量!
- 叉乘:
-
记作 \(\vec a\times \vec b\)
-
叉乘的计算结果是向量!方向为垂直于原来两个向量所在的平面(右手法则判断)。
-
在模的意义上为:\(|\vec a\times \vec b|=|\vec a||\vec b|sin \theta\)
-
几何意义为两向量围成的平行四边形的面积
-
\(|\vec a\times \vec b|=x_1y_2-x_2y_1\)
-
一些性质:(叉乘不满足交换律、结合律,但满足分配律)
-
\[\vec a \times \vec b=-\vec b\times \vec a \]
-
\[\vec a \times (\vec b+\vec c)=\vec a \times \vec b+\vec a \times \vec c \]
-
\[(k\vec a)\times \vec b=\vec \times (k\vec b)=k(\vec a\times \vec b) \]
-
\[\vec a \parallel \vec b\Leftrightarrow \vec a \times \vec b=0 \]
-
旋转:
逆时针旋转 \(\theta\) ,得 \((xcos\theta-ysin\theta,xsin\theta+ycos\theta)\)
证明:令向量 \(a=(x,y)\),倾角为 \(\alpha\),逆时针旋转 \(\theta\) 得到 \(b\)
-
\(l=\sqrt{x^2+y^2}\)
-
\(b=(lcos(\alpha+\theta),lsin(\alpha+\theta))\)
-
由恒等变换得 \(b=(l(cos\alpha cos\theta-sin\alpha sin\theta),l(sin\alpha cos\theta+cos\alpha sin\theta))\)
-
拆括号,得证
到这里算是刚刚入门了......
运用:
1. 求两直线的交点
给出 \(A\)、\(B\)、\(C\)、\(D\) 四个点的坐标,求直线 \(AB\) 与 \(CD\) 的交点
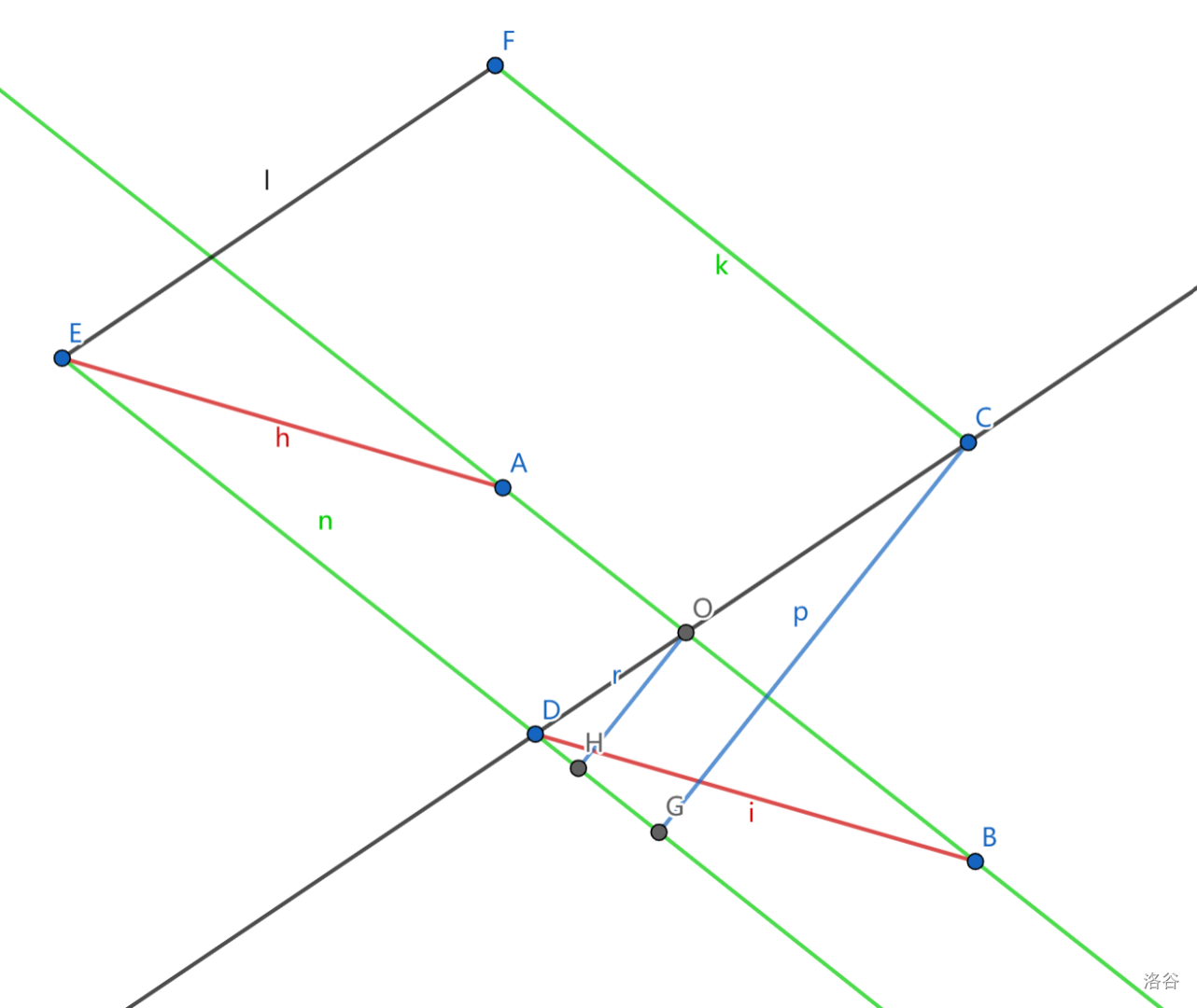
如图,如果我们将 \(AB\)、\(BD\)、\(CD\) 看成向量,那么 \(|\overrightarrow{AB}·\overrightarrow{BD}|=S_{ABDE}\),\(|\overrightarrow{AB}·\overrightarrow{CD}|=S_{CDEF}\)
因为同底,所以面积之比等于高之比,根据\(\Delta ODH\sim \Delta CDG\)又得其等于 \(OD\) 与 \(CD\) 之比:
(叉乘不具有可约性!!!)
令 \(k=\frac{|BA|\times|BD|}{|BA|\times|CD|}\)
则 \(O\) 点坐标为 \(D+k \overrightarrow{DC}\)
Point get_its(Line a,Line b)
{
double k=cross(get_vec(a.u,a.v),get_vec(a.u,b.v))/cross(get_vec(a.u,a.v),get_vec(b.u,b.v));
Point o=get_vec(b.v,b.u);
return (Point){b.v.x+k*o.x,b.v.y+k*o.y};
}
(其实话说解方程也不难求吧)
2. 判断两线段是否相交:
显然,如果两个线段相交,则任意一条线段的两点应位于另一条线段的两侧
显然,根据叉乘,我们可以快速得到两点是否在一条线段的两端:
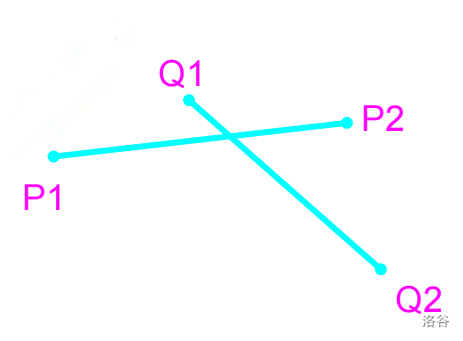
如图,如果有 \((\overrightarrow{Q_1P_1} \times \overrightarrow{Q_1Q_2})*(\overrightarrow{Q_1P_2} \times \overrightarrow{Q_1Q_2})<0\) ( \(*\) 为数乘),那么显然 \(P_1,P_2\) 位于线段 \(Q_1Q_2\) 两端
我们只需要判断两次即可
bool check_its(Seg a,Seg b)
{
double ca=cross(get_vec(a.u,b.u),get_vec(a.u,a.v))*cross(get_vec(a.u,b.v),get_vec(a.u,a.v));
double cb=cross(get_vec(b.u,a.u),get_vec(b.u,b.v))*cross(get_vec(b.u,a.v),get_vec(b.u,b.v));
return (ca<0)&&(cb<0);
}
3. 判断点 \(P\) 是否在多边形内
抛出一个显而易见的结论但不完全正确的结论:从点 \(P\) 向 \(x\) 轴正方向(即向东)做射线,如果与多边形有奇数个交点,则在多边形内
但为什么不完全正确呢?
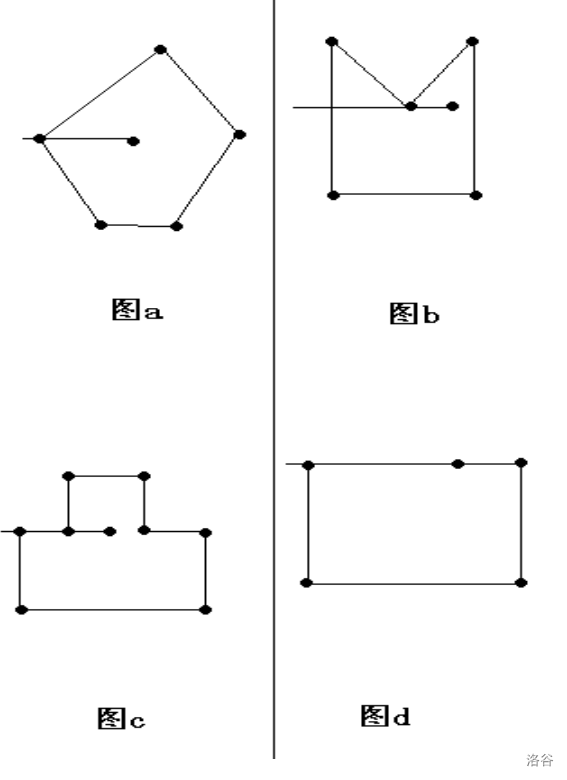
如图
那我们怎么办?
-
我们考虑枚举多边形每条边,如果有水平边,我们跳过不计
-
然后求出射线与它的交点(如果有)
-
接着,如果这个交点与这条边的端点重合,我们就约定:如果这个端点是这条边纵坐标较大的那个,我们就统计这个交点
-
这样就可以避免重复计算和凹边的干扰
也就是用 \(O(n)\) 的时间进行判断
4. 判断线段 \(AB\) 是否在多边形内
显然,我们先要判断 \(A\) 和 \(B\) 都要在多边形内
但这样还不够,因为多边形可以有凹边,所以我们还要保证线段与多边形的任意一条边不内交
- 内交:两线段相交且交点不在两线段的端点
但这样还不够,上反例:
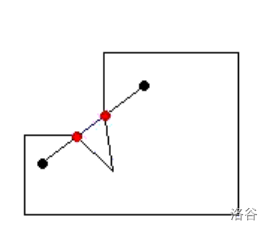
你看,它确实也没有内交啊,但它就是出去了怎么办
那我们将这些交点排序,判断相邻两个交点的中点是否也在多边形内
(但似乎这复杂度有亿点高吼)
1.二维凸包:
定义:能将平面上所有点围住的最小(周长)的凸多边形
因为他是凸的,所以有一个特别有用的性质:逆时针数,每条边都应该向左转
怎么判断?
这就用到叉乘了:因为如果一条边相对于另一条边是向左转的话,那么它们的夹角应该为正(\(0\) ~ \(\pi\)),\(sin\theta\) 也应该为正
所以只需要判断"上一条的连边"和"当前要连的边"的叉乘是否为正即可判断转向
要是向右转了,就将栈顶的点弹出,直到不右转或者只剩初始点为止
那如果点是乱的,如何实现这个想法?
Graham算法:
我们很容易发现,凸包上的点与原点连边的极角(就是任意角制)是不断增大的
那么我们就先找出一个y值最小(如果有相同那再x值最小)的点作为原点,然后按照与这个点的极角从小到大排序,然后做一遍判断,就搞定了!
注意排序的时候,如果有与原点横坐标相同的点,应该按y值从小到大排序;有极角相同的点,应该按x值从小到大排序(自己模拟几遍就应该可以理解了)
注意: G算法所得的凸包是没有最后一条边的,因此要在栈的最后加上第一个点;但下面的A算法就不会有这个问题
Andrew算法:
但我们看到G算法中,每次比较都要求两个atan,这个常数似乎挺危的
于是大佬们就在G算法的基础上进行了改进
我们又可以发现,凸包的点的横坐标都是先增大,然后再减小
那我们可不可以按照点的x值进行排序?
of course,我们可以按x值从小到大排序(x相同时按y值从小到大),然后我们先正着跑一遍判断,这样就求完凸包的下凸壳,然后再倒着跑一遍,就可以求完上凸壳
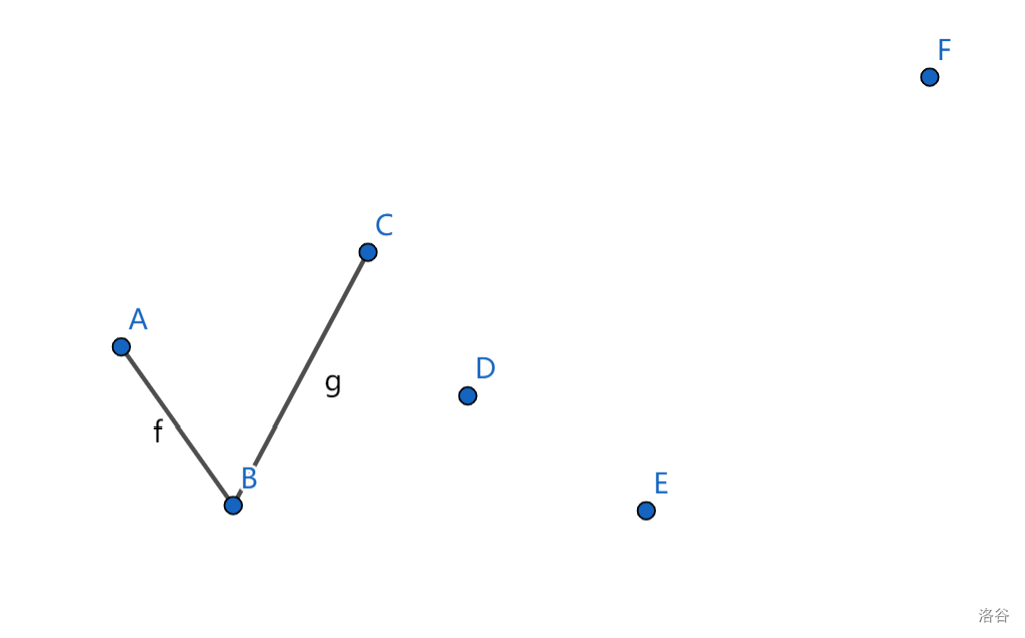
不太理解?看看下面的图:
初始状态:
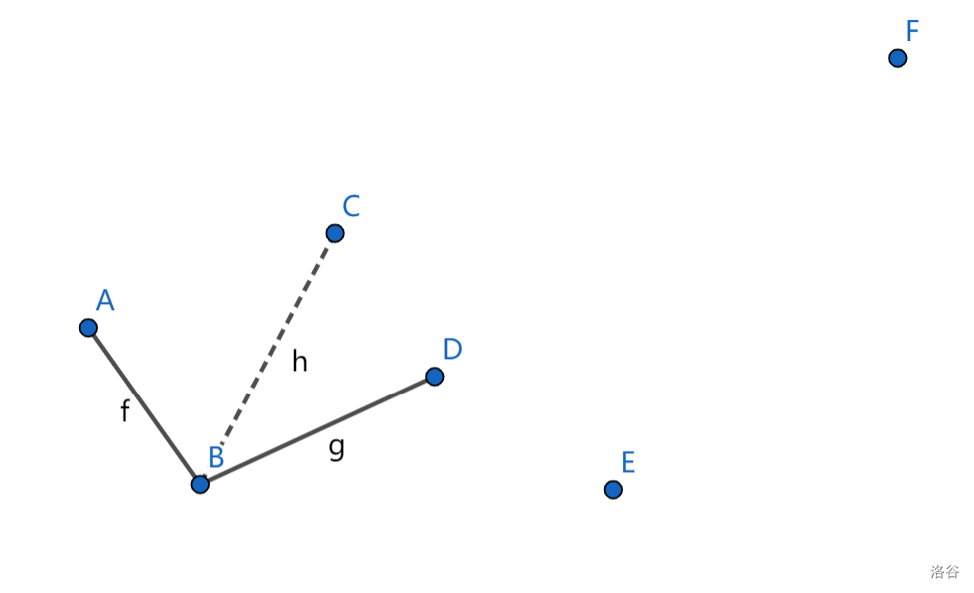
判断到D点,C点弹出:
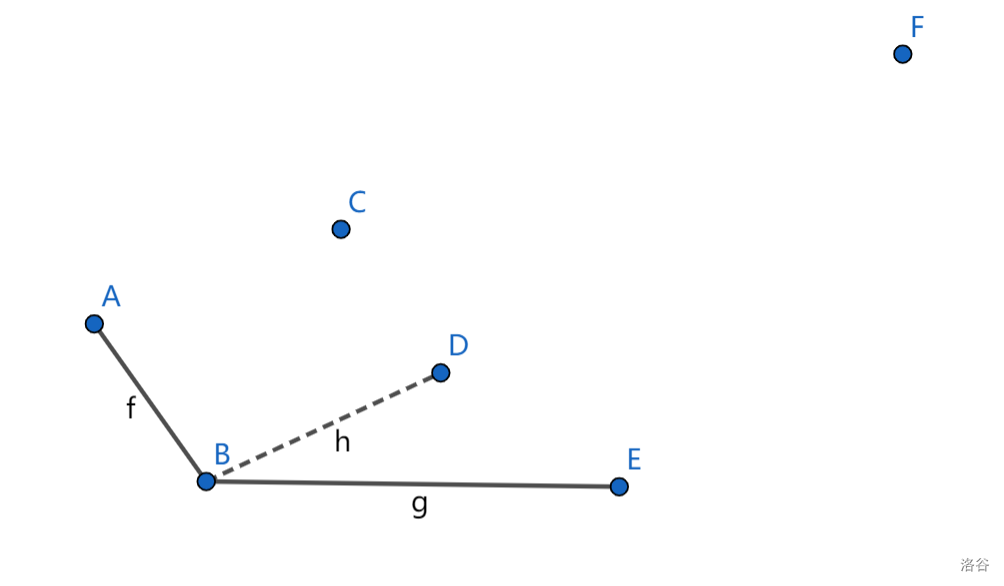
到E点,D点弹出:
最后连上F点:

然后倒着做,到D点:
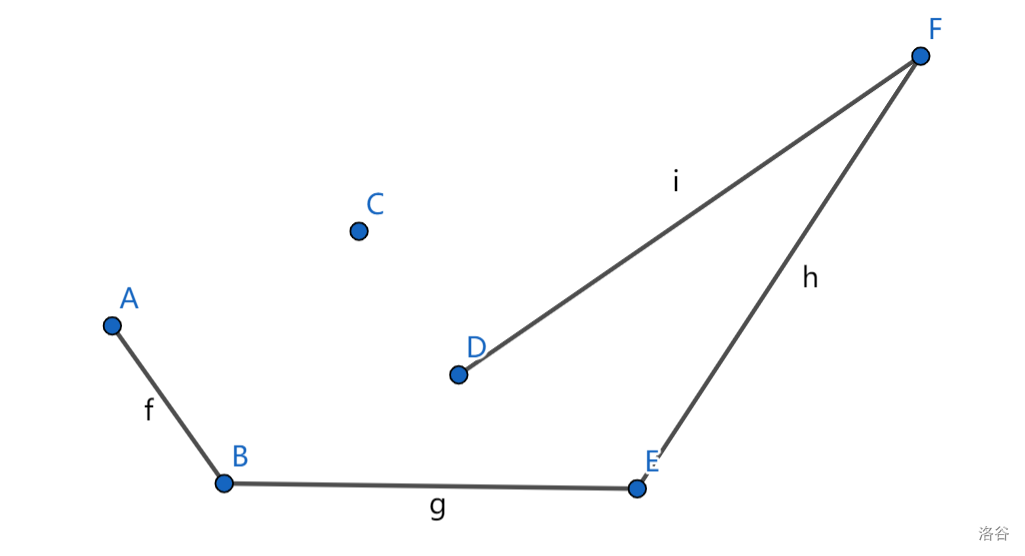
到C点,D点再弹出:
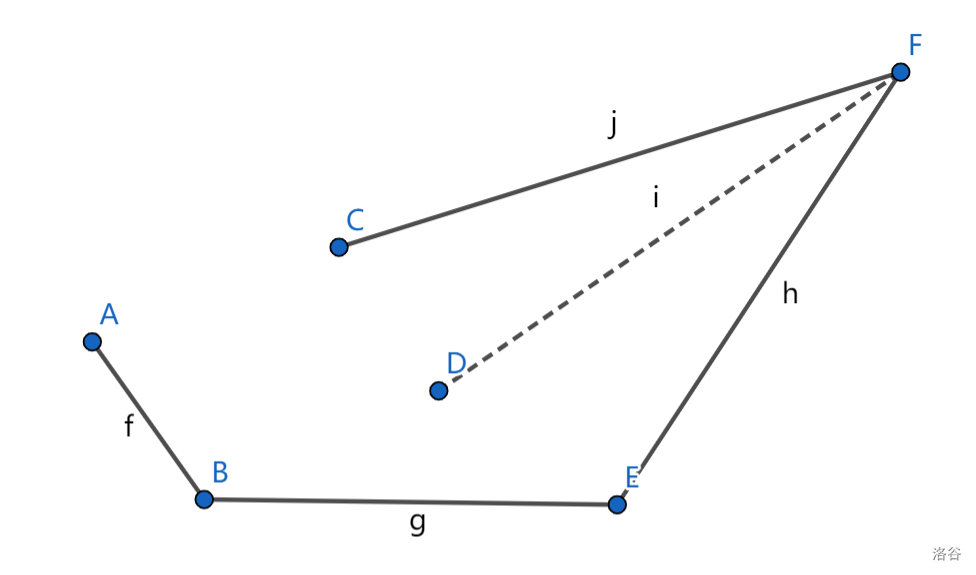
最后连回A点:
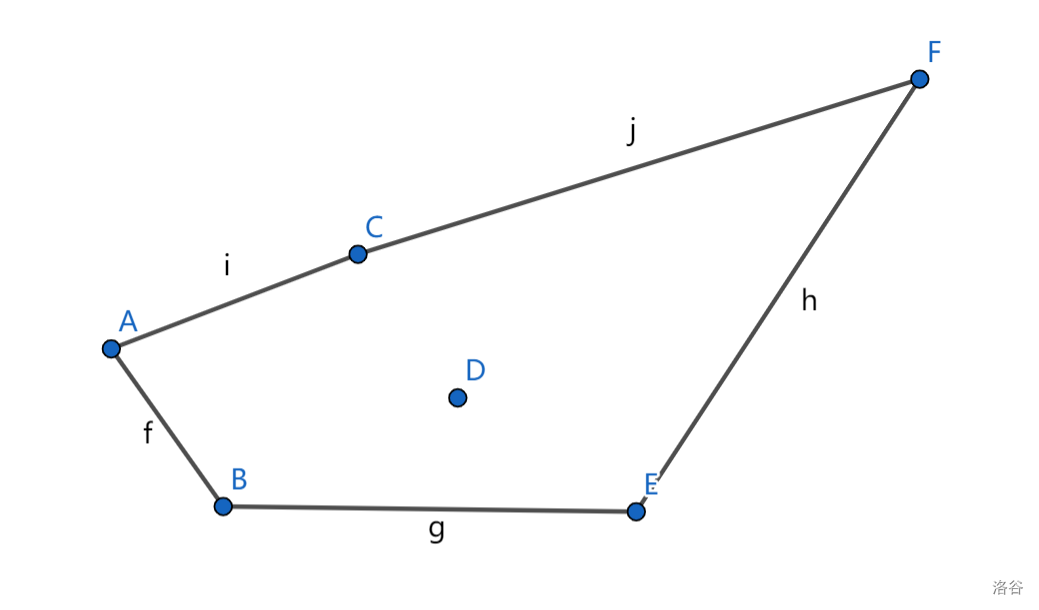
完结撒花!
但是!
注意栈要开两倍!!!(我就是因为直接从G算法上面改导致调了1个小时...)
注意: A算法在判断上一条边是否要弹出时,叉积为 0 时不能弹出!因为如果点的纵坐标全部相同时,最后就只剩下第一个点,这是它反着再做一遍的缘故
从运行时间看,G稳定在101ms左右,A在92ms左右,说明A确实更快!
但实际上,在做旋转卡壳的时候,A算法会有很多细节问题(例如点的纵坐标全部相同),因为旋转卡壳要求一条边不能拆分成多条边表示,否则可能在卡壳的时候会进入死循环......所以还是建议优先选择G算法
例题:[SHOI2012]信用卡凸包
良心SH将算法打在题目上
题意很好理解,难处理的就是那个圆弧怎么办
根据OI的直觉,我们可以将磨平的圆弧的圆心当成点,把它连起来
我们就会惊奇地发现,似乎这些线与答案中的直线部分是相平行的?
其实也很好理解:这相当于将答案的所有线向内缩一个 \(r\) 的长度
然后因为所有凸多边形的外角和都是360°,因此我们只需要最后将答案加上\(2\pi r\)即可
(这题因为我输错一个变量导致调了半个晚上都没调出来...)
求卡的四个点,我们只需要一些三角函数的知识即可
2. 旋转卡壳
基本问题为 \(O(n)\) 求凸 \(n\) 角形的对踵点
经典问题为求凸包的直径
显然,一个凸包的直径的两端一定在凸包的定点上
那么我们就有一个想法:将一对平行线绕着凸包的边和定点进行旋转,某一刻这对平行线的距离便是凸包的直径,如图:

我们考虑枚举凸包的边,并求出每条边的最远点 \(Q\)
显然,\(Q\) 的最远点是这条边的两个端点中的一个
那肯定有不少人像我一样问了,为什么不能枚举凸包的点,求点对应的最远点呢?
原因是:若我们按顺序(如逆时针)来枚举边,那么边对应的最远点一定也按这个顺序出现,但枚举点就不符合这个性质了
这样我们每次枚举下一条边时,我们就可以继承上一条边枚举到的结果,继续逆时针寻找最远点,这样时间复杂度就是 \(O(n)\) 的了
那我们怎么找边的最远点?
一种方法:计算三点的三角形面积,因为同底,所以面积越大,点到边的距离越远
三角形面积可以用叉积求出(平行四边形的一半啊)
但这题坑还是不少...
-
- 多点共线
如果不是所有点都共线还好,如果所有点都共线,那在选择卡壳时就真的卡壳了(因为求出来的面积始终为 0 )
因此我们要将共线的点化成一条线,但显然,A 算法很难做到,不然有可能最后得到的只是一个点,因此我们选择 G 算法
-
- 凸包只有两个点
这样说明我们无法进行旋转卡壳,因为旋转卡壳要求至少 3 个点,但我们也只需要特判一下即可
偷偷放一下之前查错时的 debug 数据(不公开):
data
例题:[HNOI2007]最小矩形覆盖
这道题成功又让我对自己的码力产生怀疑
我们凭直觉可得,最小矩形至少有一条边与凸包的边重合(OI 的直觉很重要的)
于是我们考虑枚举凸包的边,维护这条边对应的最左点,最右点,最高点
最高点和求直径的方法是一样的
最左点?显然也可以用旋转卡壳来求(最右点同理)
最左点我们可以转换为:点 \(A\) 到点 \(Q\) 所在的与 \(AB\) 垂直的直线的距离最大
就是下图:

显然,\(L_1 < L_2\) ,所以 \(Q_2\) 比 \(Q_1\) 更靠左
考虑到 \(L=AQ\ cos\alpha\) ,我们可以用点积来求,即 \(\overrightarrow{AB}·\overrightarrow{AQ}=|AB||AQ|cos\alpha=|AB|L\)
但因为 \(90<\alpha<180\) ,所以点积越小越靠左
最右点只需要反过来即可
但要注意:最左点的初始点应该是从:枚举的第一条边求到的最高点开始求!否则就会停在右侧导致 wa 掉
然后我们只需要求出矩形面积并比较即可
怎么求?显然是先求出枚举的边 \(AB\) 的解析式,然后左右两条边的斜率(\(k\) 值)是 \(\frac{-1}{k_{AB}}\) (垂直的性质),再代入最左、右点的坐标算出左右两条边的解析式,然后求出交点,用叉积算出矩形的面积
但有一个注意的点:如果矩形有边平行于 \(y\) 轴,那么它是算不了解析式的,所以我们要特判掉枚举的那条边的两个端点 \(x\) 或 \(y\) 值相同的情况
这道题大体就做完了,但作为省选题,怎么可能真的让你纯粹做一道模板题?于是它还卡了精度......
我们则需要将答案小于 \(eps\) 的值直接输出 \(0.00000\),否则你会发现你保留五位小数后输出的是 \(-0.00000\)
3. 最小圆覆盖
虽然它是就是凸包上套一个圆,但凸包 + 旋转卡壳并不能做......
我们先引出一个随机增量法:即将所有点在一开始的时候就打乱
这跟我们下面的操作有关
我们先假定已经求出了点 \(p[1]\) ~ \(p[i-1]\) 的最小覆盖圆 \(C(i-1)\)
现在如果增加一个点 \(p[i]\):
-
- 如果 \(i\) 在 \(C(i-1)\) 内,则\(C(i)=C(i-1)\)
-
- 如果 \(i\) 在 \(C(i-1)\) 外,显然 \(p[i]\) 应该在当前的最小覆盖圆上,我们考虑进行一下步骤:
-
① 假定当前圆 \(C'\) 的圆心为 \(p[i]\) ,半径为 \(0\)
-
② 枚举 \(j\in [1,i)\) ,如果 \(p[j]\) 在当前圆 \(C'\) 外,则说明 \(p[j]\) 也应在当前的最小覆盖圆上,令当前圆 \(C'\) 更新为:圆心为 \(p[i]\) 与 \(p[j]\) 的中点, \((p[i],p[j])\) 为圆的直径,然后进入步骤③
-
③ 枚举 \(k\in [1,j)\) ,如果 \(p[k]\) 在当前圆 \(C'\) 外,则说明 \(p[k]\) 也应在当前的最小覆盖圆上,那么 \(p[i],p[j],p[k]\) 三点确定一个圆,将当前圆 \(C'\) 更新为圆 \(C(p[i],p[j],p[k])\);枚举完后返回步骤②
这内含了第一数学归纳法的思想
写成伪代码就是这样:
圆 C
for(i = 1 to n)
if(p[i]在圆 C 外)
{
C = 圆(p[i], 0); //p[i]是圆心,0是半径
for(j = 1 to i - 1)
if(p[j]在圆 C 外)
{
C = 圆(p[i] 与 p[j] 的中点, dis(p[i],p[j]) / 2);
for(k = 1 to j - 1)
if(p[k]在圆 C 外)
C = 三点共圆(p[i], p[j], p[k]);
}
}
但数据应该是 \(1e5\) 的啊,这 \(n^3\) 不对吧?
这就是随机增量的妙处了:
由于一堆点最多只有 \(3\) 个点确定了最小覆盖圆,因此 \(n\) 个点中每个点参与确定最小覆盖圆的概率不大于 \(\frac{3}{n}\)
所以我们在当前循环进入下一个循环的概率不大于 \(\frac{3}{i}\)
设每一层循环的复杂度为 \(O_1\), \(O_2\), \(O_3\)
那么有:
一步步推,就能得到 \(O_1=O_2=O_3=O(n)\)
下面讲些求外接圆的方法:
众所周知,三角形的外心(即三条中垂线的交点)就是三角形外接圆的圆心
那么我们只需要将三角形其中两边看做矢量,进行矢量的旋转(\(90\degree\)),再用两直线求交点的方法求出即可
半径便是求出的圆心到三角形任意一点的距离
(代码中为了确保精度,半径一直以平方的形式储存,最后输出才开方)
(可恶这题还卡精度,开了 long double 才过了)
4. 半平面交
半平面:平面上直线的一侧即为半平面
半平面交:指多个半平面的交集。
常见的有求多个凸包交集的面积、一个凸包的核
这里介绍 S&I 算法:
我们先将凸包的点按逆时针连成向量,这样我们就是求所有向量的左半平面交
接着将所有边按照极角排序(类似求二维凸包 G 算法的排序),如果遇到极角相同的两条边,优先将靠左的边放在前面(因为靠右的边一定不会有贡献,方便求交时直接跳过这些平行边)
判断相同极角边的位置的方法:将一条边的起/终点分别与另一条边的起点和终点连成向量,如果这两个向量的叉积大于 0 ,说明这条边在另一条边的左边(类比一下判断两直线是否有交的比较)
接下来是求交的过程:(建议自己模拟一遍,有助于理解)
我们用一个双端队列来实现:里面存的是对半平面有贡献的边
对于新加入的一条边,我们判断队列尾、队列头在加入这条边后是否不再有贡献,如果是,就将队尾/队头的边弹出
如何判断?因为我们的边的极角是从小到大进行了排序的,那么半平面交也会逐渐向逆时针旋转,那么对于队列中相邻两条边的交点,如果它处于新加入边的右半平面,显然产生这个交点且处于队列两端的那条边就不会再有贡献了
在所有边加入完后,我们还要用队头的边检验一下队尾是否有多余的边,因为我们每加一条边,都是默认它会有贡献,但实际上它有可能对我们的半平面交根本没影响,此时我们就应该去除这些边(还可以理解为:因为这些边是一个逆时针循环,最后一条边的“下一条边”就是开始的边,我们最后的判断就相当于将开始的边再加入一次求交)
注意:我们要先弹出队尾,再弹出队头
如图,如果你先弹出队头,显然就扩大范围了
实际上 \(M\) 点是由 \(\vec u\) 和 \(\vec v\) 共同构成的,而因为我们在极角排序后,向量是逆时针顺序,所以 \(v\) 的影响要更大一些。
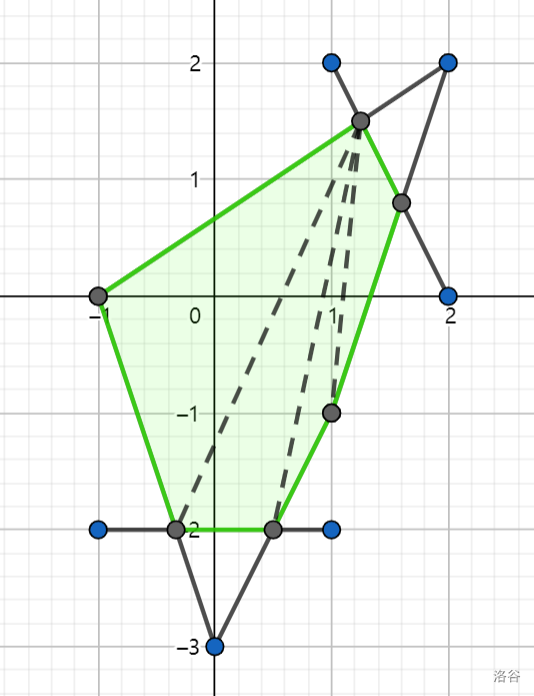
为了便于理解,我们用模板题的样例进行模拟:
先构造向量,排序,先加入前两个向量 \(a(2,2)(-1,0)\), \(b(-1,2)(-2,0)\)
加入 \(c(-1,0)(0,-3)\) ,判断后弹出 \(b\)

加入 \(d(-2,0)(-1,-2)\) ,无影响,再加入 \(e(-1,-2)(1,-2)\) ,弹出 \(d\)
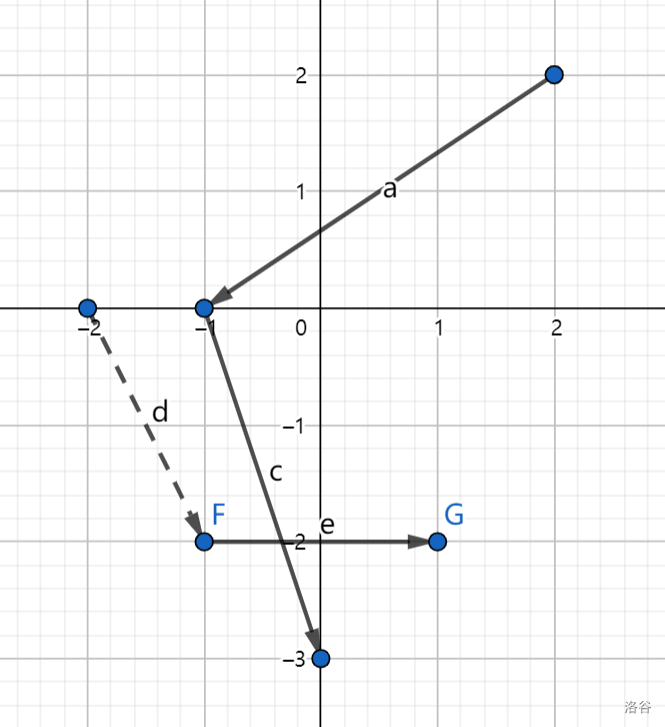
加入 \(f(-1,-2)(1,-2)\) ,无影响,再加入 \(g(1,-2)(2,0)\) ,发现与 \(f\) 共线(平行),于是弹出 \(g\)

加入 \(h(1,-1)(2,2)\) 、\(i(2,0)(1,2)\) 、\(j(1,2)(-1,2)\)

但显然,\(j\) 对我们的半平面交没有任何贡献,所以我们要用队头的边 \(a\) 将这些无用边弹出
然后我们连起相邻边交点,用三角形分割即可求出面积的大小:
5. 平面最近点对
这更像是一种分治的应用,和计算几何关系并不大(至少相比于之前的几个板块来说)
我们先将所有点按 \(x\) 为第一关键字,\(y\) 为第二关键字,从小到大进行排序
按照常规的思路,我们将当前 \([l,r]\) 的点按 \([l,mid]\) 以及 \([mid+1,r]\) 分治下去,并得到当前的最小距离 \(dis\)
考虑如何合并。我们以 点 \(p[mid]\) 为界,将所有 \(x\) 值与 \(p[mid]\) 相差小于 \(dis\) 的点加入到集合 \(B\) 中
我们将集合 \(B\) 按 \(y\) 从小到大进行排序,对于 \(B\) 中的每个点 \(p[i]\),找到对应的一个集合 \(C=\{p[j],abs(p[j].y - p[i].y) < dis\}\),并比较距离,更新答案
而我们为了避免重复计算,默认 \(p[j].y < p[i].y\) ,这样我们每次找答案就直接从 \(i\) 向前找,并且如果有 \(p[i].y -p[j].y >=dis\) 则直接退出循环
为什么是以 \(p[mid]\) 为界?因为我们合并时要找的是左区间的点与右区间的点 \(x\) 相距小于 \(dis\) 的点来更新答案(如果是相同区间的,那么显然在上一次分治中已经处理了),显然左右区间的边界是最佳选择,如果靠左或靠右了,都会导致找到的点不齐全
但这复杂度咋一看好像不对啊,每个 \(C\) 集合的大小不是都有可能是 \(len\) (区间长度)的吗
这里有一个有关的证明,证明了 \(C\) 的最大值为 \(7\) ,本人太弱只能感性理解,所以这里直接放图:
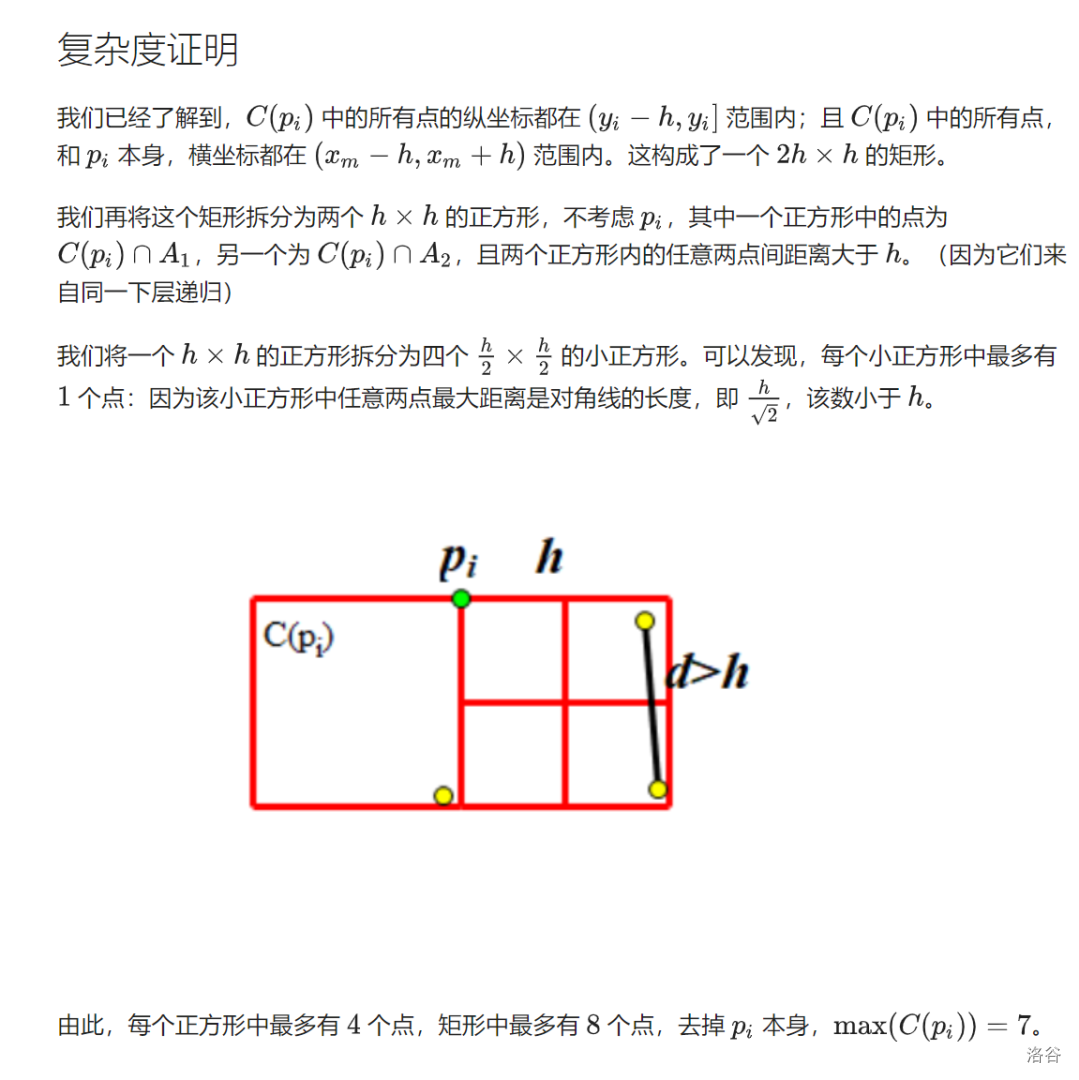
(from oi-wiki)
可能大概意思就是:当前的 \(dis\) 说明了在之前的分治中不存在距离小于 \(dis\) 的,那么在 \(\frac{h}{2}\times \frac{h}{2}\) 矩形的分布的点数最多只有一个(因为对角线都才 \(\frac{h}{\sqrt{2}} < dis\)),所以最后就不会超过 \(7\) 个点
还有一种非分治的做法,但大体思路相同,即同样按 \(x\) 为第一关键字,\(y\) 为第二关键字进行排序。每枚举一个点 \(p[i]\),便将点存入 multiset 中(set 按 \(y\) 为第一关键字,\(x\) 为第二关键字进行排序),然后枚举 set 中的元素,将 \(abs(p[i].x - p[j].x) >= dis\) 的从 set 中删除,对于 \(abs(p[i].y - p[j].y) < dis\) 的就更新答案
由于每个点最多会被插入和删除一次,所以插入和删除点的时间复杂度为 \(O(nlogn)\) ,而统计答案部分的时间复杂度证明与分治算法的时间复杂度证明方法类似



