tarjan
tarjan是指一类算法,可用来求LCA,割点/边,强联通分量。
虽然我觉得它只是dfs维护一些特殊信息罢了
1. 求LCA
利用 tarjan 可以在O(n+q)的时间内,通过1次 dfs 离线求出询问的LCA
具体实现过程:
假设 \(LCA(u,v)=k\)
那么显然,\(u\) 和 \(v\) 分别在 \(k\) 的两颗不同的子树中
dfs 中,我们一定是先遍历 \(u\) 所在的子树,再遍历 \(v\) 所在的子树,而且 \(k\) 仍在 dfs 中
那么我们就可以用并查集来得到询问的LCA
连边就在一个点 dfs 结束后,将这个点与它父节点连起来
在遍历 \(k\) 另一颗子树时,若当前结点为 \(u\),询问为\(LCA(u,v)\) ,那么我们就直接求 \(v\) 所在连通块的根即可
如果 \(v\) 还没访问到,不会出问题吗?
那在访问到 \(v\) 时,求 \(LCA(v,u)\),而此时 \(u\) 时又是访问过的,那么更新 \(ans\) 就行了
核心代码:
void dfs(int now)
{
fa[now]=now; //并查集的初始化
v[now]=true; //标记已经访问
for(int i=0;i<r[now].size();i++)
{
int to=r[now][i];
if(v[to]) continue;
dfs(to);
fa[to]=now; //更新并查集
}
for(int i=0;i<q[now].size();i++)
{
int to=q[now][i].to;
LCA[q[now].id]=finds(to);
}
}
2. 求割点
- 割点定义:对一个无向联通图,去掉某个点后,图不再联通,我们就称这个点为割点
如图:
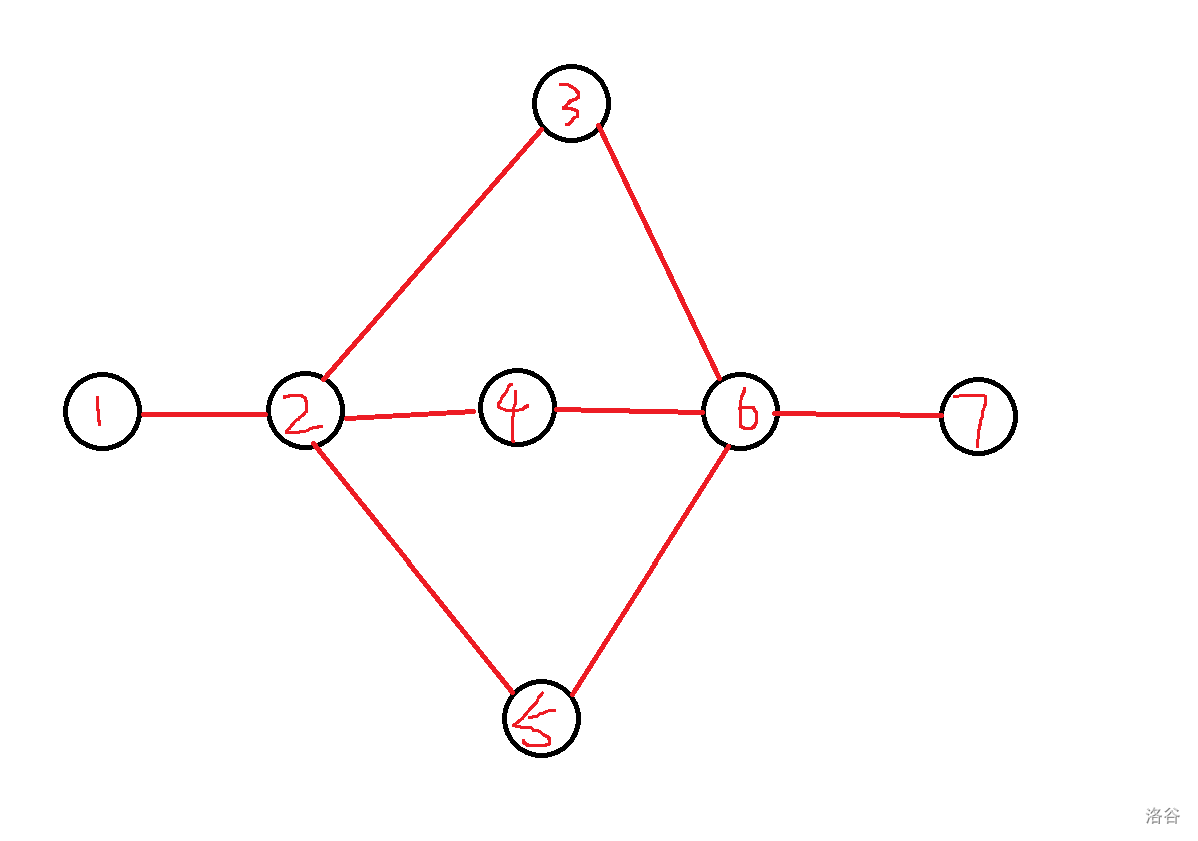
显然,点2和6就是一个割点
- 重连通图:不存在割点的无向联通图,就称为重连通图
现在我们尝试用 tarjan 来求割点
我们考虑建一棵深度优先生成树,也就是按 dfs 遍历顺序进行建树

我们来分类讨论(为什么?待会就会知道):
- 若 \(u\) 为根节点
-
显然,如果根节点有两颗及以上的子树,那它必定是割点
-
怎么判断有两个子树?如果从根节点 \(u\) 的一个子结点出发,使得所有结点都已经被访问过,那么就说明只有一棵子树;反之 \(u\) 为割点
- 若 \(u\) 不为根节点
- 稍作思考,我们就会发现,当 \(u\) 为割点的充要条件:若存在一棵子树与 \(u\) 的祖先没有回边,那么它就是一个割点
关键就是如何求第二种情况
以下是我认为 tarjan 的最精华部分:
我们定义 \(dfn[u]\) 是 dfs 的先后顺序
\(low[u]\) 表示子树中的最低深度优先数
low[u] 的计算方法如下:
\(low[u] = min\)
-
\(dfn[u]\)
-
\(low[v]\) ,\(v\) 在访问 \(u\) 前未被访问
-
\(dfn[v]\) ,\(v\) 在访问 \(u\) 前已被访问过
(其中 \(v\) 是 \(u\) 的儿子)
那么就显而易见了:若存在 \(dfn[u]<=low[v]\) ,则 \(u\) 就是割点
显而易见的是,根节点的 \(low\) 恒小于等于它所有子结点的 \(low\) ,因此我们开始要分类讨论
可能为什么能取等不太好理解,如下图:
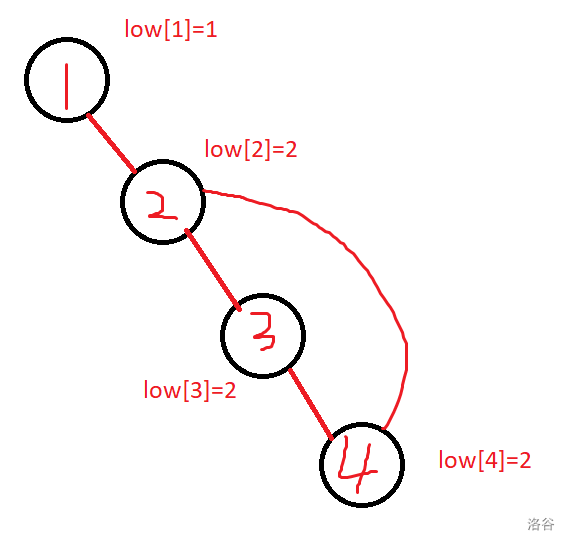
当 \(dfn[u]=low[v]\),其实就是代表将 \(u\) 点删掉后,\(u\) 的儿子会与 \(u\) 的父亲断开
两个小细节:
-
\(v\) 一定是 \(u\) 在深度优先搜索树中的子结点,才能用 \(low[v]>=dfn[u]\) 来判断 \(u\) 是割点!
-
计算 \(low\) 时,一定不能将第三点与第二点合并
(因为我开始的想法是:开始将 \(dfn[u]=low[u]=cnt\),就算遇到搜索过的结点也照样用 \(low[u]=min(low[u],low[v])\),但显然 \(low[v]\) 可能在中途已经改变,因此还是应该写 \(low[u]=min(low[u],dfn[v])\)!)
3. 求割边
割边的定义与割点类似,无非将“去掉某个点”改为“去掉某条边”,使得无向连通图不再联通
其实有了割点的经验,我们很容易联想到割边的方法与割点应该是相类似的
判断一条边是割边的充要条件就是:在深度优先搜索树中,若 \(u\) 为 \(v\) 的双亲,则要满足 \(u\) 到 \(v\) 的边没有重边,且 \(v\) 的子树中没有指向 \(u\) 和 \(u\) 的祖先的回边
因此,当 \(low[v]>dfn[u]\) 时,那么 \((u,v)\) 就是一条割边
与割点的区别就是不需要分类讨论,判断式不能取等
例题:P5058 [ZJOI2004]嗅探器
很容易看出来,我们要的答案首先它要满足是一个割点
其次,我们一定要保证这个点删掉后 \(a\) 与 \(b\) 不连通
我们考虑以 \(a\) 点为根节点跑 tarjan
对于一个割点 \(u\),如果 \(v\) 是去掉 \(u\) 后不与图联通的点,那么如果 \(b\) 在 \(v\) (注意不是 \(u\))中,那么 \(u\) 是合法割点
显然,在以 \(v\) 为根的子树中,\(v\) 的 \(dfn\) 最小
所以我们只需判断 \(dfn[v]<=dfn[b]\) 是否成立即可
4. 求强联通分量/缩点:
定义:在有向图中,若 \(u\) 与 \(v\) 可以互相到达,则称这两个点强联通;如果一个图中,任意两个点都强联通,则这个图为强联通图
显然,如果 \(dfn[u]=low[u]\),那么它就是一个强连通分量在 dfs 搜索树中的根

如图,我们可以看出,以结点 \(a\) 为根的 dfs 子树中,包含结点 \(a\) 的强连通分量,是由去掉子树中其他强连通分量剩下的点组成,因此可以递归的找出子树中所有的强连通分量
我们可以用一个栈来求强联通分量:
dfs 到某个结点 \(u\) 时,将 \(u\) 进栈。当找到 \(low[u] = dfn[u]\) (此时 \(low[u]\) 已经计算出来)的结点 \(u\) 时,代表以 \(u\) 为根的子树所有结点均已检查完毕,这个时候从栈顶到结点 u 之间所有的结点就组成一个强连通分量的点,将这些依次弹出即可
注意:当用 \(low[u] = min(low[u],dfn[v])\) 计算 \(low[u]\) 时, \(v\) 要满足的条件不只是它已经被访问过,而且 \(v\) 还得未出栈


