6.空战博弈编程实现7——将JSBSI和强化学习算法融合2024-03-24

7.博弈论与强化学习算法一 MinimaxQ, NashQ ,FFQ2022-11-20 8.博弈论与强化学习——基础1 扩展型博弈2022-11-20 9.飞机游戏二空战可视化+强化学习2022-12-07 10.gym——1自定义Gym环境并注册2022-12-07 11.博弈论与强化学习实战——CFR算法——剪刀石头布2022-12-06 12.博弈论与强化学习——— 基础2 马尔科夫博弈2022-11-20 13.飞机游戏六空战强化学习环境6.1DBML 6.1.1DBML 使用2022-12-09 14.飞机游戏五强化学习算法库2022-12-08 15.分层强化学习32022-12-08 16.飞机游戏三仿真软件 3.2Airsim介绍2022-12-08 17.强化学习与控制器2022-12-08 18.飞机游戏四飞机作战场景2022-12-08 19.飞机游戏三仿真软件 3.1JSBSim介绍2022-12-08 20.飞机游戏一飞行基础知识　１.１概念介绍2022-12-08 21.空战编程实现1——小雅2024-03-24 22.分层强化学习2024-03-24 23.问题建模2024-03-24 24.多智能体理论2024-03-24 25.马尔可夫决策理论2024-03-24 26.飞机基础知识一 1.3二维平面飞机运动学模型2023-03-25 27.飞机游戏六空战环境 6.1 DBRML 6.1.5 动作空间设置2023-03-23 28.飞行基础知识一　１.２飞机的三自由度方程2023-03-23 29.中远距空战对战场景2023-03-20 30.飞机游戏六空战强化学习环境6.1DBML 6.1.4 DBML+强化学习算法使用2023-02-14 31.飞机游戏六空战强化学习环境6.1DBML 6.1.3 DBML+强化学习算法使用2022-12-11 32.飞机游戏三仿真软件 3.3 Dogfight介绍 2022-12-10 33.飞机游戏六空战强化学习环境 6.1DBML 6.1.2源码阅读与分析2022-12-10

将JSBSim放进强化学习中

1 JSBSim模型

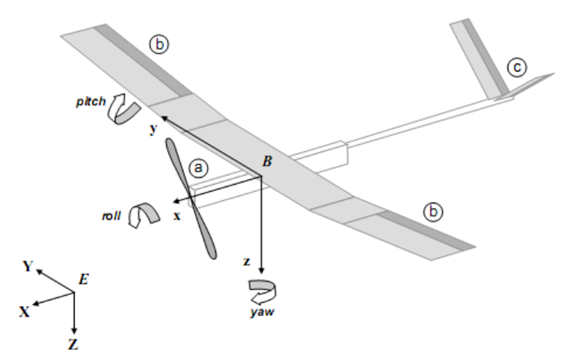
1 状态获取

位置：横轴，纵轴，竖轴坐标 $x,y,z$

fdm["position/lat-gc-deg"]  # Latitude
fdm["position/long-gc-deg"]  # Longitude
fdm["position/h-sl-ft"]  # altitude
"position/distance-from-start-mag-mt"

#使用python的Propoerty对属性进行包装

#位置
lat_geod_deg = BoundedProperty('position/lat-geod-deg', 'geocentric latitude [deg]', -90, 90) #水平位置x
lng_geoc_deg = BoundedProperty('position/long-gc-deg', 'geodesic longitude [deg]', -180, 180)#y
altitude_sl_ft = BoundedProperty('position/h-sl-ft', 'altitude above mean sea level [ft]', -1400, 85000) #高度z
dist_travel_m = Property('position/distance-from-start-mag-mt', 'distance travelled from starting position [m]') #从起始位置前进的距离

姿态：俯仰角 $\theta$ 、滚转角 $\phi$ 、偏航角 $\psi$

fdm["attitude/theta-deg"]  # pitch
fdm["attitude/phi-deg"]  # roll
fdm["attitude/psi-deg"]  # yaw
#姿态
pitch_rad = BoundedProperty('attitude/pitch-rad', 'pitch [rad]', -0.5 * math.pi, 0.5 * math.pi) #俯仰角
roll_rad = BoundedProperty('attitude/roll-rad', 'roll [rad]', -math.pi, math.pi)#滚转角
heading_deg = BoundedProperty('attitude/psi-deg', 'heading [deg]', 0, 360)#偏航角
sideslip_deg = BoundedProperty('aero/beta-deg', 'sideslip [deg]', -180, +180) #侧滑角

速度：速度 $(u,v,w)$ ，角速度 $(p,q,r)$

载体坐标系（Body Frame，符号b）
fdm["velocities/p-rad_sec"]  # The roll rotation rates 
fdm["velocities/q-rad_sec"]   # The pitch rotation rates
fdm["velocities/r-rad_sec"]   # The yaw rotation rates
#速度
u_fps = BoundedProperty('velocities/u-fps', 'body frame x-axis velocity [ft/s]', -2200, 2200) #b 载体坐标系
v_fps = BoundedProperty('velocities/v-fps', 'body frame y-axis velocity [ft/s]', -2200, 2200)
w_fps = BoundedProperty('velocities/w-fps', 'body frame z-axis velocity [ft/s]', -2200, 2200)
v_north_fps = BoundedProperty('velocities/v-north-fps', 'velocity true north [ft/s]', float('-inf'), float('+inf')) #局部导航坐标系，东北天ENU坐标系
v_east_fps = BoundedProperty('velocities/v-east-fps', 'velocity east [ft/s]', float('-inf'), float('+inf'))
v_down_fps = BoundedProperty('velocities/v-down-fps', 'velocity downwards [ft/s]', float('-inf'), float('+inf'))
altitude_rate_fps = Property('velocities/h-dot-fps', 'Rate of altitude change [ft/s]') #高度变化
#角速度
p_radps = BoundedProperty('velocities/p-rad_sec', 'roll rate [rad/s]', -2 * math.pi, 2 * math.pi)
q_radps = BoundedProperty('velocities/q-rad_sec', 'pitch rate [rad/s]', -2 * math.pi, 2 * math.pi)
r_radps = BoundedProperty('velocities/r-rad_sec', 'yaw rate [rad/s]', -2 * math.pi, 2 * math.pi)

翼弦迎角、侧滑角 $AOA,AOS$

fdm["aero/alpha-deg"]  # The angle of Attack  迎角
fdm["aero/beta-deg"]  # The angle of Slip 侧滑角

当前指令

# controls state 控制指令状态
aileron_left = BoundedProperty('fcs/left-aileron-pos-norm', 'left aileron position, normalised', -1, 1) #左副翼
aileron_right = BoundedProperty('fcs/right-aileron-pos-norm', 'right aileron position, normalised', -1, 1)#右副翼
elevator = BoundedProperty('fcs/elevator-pos-norm', 'elevator position, normalised', -1, 1)#升降副翼
rudder = BoundedProperty('fcs/rudder-pos-norm', 'rudder position, normalised', -1, 1)#尾舵
throttle = BoundedProperty('fcs/throttle-pos-norm', 'throttle position, normalised', 0, 1)#油门
gear = BoundedProperty('gear/gear-pos-norm', 'landing gear position, normalised', 0, 1)#起落架

使用 Property 和 BoundedProperty对属性进行包装

2 姿态设置

位置横轴，纵轴，竖轴坐标

fdm["ic/lat-gc-deg"] = # Latitude initial condition in degrees
fdm["ic/long-gc-deg"] =  # Longitude initial condition in degrees
fdm["ic/h-sl-ft"] =   # Height above sea level initial condition in feet

姿态：俯仰角、偏转角、翻滚角

fdm["ic/theta-deg"] =     # Pitch angle initial condition in degrees
fdm["ic/phi-deg"] =       # Roll angle initial condition in degrees
fdm["ic/psi-true-deg"] =  # Heading angle initial condition in degrees

速度

fdm["ic/ve-fps"] =  # Local frame y-axis (east) velocity initial condition in feet/second
fdm["ic/vd-fps"] =   # Local frame z-axis (down) velocity initial condition in feet/second
fdm["ic/vn-fps"] =   # Local frame x-axis (north) velocity initial condition in feet/second
        
    
fdm["ic/q-rad_sec"] = 0  # Pitch rate initial condition in radians/second
fdm["ic/p-rad_sec"] = 0  # Roll rate initial condition in radians/second
fdm["ic/r-rad_sec"] = 0  # Yaw rate initial condition in radians/second

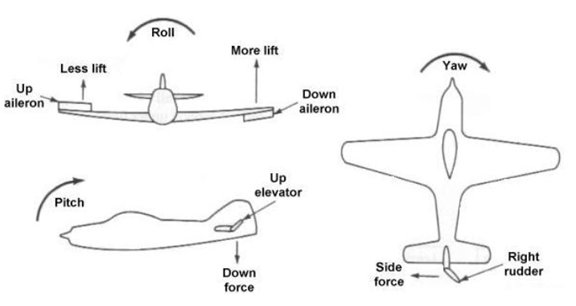
3模型的指令控制

u = [δ_{T}, δ_{a}, δ_{e}, δ_{r}]

$u = [\delta_T,\delta_a,\delta_e,\delta_r]$

where $\delta_T$ is the throttle setting and $\delta_a,\delta_e,\delta_r$ are the angular deflections of right ailerons, elevator, and rudder, respectively

# controls state 控制指令状态
aileron_left = BoundedProperty('fcs/left-aileron-pos-norm', 'left aileron position, normalised', -1, 1) #左副翼
aileron_right = BoundedProperty('fcs/right-aileron-pos-norm', 'right aileron position, normalised', -1, 1)#右副翼
elevator = BoundedProperty('fcs/elevator-pos-norm', 'elevator position, normalised', -1, 1)#升降副翼
rudder = BoundedProperty('fcs/rudder-pos-norm', 'rudder position, normalised', -1, 1)#尾舵
throttle = BoundedProperty('fcs/throttle-pos-norm', 'throttle position, normalised', 0, 1)#油门
gear = BoundedProperty('gear/gear-pos-norm', 'landing gear position, normalised', 0, 1)#起落架

$\delta_T$ the throttle setting 油门设置

fdm["propulsion/refuel"] = True  # refules the plane?
fdm["propulsion/active_engine"] = True  # starts the engine?
fdm["propulsion/set-running"] = 0  # starts the engine?
fdm["fcs/throttle-cmd-norm"]  =

$\delta_a$ ailerons 左右副翼

fdm["fcs/aileron-cmd-norm"]=
fcs_left_aileron_pos_norm=
fcs_right_aileron_pos_norm =

$\delta_e$ elevator 升降舵

fdm["fcs/elevator-cmd-norm"]=
fcs_elevator_pos_norm=

$\delta_r$ rudder 方向舵

.fdm["fcs/rudder-cmd-norm"] = 
fcs_rudder_pos_norm

状态空间

两架飞机：位置和速度和姿态信息，~~载弹量~~

S t a t e_{r e d} = [x, y, z ， θ, ϕ, ψ, u, v, w, p, q, r, A O A, A O S], S t a t e_{b l u e} = [x, y, z ， θ, ϕ, ψ, u, v, w, p, q, r, A O A, A O S] S t a t e = [S t a t e_{r e d}, S t a t e_{b l u e}]

$State_{red}= [x,y,z，\theta ,\phi,\psi, u,v,w, p,q,r , AOA,AOS], \\ State_{blue}=[x,y,z，\theta ,\phi,\psi, u,v,w, p,q,r , AOA,AOS] \\ State=[State_{red},State_{blue}]$

发射导弹之后：导弹的位置和速度,先不考虑导弹位置和速度

如果考虑导弹位置和速度，导弹的位置和速度也是环境变化中的一个量，且导弹还有自主锁敌的功能，

奖励函数设置

1 距离

距离越近越好，目的是让我方无人机主动接触敌方无人机

R e w a r d_{d i s t a n c e}

$Reward_{distance}$

基于距离的奖励设置可以分为两个部分，

一部分是根据当前情形下的实际距离给予奖励

\begin{matrix} (1) & R_{d 1} = {\begin{aligned} 5, & d < 100 \\ 4, & d < 200 \\ 3, & d < 300 \\ 2, & d < 400 \\ 1, & d < 500 \\ 0.5, & d < 800 \\ 0.2, & d < 1000 \\ 0.1, & d < 1200 \end{aligned} \end{matrix}

$\begin{equation} R_{d1}= \left\{ \begin{aligned} &5,&d<100 \\ &4,&d<200 \\ &3,&d<300 \\ &2,&d<400 \\ &1,&d<500 \\ &0.5,&d<800 \\ &0.2,&d<1000 \\ &0.1,&d<1200 \\ \end{aligned} \right. \end{equation}$

第二部分是看当前距离和上一阶段的距离是否发生了变化

\begin{matrix} (2) & R_{d 2} = {\begin{aligned} 10, & d i s t a n c e_{a g o} > d i s t a n c e_{n o w} \\ - 1, & d i s t a n c e_{a g o} < d i s t a n c e_{n o w} \end{aligned} \end{matrix}

$\begin{equation} R_{d2}= \left\{ \begin{aligned} &10,& distance_{ago} > distance_{now} \\ &-1,& distance_{ago} < distance_{now} \\ \end{aligned} \right. \end{equation}$

但文献指出当目标为动态时，两者间的距离变化不仅与智能体采取的动作相关，动态目标的位置变化也会对其产生影响; 这种情况下，即使智能体采取了远离目标的动作，其仍有可能获得正的额外奖励项。

于是其对上述奖励函数进行了改变，

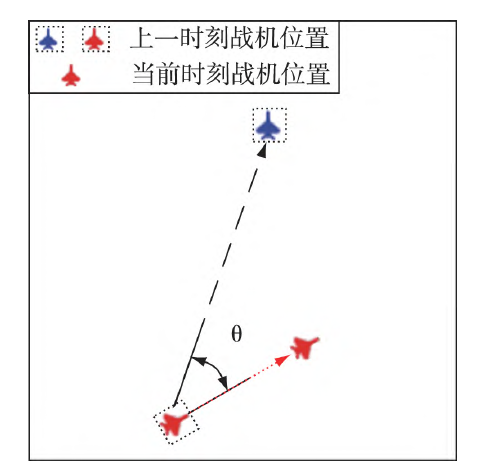
如图4 所示，以上一时刻战机和敌机的相对位置构造矢量，以上一时刻到当前时刻战机的位移构造矢量，两矢量夹角为 $θ( θ ∈［0，π］)$ ;额外奖励项 reward设置为

R_{d 2} = c o s θ * | \vec{T_{2}} |

$R_{d2}=cos \theta * |\overrightarrow{T_2}|$

此时，只有战机选择向敌机靠近的动作时，才能获得正的奖励，战机位移越大，奖励就越大。反之，当战机选择远离目标的动作时 $( θ ＞π/2)$ ，战机获得负的奖励( 即惩罚) ，其位移越大，获得的惩罚也就越大。

3 距离约束

红方和蓝方的活动范围应当被约束在正常高度的空间范围中，当超出指定范围时，应当给予惩罚

\begin{matrix} (3) & R_{d 3} = {\begin{aligned} 10, & 在指定空间范围之中 \\ - 1, & 超出指定空间范围 \end{aligned} \end{matrix}

$\begin{equation} R_{d3}= \left\{ \begin{aligned} &10,& \text{在指定空间范围之中} \\ &-1,& \text{超出指定空间范围} \\ \end{aligned} \right. \end{equation}$

代码实现

		#根据当前距离，给予奖励
        distance_plane_plane = np.linalg.norm(position_plane_blue-position_plane_red,ord=2)
        if distance_plane_plane  <self.limit_distance :
            done = True
            reward-distance1 =  50
        elif  distance_plane_plane < 100  :
            reward-distance1 = 5 
        elif distance_plane_plane < 200 :
            reward-distance1 = 4
        elif distance_plane_plane < 300 :
            reward-distance1=3 
        elif distance_plane_plane < 400 :
            reward-distance1 = 2
        elif distance_plane_plane < 500 :
            reward-distance1=1
        elif distance_plane_plane <800 :
            reward-distance1 =0.5 
        elif distance_plane_plane <1000 :
            reward-distance1 =0.2
        elif distance_plane_plane <1200 :
            reward-distance1=0.1

T_1 = [x,y,z]_blue_ago  - [x,y,z]_red_ago
T_2  = [x,y,z]_red_now -[x,y,z]_red_ago 
cosT = np.dot(T_1 ,T_2 ) / (np.linalg.norm(T_1 ) * np.linalg.norm(T_2 ) )
reward_distance2 =  cosT  *   np.linalg.norm(T_2 )

2 视角

两机形成的视角：示意图：

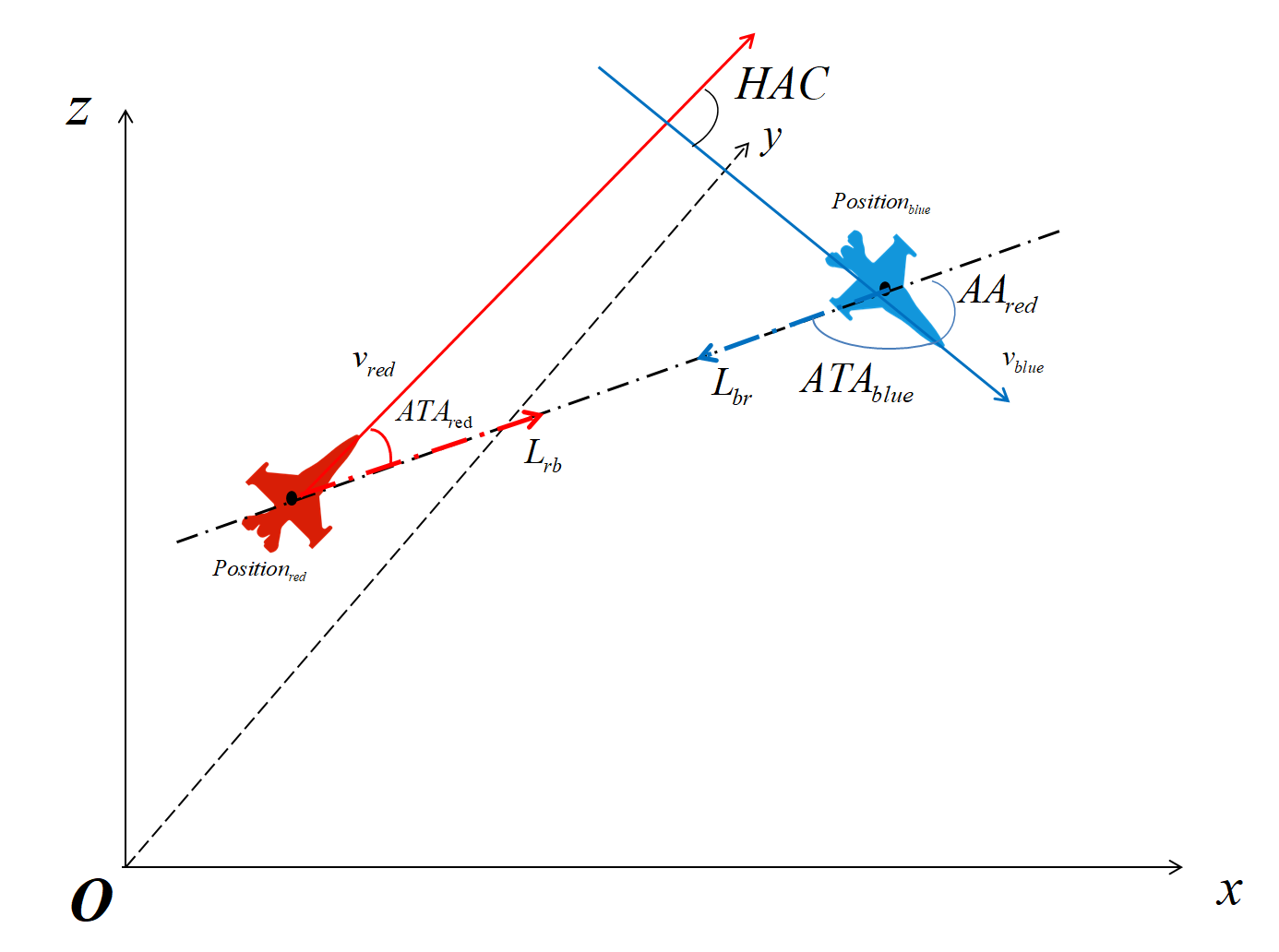
$ATA$ 为天线偏转角，也就是速度矢量与位置连线的夹角

$HAC$ 为航向交叉角，也就是两架飞机的速度矢量的夹角

$AA$ 为视界角，以红方为例，是蓝方的速度矢量方向和由红方出发的位置连线 $L_{rb}$ 的夹角

以红方无人机为例：

L_{r b} = p o s i t i o n_{b l u e} - p o s i t i o n_{r e d} c o s A T A_{r e d} = \frac{L_{r b} \cdot v_{r}}{| | L_{r b} | | \cdot | v_{r} | |} A T A_{r e d} = a r c c o s \frac{L_{r b} \cdot V_{r}}{| | L_{r b} | | \cdot | v_{r} | |}

$L_{rb} = position_{blue} - position_{red} \\ cos ATA_{red} = \frac{L_{rb} \cdot v_r}{||L_{rb}|| \cdot |v_{r}|| } \\ ATA_{red} = arccos \frac{L_{rb} \cdot V_r}{||L_{rb}|| \cdot |v_{r}|| }$

代码实现：

position_red = [x,y,z]
position_blue  = [x,y,z]
L_rb =  position_blue  -  position_red
cos_ATA_red =  np.dot(L_rb,v_red) / (np.linalg.norm(L_rb) * np.linalg.norm(v_red) ) 
ATA_red =  np.arccos(cos_ATA_red)

空战优势区

由[文献](［24］ Wang Z， Wu H L， Li H， et al. Improving maneuverstrategy in air combat by alternate freeze games with adeep reinforcement learn algorithm［J］. MathematicalProblems in Engineering，2020 （1）：1-17.)对空战优势区的定义，得到战机攻击优势区如图所示

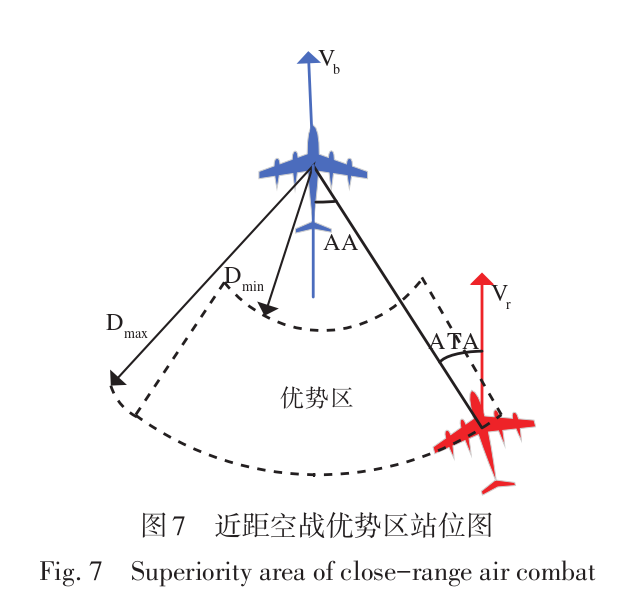
由图 7 可以看出，红方战机的$ ATA AA $越小，即蓝方战机的$ ATA $越大时，蓝方越难瞄准红方战机，红方战机就越安全，反之亦然。同时除了战机的$ ATA $和$ AA$，战机的导弹攻击区也起着至关重要的作用。

以红方为例，红方战机取得优势需同时满足以下条件：

1）红方战机的 $ATA$ 在指定的优势 $ATA$ 范围内。

2）红方战机的 $AA$ 在指定的优势 $AA$ 范围内。

3）红方战机距蓝方战机的距离 $D$ 介于最短攻击距离 $D_{min}$ 和最远攻击距离 $D_{max}$ 之间。

4）红方战机与蓝方战机的高度差 $Ｈ$ 在 $H_{min}$ 到 $Ｈ_{max}$ 范围内，该范围由战机的速度和武器攻击范围决定

当红方战机满足以上四个条件时，则判定红方战机取得攻击优势。

{\begin{cases} D_{min} < D < D_{max} \\ H_{min} ⩽ H ⩽ H_{max} \\ | A A | < {A A}_{max} \\ | A T A | < {A T A}_{max} \end{cases}

$\left\{\begin{array}{l} D_{\min }<D<D_{\max } \\ H_{\min } \leqslant H \leqslant H_{\max } \\ |\mathrm{AA}|<\mathrm{AA}_{\max } \\ |\mathrm{ATA}|<\mathrm{ATA}_{\max } \end{array}\right.$

当解决近距空战机动决策问题，因此当红方战机取得优势时，默认蓝方战机被消灭。

R e w a r d_{a n g l e}

$Reward_{angle}$

\begin{matrix} (4) & R_{a} = {\begin{aligned} 100, & 红方获得攻击优势 \\ - 100, & 蓝方获得攻击优势 \end{aligned} \end{matrix}

$\begin{equation} R_{a}= \left\{ \begin{aligned} &100,& \text{红方获得攻击优势}\\ &-100,& \text{蓝方获得攻击优势} \\ \end{aligned} \right. \end{equation}$

3 速度

具有速度优势的一方更具有作战优势，强机动性能无论是在攻击防御还是支援过程中都能发挥巨大的作用。定义速度回报函数为：

\begin{matrix} (5) & R_{v} = {\begin{array}{cc} r_{v 1} & v_{r} < 0.6 v_{b} \\ r_{v 2} + v_{r} / v_{b} & 0.6 v_{b} \leq v_{r} \leq 1.5 v_{b} \\ r_{v 3} & v_{r} > 1.5 v_{b} \end{array} \end{matrix}

$\begin{equation} R_{v}=\left\{\begin{array}{cc} r_{v 1} & v_{r}<0.6 v_{b} \\ r_{v 2}+v_{r} / v_{b} & 0.6 v_{b} \leq v_{r} \leq 1.5 v_{b} \\ r_{v 3} & v_{r}>1.5 v_{b} \end{array}\right. \end{equation}$

其中， $v_r,v_b$ 分别表示红机和蓝机的速度；

4 高度

载机的高度对导弹射程有着不可忽视的影响。高度回报函数定义为：

\begin{matrix} (6) & R_{h} = {\begin{array}{cc} r_{h 1} & Δ h < - 100 \\ Δ h / 100 & - 100 \leq Δ h < 100 \\ r_{h 3} & Δ h \geq 100 \end{array} \end{matrix}

$\begin{equation} R_{h}=\left\{\begin{array}{cc} r_{h 1} & \Delta h<-100 \\ \Delta h / 100 & -100 \leq \Delta h<100 \\ r_{h 3} & \Delta h \geq 100 \end{array}\right. \end{equation}$

其中， $h$ ——表示调节参数； ——表示高度可调参数。

总的奖励函数

连续回报函数

由距离回报函数Rg、高度回报函数R,、速度回报函数R,和角度回报函数R。利用综合指数法，有:

项目组织架构

posted @ 2024-03-24 18:48 英飞阅读(908) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 空战博弈编程实现——gym+jsbsim

· 空战编程实现1——小雅

· 数学建模学习

· Python-深度学习（三）

· Online Anomalous Subtrajectory Detection onRoad Networks with Deep Reinforcement Learning （一）

阅读排行：
· 震惊！C++程序真的从main开始吗？99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码？零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾（3.3-3.9）
· winform 绘制太阳，地球，月球运作规律

历史上的今天：
2023-03-24 Docker 挖坑

公告

昵称：英飞
园龄： 5年
粉丝： 65
关注： 2

+加关注

2025年3月

日

一

二

三

四

五

六

英飞

卧龙岗闲散人

空战博弈编程实现7——将JSBSI和强化学习算法融合

将JSBSim放进强化学习中

1 JSBSim模型

1 状态获取

2 姿态设置

3模型的指令控制

状态空间

奖励函数设置

1 距离

2 视角

空战优势区

3 速度

4 高度

总的奖励函数

项目组织架构

公告

搜索

常用链接

最新随笔

我的标签

积分与排名

合集 (2)

随笔分类 (258)

随笔档案 (124)

阅读排行榜

评论排行榜

推荐排行榜

最新评论