马尔可夫决策理论
马尔可夫决策理论
马尔可夫性( 无后效性)
某阶段的状态一旦确定则此后过程的演变不再受此前各状态的影响。也就是说“未来与过去无关”当前的状态是此前历史的一个完整总结,此前的历史只能通过当前的状态去影响过程未来的演变。
把握“当前的状态是此前历史的一个完整总结”这一要点后很多过程可以被转化描述为马尔可夫过程。当然前提是可以做到当前状态完整总结历史这点。
决策信息
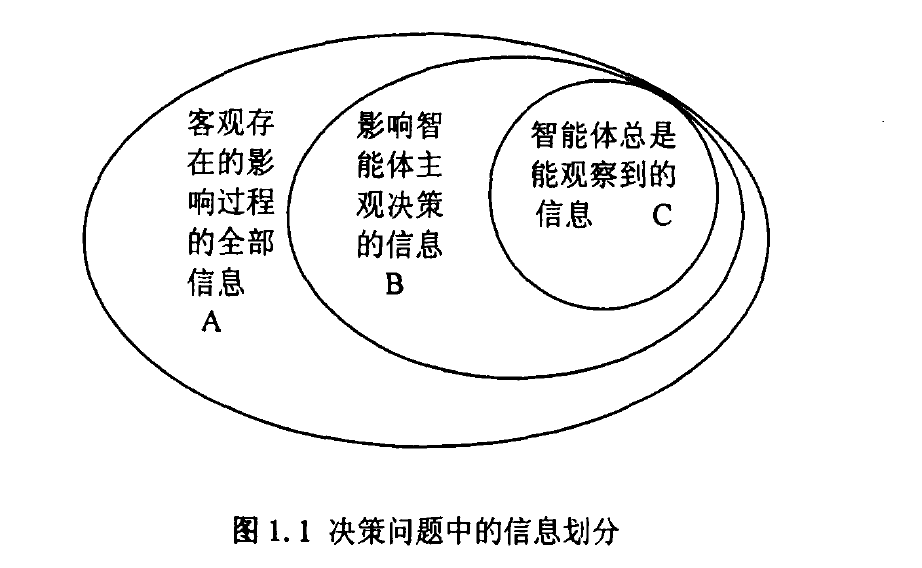
A集合:为客观存在的影响过程的全部信息,是整个客观世界的世界状态中与问题所对应过程相关的因素。
理想模型
B集合:为影响智能体主观决策的信息,进一步解释,是智能体主观上知道存在,并能够把握运用的一些信息。
因为对于某些因素,即便智能体知道应该与过程相关,但无法把握运用,这些信息也不会影响智能体决策。
比如,一般都认为掷硬币,正反面的概率各50%。事实上,风力,掷硬币的具体操作方式,抛出轨迹,用力情况,地面情况等都会影响过程结果,而这些因素通常无法把握运用,即使考虑进来,也难以改变决策。因此,这类智能体知道存在却无法把握利用的信息,及主观上根本不知道其存在而客观上却影响过程的因素,构成了B集合A集合的差别。
同时,也正是这些差别,造成了不确定性的存在。从另一个角度,只要B不是空集,基于应用的需求,就存在进行决策的意义。
但对不确定性仍需进行刻画,于是便引入了统计意义上概率。
环境 State
C集合:为智能体总是能观察到的信息。现实中很多决策过程,对于B集合中的信息,智能体有时观察不到。比如踢足球,自己身后球员的位置是会影响决策的,但却可能会观察不到。
观察 Observation
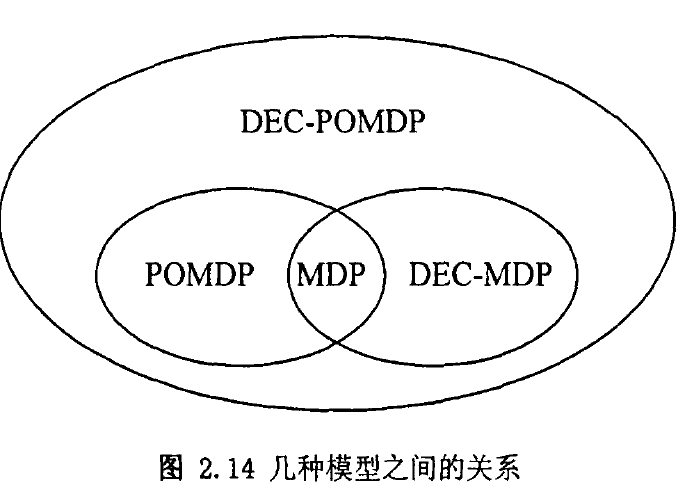
马尔可夫决策过程MDP与下面将提到部分可观察马尔可夫决策过程POMDP的区别
根据定义内容,首先有前提A>=B>=C,进而可以对问题做下面的分类:
1>当A=B=C时是一个确定性问题。
2>当A>=B=C时是一个MDP问题。
3>当A>=B>C时是一个POMDP问题。
MDP及POMDP模型中都认为决策的智能体只有一个,并把其它一切因素都归于客观环境。这些因素一部分是确定性的知识;另一部分则是己归入统计概率的不确定性。
如果认为其他智能体策略已知,论是确定性的策略亦或含概率表示的不确定性策略,那么其他智能体一样可以入环境,仍可使用MDP或POMDP模型处理。
否则,其它智能体会采用何种策略也是需要纳入考虑的,在生成智能体自身决策的同时,也要生成其他智能体的决策,这是其客观过程本身的模型决定的。分布式马尔可夫决策过程(DEC-MDP)及分布式部分可观察马尔可夫决策过程(DEC-POMDP)可以处理这类智能体合作问题。
在现实立用中,多智能体间除了合作也可能存在对抗,这类问题可以归为博弈。其中本质的区别即智能体间收益评价的不同。合作类问题,各个智能体有相同的收益评价,或者说有共同的目标;而博弈类问题,各个智能体收益评价存在区别,甚至完全对立。部分可观察的随机博弈(POSG)便是进一步扩 展的一个决策模型,可以处理这类带有不确定性的博弈问题。
半马尔可夫过程又可以称为非时齐马尔可夫过程,这是相对于一般的时齐马尔可夫过程而言的。所谓时齐是指过程的每两个相邻状态点间的时间间隔是一致的,对应决策过程则是每步行动的执行时间是定长的。非时齐则是描述了一类更一般的情况, 对应决策过程中行动的执行时间并不固定,甚至是时间上的一个概率分布。
问题特点
◆多智能体(multi-agent)
由于队友的存在涉及到合作。
由于对手的存在涉及到博弈。
◆大量不确 定因素(uncertainty)
行动结果不确定。
环境部分可观察且存在噪声。
队友之间信息不一-致。
对手模型不确定。
◆实时系统(real-time)
在每个极短的仿真离散周期内需要作出决策,实际- -般为100ms.
MDP模型
马尔可夫决策过程适用的系统有三大特点一是状态转移的无后效性二是状态转移可以有不确定性三是智能体所处的每步状态完全可以观察。
POMDP模型
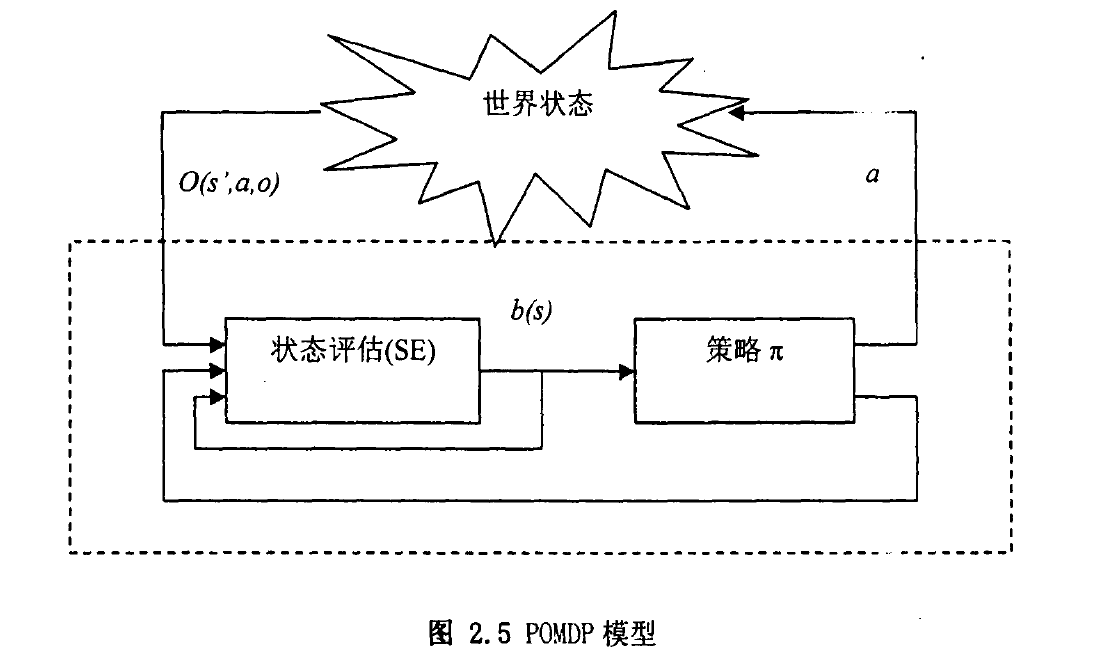
一般情况下,模型为一个六元组。其中与MDP型相同,而增加的部分为:
◆为智能体可观察信息的集合;
为观察函数,给出在执行行动并进入下一个状态时可能观察的概率分布,使用表示。
◆B: 智能体的信念状态空间,使用来描述在智能体信念中,当前处在状态的概率。
它与MDP的区别在于它建模了观察的不确定性并在模型中引入了信念状态这一个概念,是一个更一般化的模型,因而具有更广泛的应用。
观察
我们假设一个有限的观察集合我们假设一个有限的观察集合。
信念状态
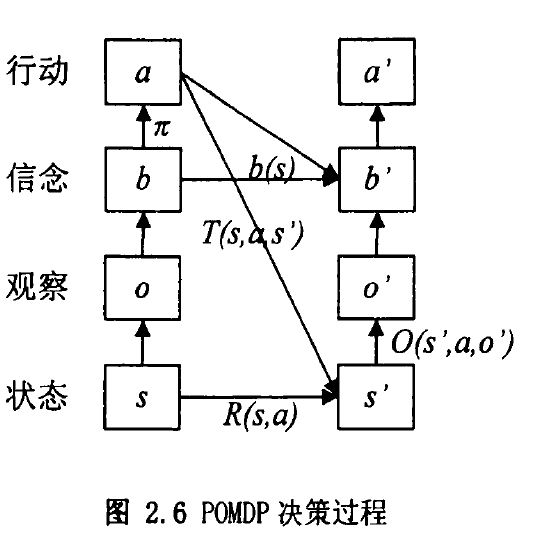
由于智能体在POMDP中不能保证每步都获得全部的当前状态信息,为了仍保持过程的马尔可夫性,这里引入了信念状态这一概念。信念状态是智能体根据观察及历史信息计算得到的一个当前状态对所有世界状态的-一个概率分布,记为,有对,有,且 。由于它是智能体主观信念上所认为的一个状态,故称为信念状态。作为一个概率分布,信念状态空间是连续的,无限的。
主观贝叶斯更新
在POMDP中,每一步的信念状态都是智能体的一个主观概率,而获得新的观察后,计算新的信念状态便可以使用贝叶斯公式进行更新。具体过程如下:
策略表示形式
在POMDP问题中,智能体通常不知道环境明确的状态,而只知道一个在所有状态上的概率分布。MDP问题中策略可以用状态到行动的映射来表示,但面对连续的信念状态空间,这一方法不再可行。
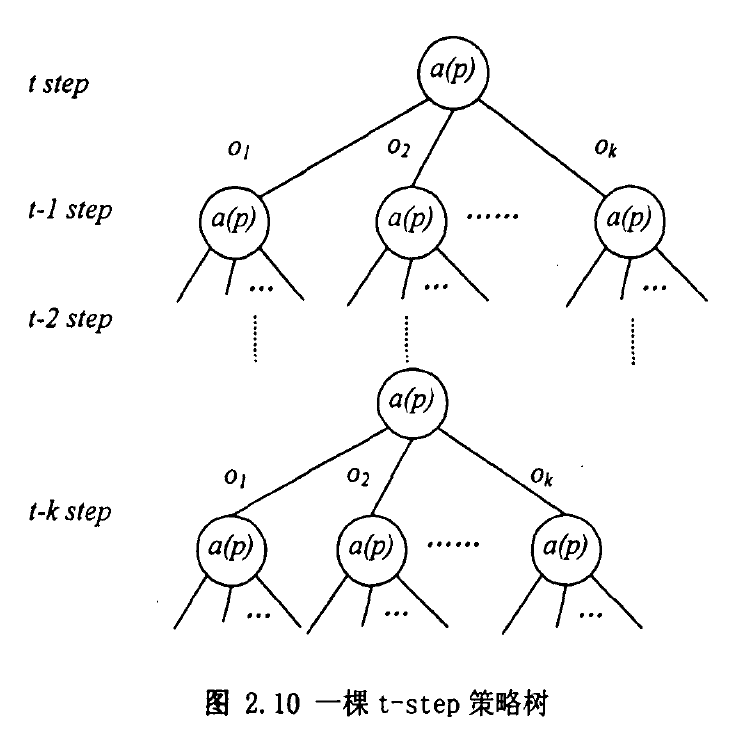
一般情况下,在POMDP问题中,智能体的t步非平稳策略可以用策略树来表示。根节点决定要采取的第一个动作,然后根据得到的观察,通过一条弧指向下一节点,这个节点在决定下一步的动作,如图2.10所示即是一-个t步策略树。在根节点处,我们有。
典型算法
值迭代算法
POMDP问题求解的两大难点,一是维度灾难(curse of dimensionality)-二历史灾难(curse of history)。前者由POMDP信念状态空间的维度等于所有可能的状态数造成,后者则是由于信念状态本质上是基于贝叶斯公式对历史的进行了一个总结,之所以有维度灾难,也是跟历史相关的。从通常的情况来考虑,比如智能体从一个确定的初始状态开始,随着观察的不确定性,信念状态所表示的对应信念空间中概率分布将在越来越多的地方取到非零值。
搜索类算法
分布式部分可观察决策过程DEC-POMDP
近年来,在人工智能领域,研究者开始对多智能体经由分布式的计算而合作达成共同目标的问题产生出越来越浓厚的兴趣(Bernstein D S, 2000)。 在这类问题中,智能体之间通常并不一定拥有良好的通讯,或者充足的带宽来达到一*种信息的完全共享。智能体之间不清楚其他合作者所观察到信息。换句话说,在同一个环境中的不同的智能体可能认为自身处于不同的状态(信念状态)。因而,相对单一智能体或者集中式控制信息完全共享的多智能合作问题,这种信息的不一致为决策增加了新的困难。
一个由;
n个智能体参与的DEC-POMDP问题定义为一个六元组,其中:
◆是一个有限的智能体索引序号
◆$S A_ii\vec{A}= \times_{i \in I}A_i\vec{a}=(a_1,\cdots,a,)O\vec{O}= \times_{i \in I}O_i\vec{a}=(o_1,\cdots,o_n)P$ 是一个马尔可夫状态转移及观察的概率分布函数,记表示在状态执行联合行动后进入状态并获得联合观察的概率。
◆为收益函数。
部分可观察随机博弈模型POSG
POSG与DEC-POMDP的区别主要在于收益函数方面,POSG中各个智能体可以有不同的收益评价方式。然而,这一点区别却将问题与博弈论(Game)联系在一-起。从一定意义上来讲,DEC-POMDP又可以看作是POSG的特例。
初始的状态分布(在某些DEC-POMDP问题中一样会给定)。POSG与DEC-POMDP的区别主要在于收益函数方面,POSG中各个智能体可以有不同的收益评价方式。然而,这一点区别却将问题与博弈论(Game)联系在-起。从一定意义上来讲,DEC-POMDP又可以看作是POSG的特例。
一个POSG问题对应了一个有限或无限步的过程,过程的深度也称为视野(horizon)。
无限视野的问题,对应的是一个平稳策略,即策略与时刻无关;有限视野的问题,对应非平稳策略。
举例而言,在一场足球赛中,刚开场时大可认为是一个无限视野问题,球员不会在意场上时间,而执行一个平稳策略;但当比赛已经进入尾声甚至是商停补时阶段,队员就可能会随着越来越接近比赛终止,使用一些不同的战术配合,即采用了非平稳策略。在POSG问题整个过程的每步之中,所有的智能体各自选择行动并获得随之而来的收益及新的观察,目标均为使期望收益最大。而智能体之间是竞争还是合作的关系,完全取决于收益函数。
相对于MDP以及POMDP问题,信息不完全情况下的多智能体问题的策略描述形式有所变化。
首先,基于信念状态来做到对历史完整总结变的不再可行。像将无限反射。因而,在信息不确定且不能完全共享的多智能体分布式决策问题中,使用类似POMDP中信念状态到行动映射的方式已无法描述策略。
除此之外,涉及博弈问题还会牵扯到纳什均衡,纯策略,混合策略等概念(OsbormeMJ,2003)。所谓纯策略是指给定一个状态则对应一个行动的确定的映射。而混合策略是映射到策略空间的一个概率分布。
在POSG类问题中,现有算法通常都是将本地策略表示成策略树的形式,比如,可以记为本地历史观察到行动的映射。在给定问题初始状态的情况下,各个智能体获得观察的组合总是有限的,这给出一种可行的策略表示方式。
多智能体系统典型决策算法
DEC-POMDP做为集中式POMDP模型的扩展被证明具有双指数的时间复杂度(Bernstein et al, 2000)。甚至只有两个智能体的有限视野的DEC-POMDP也是一个NEXP-complete问题。
基本上,目前针对DEC-POMDP问题的最优及近似最优的求解算法都完全存在于理论研究阶段,只能处理一-些规模很小的实验问题。
基于动态规划求解POSG
标准型博弈(normal form game)模型
一个标准型博弈(normal form game)模型记为,
其中是一个有限的智能体的集合。
是对智能体i有效的一个有限策略集合,
是智能体的值函数(在博弈论中又称payoff)。
不同于随机博弈过程,这个模型中没有状态及状态转移。每个策略都是一个纯策略。
令表示一个混合策略,即在对智能体i有效的全部纯策略上的一个概率分布,定义表示对应的概率。
令表示对除i外所有其他智能体的一个纯策路的剖面,同样令为混合策略的剖面。
由于智能体同时的选择策略,也可以表示智能体关于其他其他智能体可能选择策略的一个信念。若定义:
并定义智能体最佳响应函数
是一个集合的形式,其中的策略能够使得在相应的信念剖面下值函数取到最大。任何对-些信念不是最优的响应都可以删除。使用线性规划(LP)可以识别那些被支配的策略,使用下式检验-一个概率分布σ,是否超越其它策略:
检查支配的方式同POMDP算法中基本--样,但区别在于这里使用严格不等,也称为严格支配。
此外,与POMDP相比,这里还有几处不同第一,信念的不同。在一个标准型博弈中,信念指的是其他智能体的策略,而POMDP中表示潜在的状态。
第二,当存在多个智能体时被支配策略的消除方式是反复迭代的。一一个智能体消除了他的被支配策略,其他智能体的最佳响应函数可能会受到影响(假设拥有共同的理性知识)。当所有智能体做过一轮被支配策略的消除后,他们可以只考虑消除对那些刚刚被消除过的策略来说是最佳响应的额外策略。这个过程轮换,直至没有智能体再能消除其他策略,被称为被支配策略的迭代消除。对于求解标准型博弈,迭代消除法在一定程度上来说是一个弱解决方案。因为它通常并不能识别出特定的策略供智能体执行,而是提供出一系列可能的方案。
如果要选择特定的策略还需要额外的推理,这将会引入纳什均衡的概念。纳什均衡也是一个策略(有可能是混合策略)剖面,如对所有智能体有 。由于常常会存在多个均衡解,均衡选择在这里也是一个重要的问题(合作类问题的求解相对普通和博弈简单很多)。
含隐式状态的标准型博弈
模型记为,
其中是一个有限的智能体的集合
为有限状态的集合。
是对智能体i有效的一个有限策略集合,
是智能体的值函数(在博弈论中又称payoff)。
POSG中每个智能体收到的回报是一个博弈中状态及所有智能体联合策略的函数,该定义与此类似。同时它和标准形博弈一样不含有状态转移模型,取而代之的是一步行动以及收益,回报函数指定了策略的收益值 因而 它整体上是一个条件式规划。
在一个含有隐式状态的标准型博弈中,信念的定义是POMDP中信念状态与标准型博弈迭代消除被支配策略中的信念(其他智能体可能策略上的分布)的一个综合。对每个智能体定义信念为上的一个分布,记为。信念的值函数定义为:
如果对智能体i,消去一个策略d,不会降低任何信念处的值,则称d,被极弱支配。对极弱策略的检测可以使用线性规划,判断是否存在-一个混合策略满足:
在上述模型中没有包含初始状态,这和POMDP中DP类算法--直,计算直接针对所有可能的初始状态,而实际使用时,给定初始状态,也可以很快计算得到对应的策略。另外,关于值函数,在标准型博弈中,对任何一个策略剖面,都会关联-个标量值,而此处则是一一个维的向量。当给定初始状态的概率分布后,便可计算得到对应的标量值。
多智能体动态规划操作
多智能体动态规划操作与POMDP的情况类似,可以分为两步:第一步为backup操作,创建新的策略树以及向量;第二步为裁剪操作。
在backup的步骤,DP操作要求对每个智能体给定--个深度为的策略树的集合,及相应的维度为的值向量。基于行动转移,观察,以及POSG的回报模型,对每个树的集合,执行穷举backup,为每个智能体i构建出新的,同时也递归的计算出。这个步骤相当于给定了POSG在视野深度为时的含隐式状态的标准型博弈表示后,构建其视野深度为时对应表示的过程。
第二步裁剪被支配策略树的过程,类似单智能体的情况,当一个智能体i的策略树被移去而不会引起智能体i任何信念处评价值下降,该策略树便可以被裁剪掉。同标准型博弈一样,移去一个智能体的策略树会降低其他智能体的信念空间的维度,它可以重复执行直到没有任何智能体的任何策略树能被裁剪(不同的智能体排序方式可能会导致不同的策略树及值向量的结果,被支配策略消除过程这种顺序相关的特性也是博弈论研究的一个重点,此处不做讨论)。
基于搜索的MAA*算法
Multi-agent A是第一个完整的针对有限视野DEC-POMDP问题的最优搜索算法。该算法相对后向动态规划类算法在效率上有很大优势,并且可以被设计成anytime的工作方式。和其他搜索类算法一样,MAA*求解基于给定初始状态。.
类似A的搜索算法目前都已成功的使用在MDP及POMDP问题上,MAA则是对该算法的进-步扩展,使其可以应用在多智能体规划领域。MAA*假定
启发式搜索
一个有限视野POMDP问题的解可以被表示成决策树的形式,其中节点标注行动而弧标注观察。类似的,一个给定初始状态的t步DEC-POMDP问题可以表示成含有n个对应不同智能体的t层策略树的向量,供同步执行,并称其为策略向量。策略向量空间中的前向搜索可以被看成由t视野深度的策略向量增量构建t+1视野深度的策略向量,即对前者的叶子节点进行展开。
记为对应智能体的层策略树。记为一个分别对应个小同智能体的策略树向量,每-一个深度都为 。定义)为从状态开始执行策略$ \deltas_0$,有最优视野策略向量:
使用类似A*的best-first 的搜索策略,逐渐的构建出向量空间中策略向量。其中深度t处节点上对应的是问题的部分解,称作视野深度策略向量。搜索过程的每次迭代包括评价搜索树的叶子节点,选择最高评价值的节点并扩展。部分搜索树的一个例子如图所示:
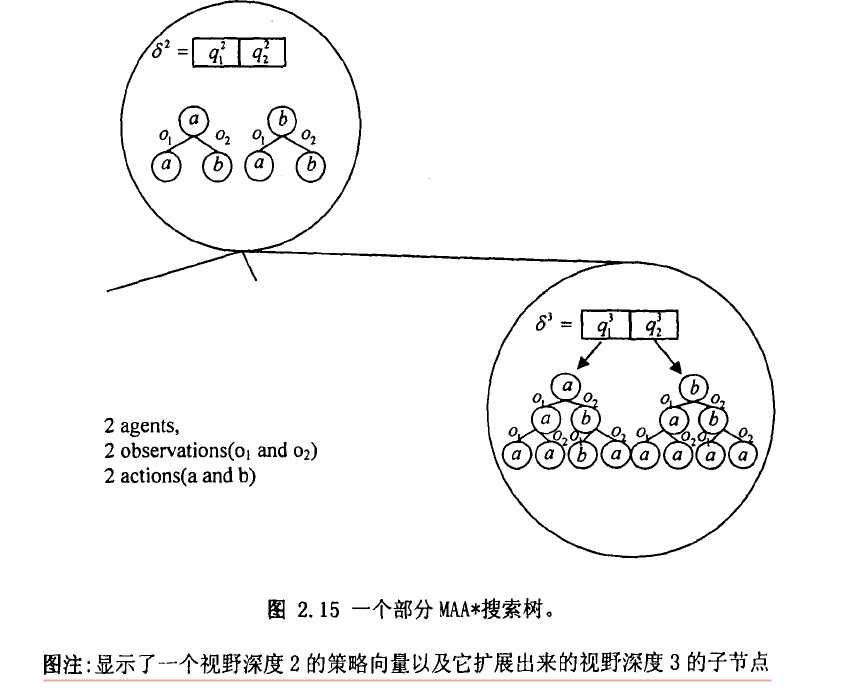
启发式搜索通常都是将评价函数分解为精确的部分解的评价以及其他部分的启发式估计。引入记为已经完成的任意深度t的策略向量,也就是深度为部分的策略树能够被连接在策略向量$ \delta\left{\delta^{t}, \Delta^{T-t}\right}T$的全部的策略向量,相应的值函数也可以分为两部分:.
按照启发式函数的一般设计方,定义上述函数的一个估计值
其中函数H为一个可接纳的启发式函数(admissibleheuristic),它总是实际值的一个乐观估计,即:
半马尔可夫决策过程SMDP
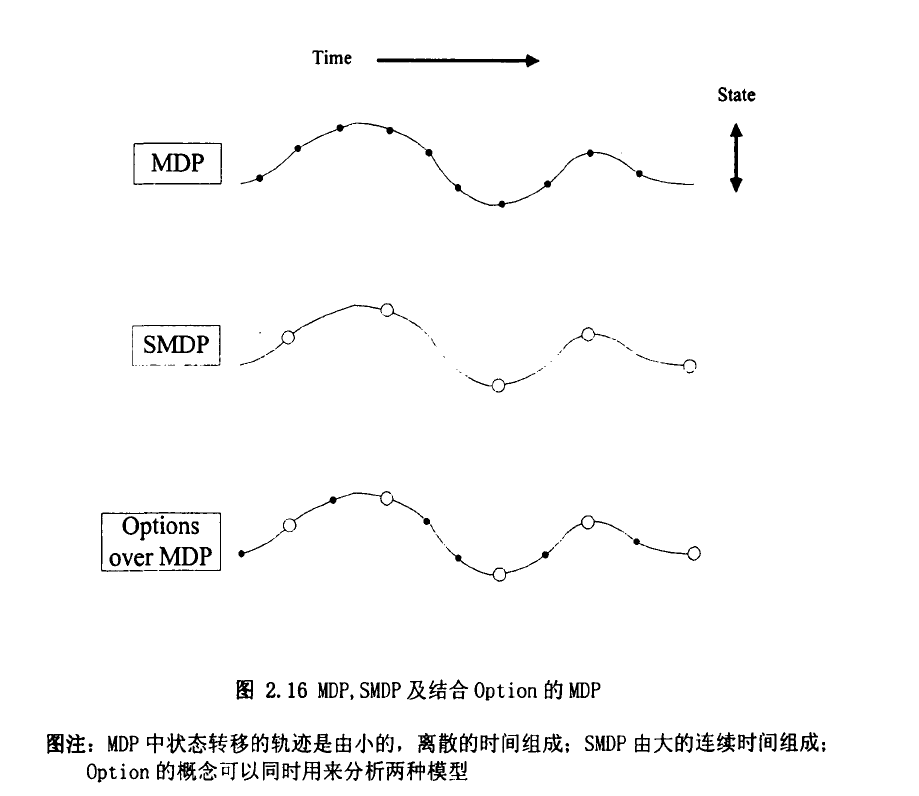
半马尔可夫决策过程一也称为非时齐马尔可夫决策过程,而前面所介绍的马尔可夫决策过程则是时齐过程。
所谓时齐指的是模型中所有的每步可选行动的执行时间是相同的及相邻状态之间转移的时间间隔一致。而非时齐马尔可夫决策过程则与此不同从行动开始到进入下个状态的时间间隔不一致甚至行动的延续周期还是一个时间上的概率分布。
从本质上讲,世界总是无限可分,半马尔可夫决策过程经过进一步时间上的一致的离散并对行动集合作以整理仍可以转化为一个马尔可夫过程。但半马尔可夫本身的存在意义在于它更接近现实中人类规划并解决问题的方式。人类规划问题的方式常常都是基于一些时延行动的过程,它们通常具有较大尺度的时间范围。
半马尔可夫决策过程的行动可以看成相应的潜在的马尔可夫决策过程中行动的多步组合,这里涉及到一个时间抽象的概念.。
MDP一般被认为不涉及时间抽象或时延行动,通常是基于离散的时间步数,一个单一的行动在时刻执行获得相应立即回报并影响状态转移进入下一个时刻.这里没有持续一段时期的过程行动的概念.因而,传统的方法无法利用某些情况下高层的时间抽象带来的简化与效率。
SMDP可以算是一类特殊的适用于建模具有连续时间离散事件性质的系统。Parr(1998)的。如前面所说,任何-一个SMDP都存在-一个潜在的MDP与之对应,而给定一个MDP也存在经由抽象转化为一个SMDP来处理的可能。Suttonetal(1999)最早研究了这种关系,并提出了Option 做为行动的- 一个替代概念。Option可以理解为选择的意思,本质上它指出智能体在一个决策过程中所要挑选的仅仅是一个选择,而不用再去区分这个选择到底是一个类似MDP中行动那样的原子动作,还是SMDP中那样的时延行为。所谓经抽象后的持续一个时间段的行为本质上也是由原子动作组成的,图2.16简单的说明了它们之间的联系。
Option
在MDP模型中加入Option 这一概念 即可构成一一个 SMDP来处理。Option是对MDP原子行动的一个扩展,使其加入了具有时延过程的行动。Option 由三部分组成:一个策略, -一个终止条件,以及一个初始集合.
一个Option 当且仅当时在状态是可用的。
如果Option被选择,则按照选择行动,直到Option根据随机终止。
具体来说,一个马尔可夫过程是按下面的流程进行的。
首先,行动根据选择并执行
此时Option或者以概率终止,或者继续,
然后继续根据确定,如此循环。
当终止时智能体再次有机会来选择另一个Option。
如此循环。当终止时智能体再次有机会来选择另一个。如此循环。当终止时智能体再次有机会来选择另一个。
MDP, Option以及SMDP之间的关系,为使用Option进行规划提供了基础。在MDP模型中加入Option后,需要相应引入一些新的定义。首先,行动集合换为Option集合,Option简记为。设原MDP问题中使用表示立即收益,使用表示状态转移函数,可以定义相应的执行Option至其结束后的期望收益,及基于Option的转移函数(描述时间的变量记入状态内),令表示在时刻在状态发起的事件,则有:
事实上,Option 记录的就是-一个子策略。目前在Option基础上做的研究工作的一个关键问题是怎样确定Option及怎么样由Option 来进行分等级的规划。而如何从一-个普通 MDP问题中抽象出合适Option集合是该理论更好应用的难点问题(Ravindran B, et al, 2003, 2007)。
Option理论展示了一种结合子策略以半马尔可夫过程的形式进行问题规划的思想,为综合使用上述模型在大规模多智能体系统中进行分层规划提供了基础
本文来自博客园,作者:{珇逖},转载请注明原文链接:https://www.cnblogs.com/zuti666/p/18092793



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律
2023-03-24 Docker 挖坑