飞机基础知识一 1.3二维平面飞机运动学模型

合集 - 飞飞机(33)

1.空战博弈编程实现——2 初探JSBSIM2024-03-242.空战博弈实现——3 gym自定义环境2024-03-243.空战博弈编程实现——gym+jsbsim2024-03-244.空战博弈编程实现2024-03-245.空战编程实现——6 强化学习与控制器2024-03-246.空战博弈编程实现7——将JSBSI和强化学习算法融合2024-03-247.博弈论与强化学习 算法 一 MinimaxQ, NashQ ,FFQ2022-11-208.博弈论与强化学习——基础1 扩展型博弈2022-11-209.飞机游戏二 空战可视化+强化学习2022-12-0710.gym——1自定义Gym环境并注册2022-12-0711.博弈论与强化学习实战——CFR算法——剪刀石头布2022-12-0612.博弈论与强化学习——— 基础2 马尔科夫博弈2022-11-2013.飞机游戏六 空战强化学习环境6.1DBML 6.1.1DBML 使用2022-12-0914.飞机游戏五 强化学习算法库2022-12-0815.分层强化学习32022-12-0816.飞机游戏三仿真软件 3.2Airsim介绍2022-12-0817.强化学习与控制器2022-12-0818.飞机游戏四 飞机作战场景2022-12-0819.飞机游戏三仿真软件 3.1JSBSim介绍2022-12-0820.飞机游戏 一 飞行基础知识　１.１概念介绍2022-12-0821.空战编程实现1——小雅2024-03-2422.分层强化学习2024-03-2423.问题建模2024-03-2424.多智能体理论2024-03-2425.马尔可夫决策理论2024-03-24

26.飞机基础知识一 1.3二维平面飞机运动学模型2023-03-25

27.飞机游戏六 空战环境 6.1 DBRML 6.1.5 动作空间设置2023-03-2328.飞行基础知识一　１.２飞机的三自由度方程2023-03-2329.中远距空战对战场景2023-03-2030.飞机游戏六空战强化学习环境6.1DBML 6.1.4 DBML+强化学习算法使用2023-02-1431.飞机游戏六空战强化学习环境6.1DBML 6.1.3 DBML+强化学习算法使用2022-12-1132.飞机游戏三仿真软件 3.3 Dogfight介绍 2022-12-1033.飞机游戏六空战强化学习环境 6.1DBML 6.1.2源码阅读与分析2022-12-10

收起

飞机基础知识一 1.3二维平面飞机运动学模型

目录

• 飞机基础知识一 1.3二维平面飞机运动学模型
  • 运动学方程
  • 程序实现
    • 完整代码
    • 效果

运动学方程

在二维平面上

将飞机视为一个质点

\[\begin{aligned} & \frac{d x}{d t}=v \cos \psi \\ & \frac{d y}{d t}=v \sin \psi \\ & \frac{d v}{d t}= a \\ & \frac{d \psi}{d t}= \omega \\ \end{aligned} \]

状态量为 位置 x ，y , 速率 v 速度与x轴的夹角 \(\theta\)

控制量为 加速度大小 \(a\) 和 角加速度大小 \(\omega\)

程序实现

给定初始状态

二维空间坐标值、飞行速率、与x轴夹角

\[x,y,v,\theta \]

state = [x,y,v,theta]

输入 ： 控制量 加速度 和 角加速度

\[a, \omega \]

control = [a , moega]

代码返回： 下一时间（一个仿真步长）的状态量

完整代码

# -*- coding: utf-8 -*-

"""
@author     : zuti
@software   : PyCharm
@file       : 2_run_func.py
@time       : 2023/3/25 14:58
@desc       ：

"""

import matplotlib.pyplot as plt
import numpy as np



plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams.update({'font.size': 12})

# 初始姿态
init_velocity, init_theta  = 100., np.pi/2
init_x, init_y = 0., 0.  # 初始位置

# todo 两个控制量
a = 5.  #单位  m/s2
omega = 1   #单位 rad/s2

state = [init_x, init_y,  init_velocity, init_theta]
control = [a,omega]

time = 1  # 秒 总时间
n = 10  # 仿真步数
t = np.linspace(0, time, n)  # 仿真步长

def update_position(state, control, time=1, n=100):
    """

    :param state:  初始状态
    :param control: 控制量
    :param time:   仿真时长
    :param n: 仿真步数
    :return:
    """
    t = np.linspace(0, time, n)  # 仿真步长
    dt = t[1] - t[0]
    state_list = np.zeros((n, 4))  # 轨迹长度
    state_list[0] = state  # 轨迹列表第一个元素为初始状态
    x,y,velocity, theta = state_list[0]

    for k in range(1, n):

        a  =   control[0]
        omega = control[1]

        velocity = velocity +   a * dt
        theta= theta+ omega * dt


        dx = velocity * np.cos(theta) * dt
        dy = velocity * np.sin(theta) * dt


        x = x + dx
        state_list[k, 0] = x
        y = y + dy
        state_list[k, 1] = y


        state_list[k, 2] = velocity
        state_list[k, 3] =  theta

    return state_list

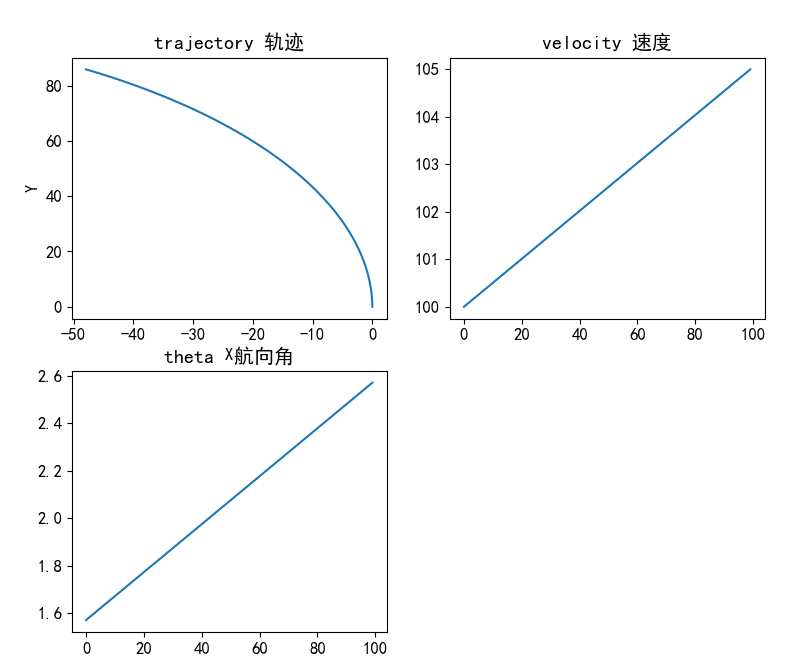
#测试运动学方程
state_list = update_position(state,control)
print(f'轨迹 {state_list}')
#绘制图像
fig = plt.figure()
ax1 = fig.add_subplot(221)
ax1.plot(state_list[:, 0], state_list[:, 1])
ax1.set_title('trajectory 轨迹')
ax1.set_xlabel('X')
ax1.set_ylabel('Y')


ax2 = fig.add_subplot(222)
ax2.plot(state_list[:,2])
ax2.set_title('velocity 速度')


ax3 = fig.add_subplot(223)
ax3.plot(state_list[:,3])
ax3.set_title('theta  航向角')

#plt.savefig('test.jpg')
plt.show()

效果