分层强化学习3

分层强化学习

目录

• 分层强化学习
  • Option
    • 在MDP模型中加入Option
  • HAM （Hierarchical Abstract Machines）
  • MAXQ
• 自动分层研究
• 仿真实验
  • 1 多出租车问题
  • 2 垃圾收集
  • 3 多机器人足球
  • 4 多机器人搜救

HRL方法通过引入抽象( Abstraction)机制来实现状态空间的降维，将学习任务分解到抽象内部和抽象之间不同层次上来分别实现,使得每层上的任务仅需在低维空间中进行。因此，建立在合理抽象机制上的HRL能极大减少存储空间和计算量，加快学习速度，有利于解决“维度灾难"问题。典型的HRL方法有Parr提出的HAM、Dietterich提 出的MAXQ、Sutton提 出的Option和Hengst提出的HEXQ等。

Option

SMDP可以算是一类特殊的适用于建模具有连续时间离散事件性质的系统。Parr(1998)的。如前面所说，任何-一个SMDP都存在-一个潜在的MDP与之对应，而给定一个MDP也存在经由抽象转化为一个SMDP来处理的可能。Suttonetal(1999)最早研究了这种关系，并提出了Option 做为行动的- 一个替代概念。Option可以理解为选择的意思，本质上它指出智能体在一个决策过程中所要挑选的仅仅是一个选择，而不用再去区分这个选择到底是一个类似MDP中行动那样的原子动作，还是SMDP中那样的时延行为。所谓经抽象后的持续一个时间段的行为本质上也是由原子动作组成的，图2.16简单的说明了它们之间的联系。

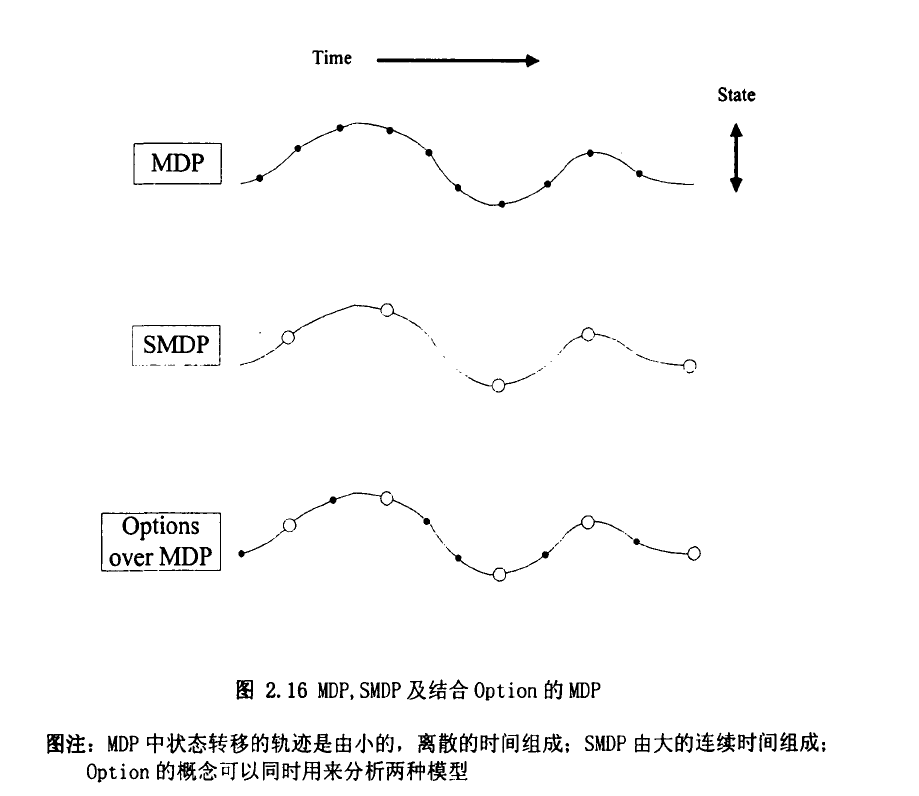
在MDP模型中加入Option

Option是对MDP原子行动的一个扩展，使其加入了具有时延过程的行动。

Option 由三部分组成:

• 一个策略\(π:S\times A→[0,1]\)，

• 一个终止条件\(β:S^*→[0,1]\)​,在状态\(s'\)按照概率\(\beta(s')\)终止Option。通常，将Option任务的子目标状态点\(s_{t+1}\)的终止条件设定为\(\beta(s_{t+1})=1\)

• 一个初始集合$ \mathcal{I} \subseteq S \(。当且仅当\)s_t \in \mathcal{I}\(时,集，Option\)\langle \mathcal{I}, \pi, \beta\rangle\(才会按照它的内部策略开始执行。\)\mathcal{I}$ 必须包含且只可以包含该Option可能探索到的所有状态:

一个Option \(\langle \mathcal{I}, \pi, \beta\rangle\) 当且仅当\(s_t \in \mathcal{I}\)时在状态\(s_t\)是可用的。如果Option被选择，则按照\(π\)选择行动，直到Option根据\(β\)随机终止。

具体来说,一个马尔可夫过程是按下面的流程进行的。

​ 首先,行动\(a_t\)根据\(\pi(s_t,\cdot)\)选择并执行

​ 此时Option或者以概率\(β\)终止，或者继续，

​ 然后继续根据\(\pi(s_t,\cdot)\)确定\(a_{t+1}\),

如此循环，当终止时智能体再次有机会来选择另一个Option。

MDP, Option以及SMDP之间的关系，为使用Option进行规划提供了基础。

在MDP上叠加Semi-Markov-Option，便可以形成SMDP。若把所有Option均拓展到基本动作层，则策略\(\pi\)便可确定马尔可夫决策过程中的一个常规策略，并称其为与\(\pi\)对应的平坦策略，标记为\(flat(\pi)\)。

在MDP模型中加入Option后，将所有Option O需要相应引入一些新的定义。

首先，行动集合换为Option集合，Option简记为\(o\)。设原MDP问题中使用\(r_s^a\)表示立即收益，使用\(p_{ss'}^a\)表示状态转移函数，可以定义相应的执行Option至其结束后的期望收益\(r_s^a\)，及基于Option的转移函数\(p^o_{ss'}\)(描述时间的变量记入状态内),

令\(ε(o,s,t)\)表示在时刻\(t，o\)在状态\(s\)发起的事件，则有:

\[\begin{equation} \begin{gathered} r_{s}^{o}=E\left\{r_{t+1}+\gamma r_{t+2}+\cdots+\gamma^{k-1} r_{t+k} \mid \varepsilon(o, s, t)\right\} \\ p_{s s^{+}}^{o}=\sum_{k=1}^{\infty} p\left(s^{\prime}, k\right) \gamma^{k} \end{gathered} \end{equation} \]

在策略\(\pi\)下，Option中状态\(s\)的状态价值函数为：

\[\begin{equation} V^{\pi}(s)=E\left\{r_{t}+\gamma r_{i+1}+\cdots+\gamma^{\tau-1} r_{t+\tau-1}+\gamma^{\tau} V^{\pi}\left(s_{t+\tau}\right) \mid \varepsilon(\pi, s . t)\right\} \end{equation} \]

其中\(\varepsilon (\pi, s . t)\)表示在1时刻时，Option \(\pi\)在状态\(s\)下被启动。
相应的Option o中状态\(s\)的值函数的最优方程分别为:

\[\begin{equation} V_{0}^{*}(s)=\max _{u \in O_{s}}\left\{R(s, o)+\sum_{s^{\prime}} P\left(s^{\prime} \mid s, o\right) V_{O}^{*}\left(s^{\prime}\right)\right\} \end{equation} \]

和

\[\begin{equation} Q_{o}^{*}(s, o)=R(s, o)+\sum_{s^{\prime}} P\left(s^{\prime} \mid s, o\right) \max \underset{o^{\prime} \in O_{s}^{\prime}}{Q_{0}^{*}}\left(s^{\prime}, o^{\prime}\right) \end{equation} \]

定义在Option上的标准Q-学习的值函数迭代公式为:

\[\begin{equation} Q_{k+1}(s . o)=\left(1-\alpha_{k}\right) Q_{k}(s, o)+\alpha_{k}\left[r+\gamma^{\tau} \max \underset{\sigma^{\prime} \in Q_{i}}{Q_{i}}\left(s^{\prime}, o^{\prime}\right)\right] \end{equation} \]

​ 可以证明当满足标准Q-学习的收敛条件时,基于Option的Q-学习算法可以按照概率1收敛到\(Q_{o}^{*}\)。

综上可知，Option算法的任务分层过程是一个在状态空间上不断发现子目标，并基于这些子目标构建Options的过程。随着该过程的不断进行，系统的决.策空间就会相应增长，新构建的Option会被添加到任务的决策空间中，因此，构建合理的Option可以有效地避免智能体在动态环境中的盲目探索，大大加快系统的学习速度。

​ 事实上，Option 记录的就是一个子策略。目前在Option基础上做的研究工作的一个关键问题是怎样确定Option及怎么样由Option 来进行分等级的规划。而如何从一个普通 MDP问题中抽象出合适Option集合是该理论更好应用的难点问题(Ravindran B, et al, 2003, 2007)。

HAM （Hierarchical Abstract Machines）

Hierarchical Abstract Machines - YouTube

Parr提出了一种典型的分层强化学习方法HAM ( Hierarchical Abstract Machines) [61],它把各个子任务抽象为一个基于马尔可夫决策过程建立的随机有限状态机。

有限状态机参考笔记

令\(M=<S,A,P,R>\)表示有限马尔可夫决策过程，其中，\(S\)为状态集，\(A\)为可执行的动作集，\(P:S\times A→PD(S)\)表示状态转移概率函数，\(R\)表示奖赏函数。

用随机有限状态机的集合\(H =\{H_i\}\)来表示HAM的策略，其中，\(H_i\)包含状态集$ S_i\(,、随机函数\)φ_i:S→S_i\(, (它用于设定\)H_i\(的初始状态)以及随机状态转移概率函数\)δ_i\(,即\)H_i=<S_i,δ_i,φ_i>$。

随机有限状态机H,包含四种类型的内部状态: \(action\)， \(choice\),$ call\(和\)stop$。

• \(action\)类状态能够基于\(H_i\)的当前状态和\(M\)产生一个\(M\)的动作，即在\(t\)时刻时产生一个动作\(a=π(m_t',s_t)∈A_{s_t}\)。其中，\(m_t'\)是\(H_i\)的当前状态，$s_t \(是\)M$的当前状态;
• \(choice\)类状态随机选择\(H_i\)的下一状态，并且需要在学习过程中优化\(H_i\)的策略;
• \(call\)类状态会暂停当前运行的\(H_i\)，而去启动执行另一个\(H_j\)，$j \(是\)m_j'\(的函数，当它被调用时，将\)H_j\(的状态设定为\)φ_j(s_i)$
• \(stop\)状态停止执行当前的随机有限状态机\(H_i\)，且返回到调用它的随机有限状态机。

只有\(action\)类，接受一个状态输入，输出一个动作;其他的类都没有输出；

$call $类是控制,建立了一个分层体系，产生一个调用图（或者说栈堆）

一般来说，\(H_i\)的子目标被定义为\(stop\)类状态。在随机有限状态机的内部状态进行转换的同时，有限MDPM接受\(action\)类状态生成的动作，并按照其自身的状态转移概率转移到下一状态，同时获得环境的立即奖赏。但如果\(t\)时刻没有动作生成，则有限马尔可夫决策过程M会保持在当前状态.

MAXQ

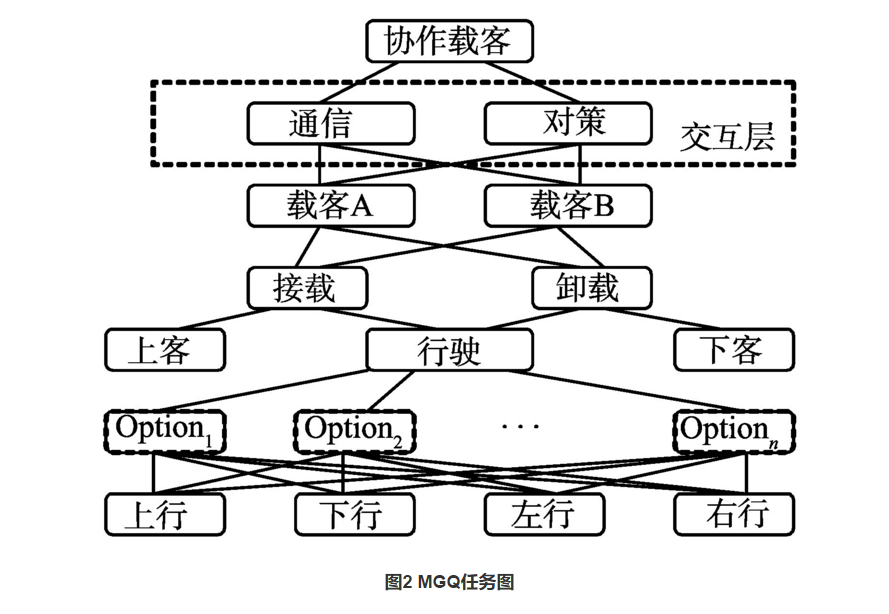
MAXQ方法将整个学习任务W分解为子任务集\({W_0,W_1,\cdots,W_n}\)，并将策略\(π\)分解为策略的集合\({\pi_0,\pi_1，\cdots,π_n}\)，其中，\(π_i\),是子任务\(W_i\)的策略。进行学习的任务就是确定每个子任务\(W_i\)的最优策略\(π^* (i,s)\)。所有子任务形成了以\(W_0\)为根节点的任务分层结构，即任务图。
从任务图可以看出各子任务之间的关系，上层子任务的完成依赖其下层子任务的实现，且上层子任务只能从它的子节点中选择执行子任务,因此对上层的策略空间进行了约束，有效缩小了各子任务的决策空间，显著加快了系统的学习速度。
由于解决了根任务W。也就解决整个学习任务W，因此为了解决W，需要依次选择调用基本动作或者其它子任务。任务图中各子节点的顺序是任意的，即任务图只约束了每层中可以选择的动作，因此，学习时需要高层控制器根据其采用的策略选择动作。

MAXQ中的每个子任务\(W_i\)可以由三元组\(<π_i,T_i,R_i>\)构成。

• 智能体从子任务\(W_i\)的子节点中，根据策略\(π_i\),选择执行子任务( 基本动作或复合动作);

• 终止谓词\(T_i\)，将整个状态集划分为:

  • 引起\(W_i\)结束的终止状态集\(F_i\)
  • 策略\(π_i\)可执行的活动.状态集\(S_i\)

• \(R_i\) 是奖赏函数。

投影值函数\(V^{\pi}(i,s)\)给出了子任务\(W_i\)中状态\(s\)的期望回报值。对每个子任务\(W_i\),\(S_i\),为其状态集，\(W_i\) 对应的所有子节点(子任务)为其动作集，\(P_i(s',\tau|s,a)\)表示子任务\(W_i\)中，在状态\(s\)执行动作\(a\)导致环境状态转移到\(s'\)的状态转移概率。对任意状态\(s∈S\)，\(W_i\)中执行动作\(a\)获得的立即奖赏为\(R_i(s,a)=V(a,s)\)。与子任务\(W_i\) 对应的状态的值函数方程为:

\[\begin{equation} V(i, s)=V(a, s)+\sum_{s^{\prime}, t} P_{l}\left(s^{\prime}, \tau \mid s, a\right) \gamma^{\tau} V\left(i, s^{\prime}\right) \end{equation} \]

其中，\(V(i.s')\) 是由状态\(s'\) (子任务\(a\)结束时对应的状态)开始完成子任务\(W_i\)的期望回报值。

子任务\(W_i\)中，状态-动作对的值函数定义为:

\[\begin{equation} Q(i, s, a)=V(a, s)+\sum_{s^{\prime}, \tau} P_{1}\left(s^{\prime}, \tau \mid s, a\right) \gamma^{\tau} \max Q\left(i, s^{\prime}, \pi\left(s^{\prime}\right)\right) \end{equation} \]

其中，式(2-26)的第二项称为完成函数\(C( i,s,a)\)，即:

\[\begin{equation} C(i, s, a)=\sum_{s^{\prime} \tau} P\left(s^{\prime}, \tau \mid s, a\right) \gamma^{\tau} \max Q\left(i, s^{\prime}, \pi\left(s^{\prime}\right)\right) \end{equation} \]

上式给出了子任务a终止后完成子任务W,的期望回报值。

因此,通过MAXQ值函数分解，状态-动作对的值函数可以划分为立即奖赏\(V(a,s)\)和完成函数\(C( i,s,a\))两部分，

\[\begin{equation} Q(i, s, a)=V(a, s)+C(i, s, a) \end{equation} \]

若已知MDP的分层策略π，假定根任务\(W_0\)的策略选择执行子任务\(a_1\)，\(a_1\)的策略选择执行子任务\(a_2\),这样依次进行选择,直到\(a_{n-1}\) 的策略选择了基本动作\(a_n\),，则根任务\(W_0\)中状态\(s\)的投影值\(V^{\pi}(0,s)\)可以分解为:

\[\begin{equation} V^{\pi}(0, s)=V^{\pi}\left(a_{n}, s\right)+C^{\pi}\left(a_{n-1}, s, a_{n}\right)+\cdots+C^{\pi}\left(a_{1}, s, a_{2}\right)+C^{\pi}\left(0, s, a_{1}\right) \end{equation} \]

其中

\[\begin{equation} V^{\tau}\left(a_{n^{n}}, s\right)=\sum_{s^{\prime}} P\left(s^{\prime} \mid s, a_{n}\right) R\left(s^{\prime} \mid s, a_{n}\right) \end{equation} \]

按照Dietterich的定义，当每个子策略\(π_i\)均为\(W_i\)的最优策略时，分层策略\(π=\{\pi_0,π_1,\cdots,π_n\}\)即为任务\(W\)的递归最优策略。Ditterich证明了若智能体执行有序GLIE (Greedy in the Limit with Infinite Exploration) [941策略， 步长参数根据随机逼近条件收敛到0，且立即奖赏有界时，MAXQ_Q算法能够收敛。

自动分层研究

仿真实验

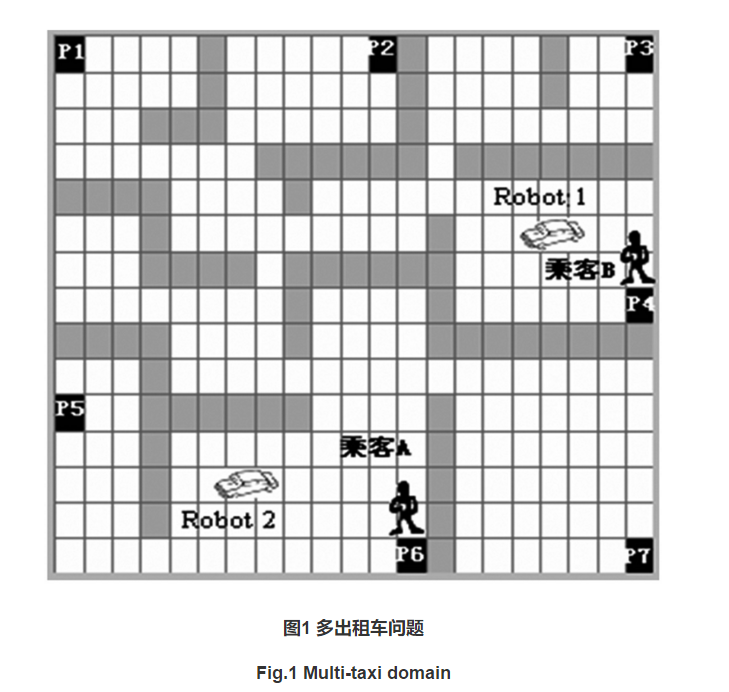
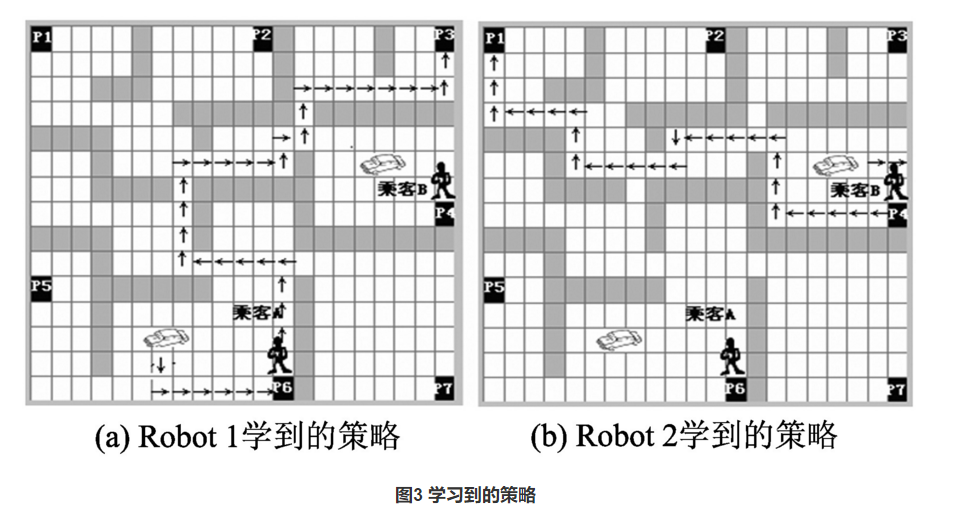
1 多出租车问题

以HRL研究中常采用的出租车问题(taxi domain)为任务背景。但以往的出租车问题主要是为单体分层强化学习设计的,本文将该任务拓展到更一般的情况,即多个乘客、多辆出租车(以Robot表示)。拓展后的出租车问题与多机器人搬运、垃圾收集、巡逻等问题是同构的。

2 垃圾收集

3 多机器人足球

4 多机器人搜救